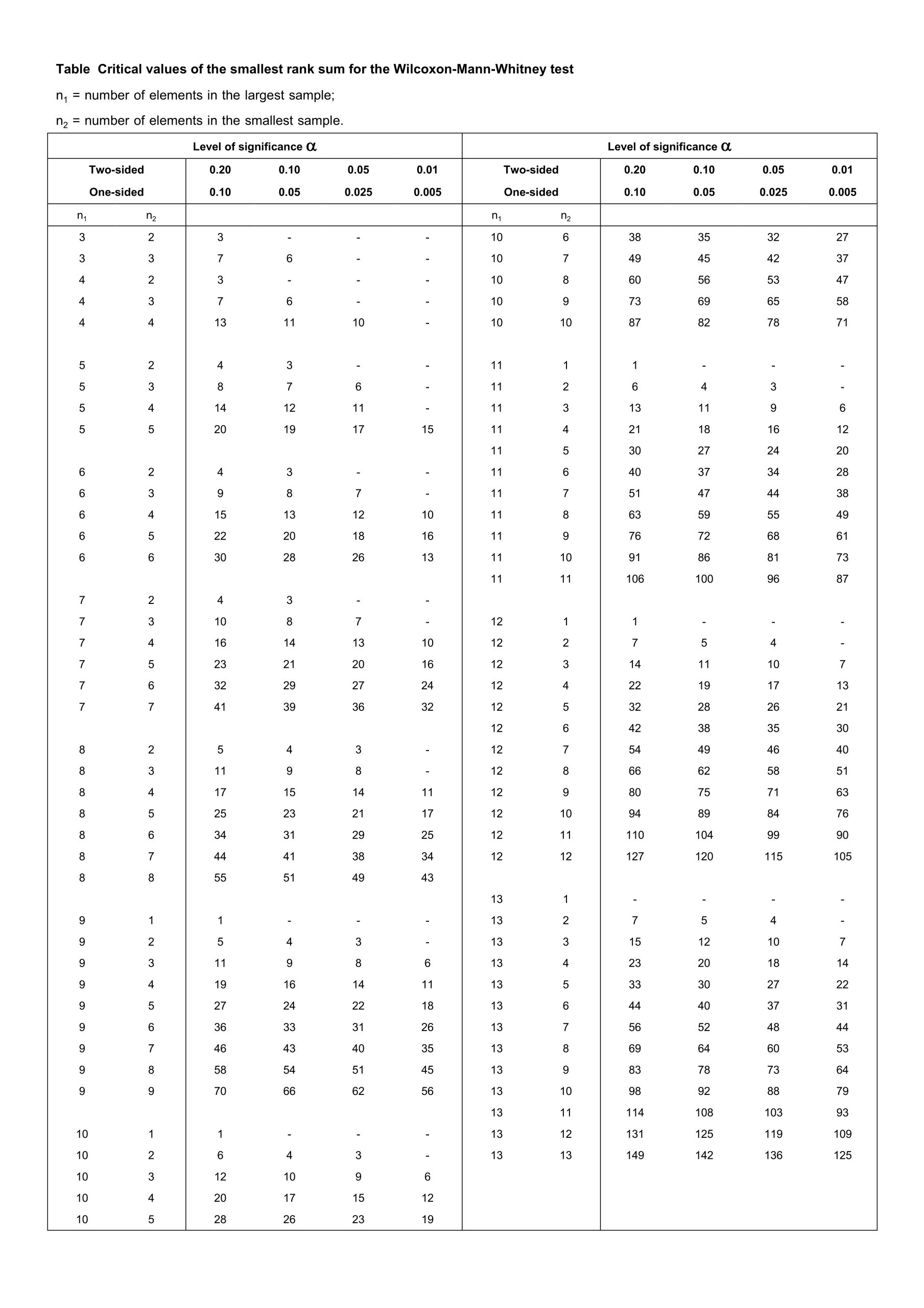
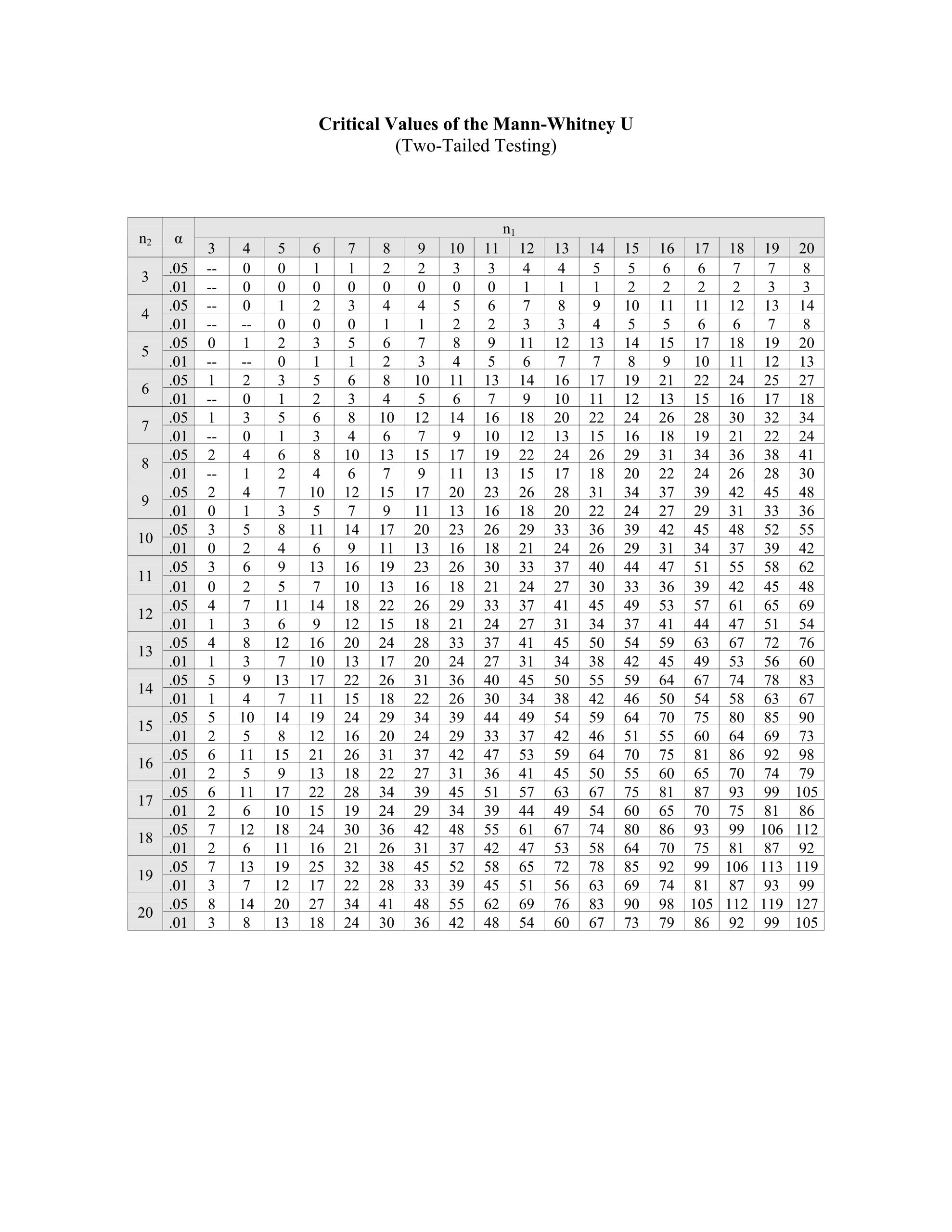
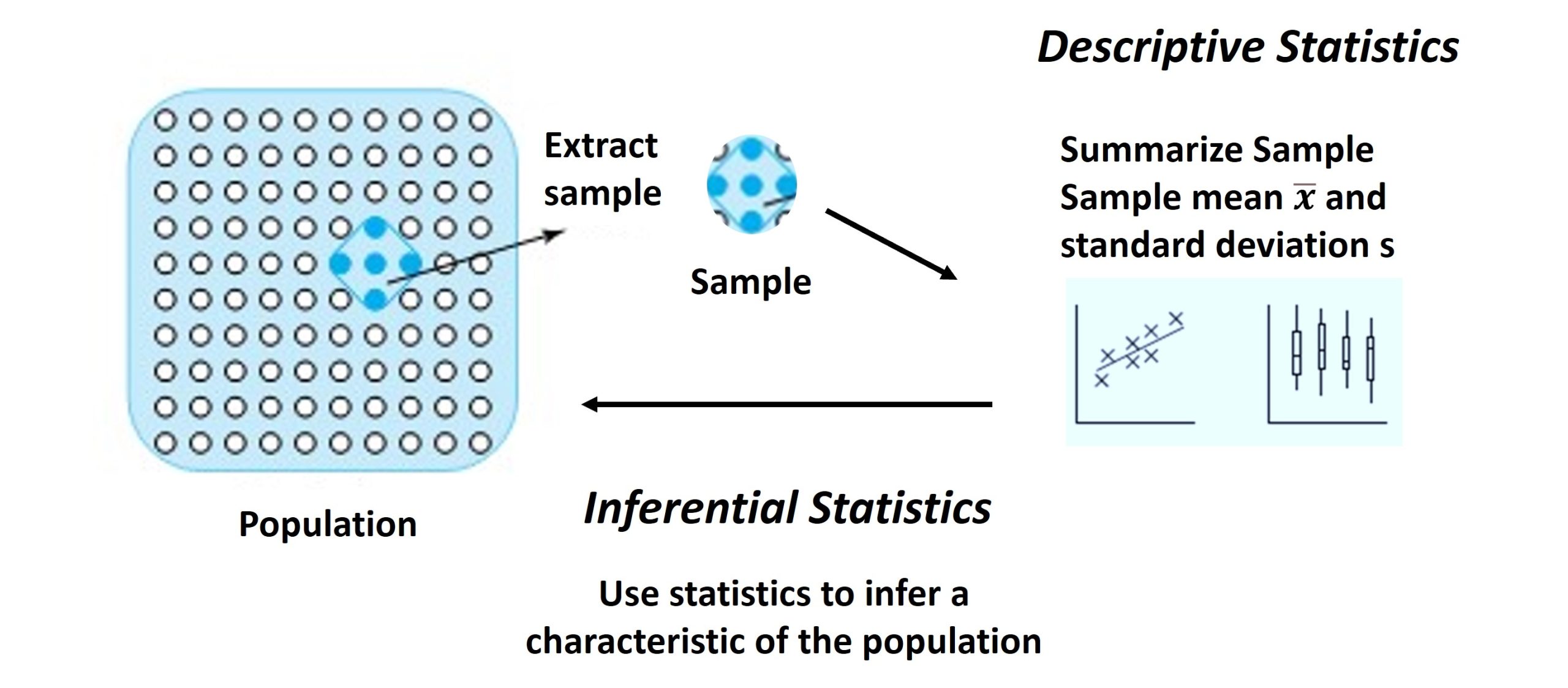
Large-Sample Confidence Intervals for a Mean
Many important engineering applications of statistics fit the following standard mold. Values for parameters of a data-generating process are unknown. Based on data, the object is
- identify an interval of values likely to contain an unknown parameter (or a function of one or more parameters) and
- quantify “how likely” the interval is to cover the correct value.
.
For example, a piece of equipment that dispenses baby food into jars might produce an unknown mean fill level, µ. Determining a data-based interval likely to contain µ and an evaluation of the reliability of the interval might be important. Or a machine that puts threads on U-bolts might have an inherent variation in thread lengths, describable in terms of a standard deviation, σ . The point of data collection might then be to produce an interval of likely values for σ , together with a statement of how reliable the interval is. Or two different methods of running a pelletizing machine might have different unknown propensities to produce defective pellets, (say, p1 and p2). A data-based interval for p1 − p2 , together with an associated statement of reliability, might be needed
.
DEFINITION 5.1.1.1 Confidence Interval
A confidence interval for a parameter (or function of one or more parameters) is a data-based interval of numbers thought likely to contain the parameter (or function of one or more parameters) possessing a stated probability-based confidence or reliability.
This section discusses how basic probability facts lead to simple large-sample formulas for confidence intervals for a mean, µ. The unusual case where the standard deviation σ is known is treated first. Then parallel reasoning produces a formula for the much more common situation where σ is not known. The section closes with discussions of three practical issues in the application of confidence intervals.
A Large-n Confidence Interval for  involving
involving 
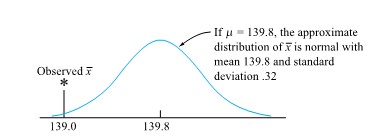
The final example in Chapter 4.2.2.4 involved a physically stable filling process known to have a net weight standard deviation of σ = 1.6 g. Since, for large n,thesample mean of iid random variables is approximately normal, the final example of Chapter 4.2.4 argued that for n = 47 and
 = the sample mean net fill weight of 47 jars filled by the process (g)
= the sample mean net fill weight of 47 jars filled by the process (g)
here is an approximately 80% chance that  is within .3 gram of µ. This fact is pictured again in Figure 5.1.1.1.
is within .3 gram of µ. This fact is pictured again in Figure 5.1.1.1.

Figure 5.1.1.1 Approximate probability distribution for x¯ based on n = 47
Notation ConventionsWe need to interrupt for a moment to discuss notation. In Part 4, capital letters were carefully used as symbols for random variables and corresponding lowercase letters for their possible or observed values. But here a lowercase symbol,  has been used for the sample mean random variable. This is fairly standard statistical usage, and it is in keeping with the kind of convention used in earlier Parts. We are thus going to now abandon strict adherence to the capitalization convention introduced in Chapter 4. Random variables will often be symbolized using lowercase letters and the same symbols used for their observed values. The Chapter 4 capitalization convention is especially helpful in learning the basics of probability. But once those basics are mastered, it is common to abuse notation and to determine from context whether a random variable or its observed value is being discussed.
has been used for the sample mean random variable. This is fairly standard statistical usage, and it is in keeping with the kind of convention used in earlier Parts. We are thus going to now abandon strict adherence to the capitalization convention introduced in Chapter 4. Random variables will often be symbolized using lowercase letters and the same symbols used for their observed values. The Chapter 4 capitalization convention is especially helpful in learning the basics of probability. But once those basics are mastered, it is common to abuse notation and to determine from context whether a random variable or its observed value is being discussed.
.
The most common way of thinking about a graphic like Figure 5.1.1.1 is to think of the possibility that
5.1.1.1 
in terms of whether or not  falls in an interval of length 2(.3) = .6 centered at µ. But the equivalent is to consider whether or not an interval of length .6 centered at
falls in an interval of length 2(.3) = .6 centered at µ. But the equivalent is to consider whether or not an interval of length .6 centered at  falls on top of µ. Algebraically, inequality (5.1.1.1) is equivalent to
falls on top of µ. Algebraically, inequality (5.1.1.1) is equivalent to
5.1.1.2 
which shifts attention to this second way of thinking. The fact that expression (5.1.1.2) has about an 80% chance of holding true anytime a sample of 47 fill weights is taken suggests that the random interval
5.1.1.3 
can be used as a confidence interval for µ, with 80% associated reliability or confidence.
Suppose a sample of n = 47 jars produces  = 138.2 g. Then expression (5.1.1.3) suggests that the interval with endpoints
= 138.2 g. Then expression (5.1.1.3) suggests that the interval with endpoints
138.2 g  .3 g
.3 g
(i.e., the interval from 137.9 g to 138.5 g) be used as an 80% confidence interval for the process mean fill weight.
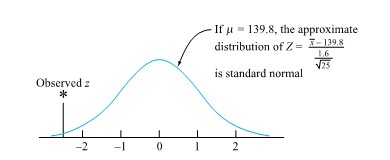
It is not hard to generalize the logic that led to expression (5.1.1.3). Anytime an iid model is appropriate for the elements of a large sample, the central limit theorem implies that the sample mean  is approximately normal with mean µ and standard deviation σ/√n. Then, if for p >.5, z is the p quantile of the standard normal distribution, the probability that
is approximately normal with mean µ and standard deviation σ/√n. Then, if for p >.5, z is the p quantile of the standard normal distribution, the probability that
5.1.1.4 
is approximately 1 − 2(1 − p). But inequality (5.1.1.4) can be rewritten as
5.1.1.5 
and thought of as the eventuality that the random interval with endpoints
EXPRESSION 5.1.1.6 Large-Sample Known  Confidence Limits for
Confidence Limits for 

brackets the unknown µ. So an interval with endpoints (5.1.1.6) is an approximate confidence interval for µ (with confidence level 1 − 2(1 − p)).
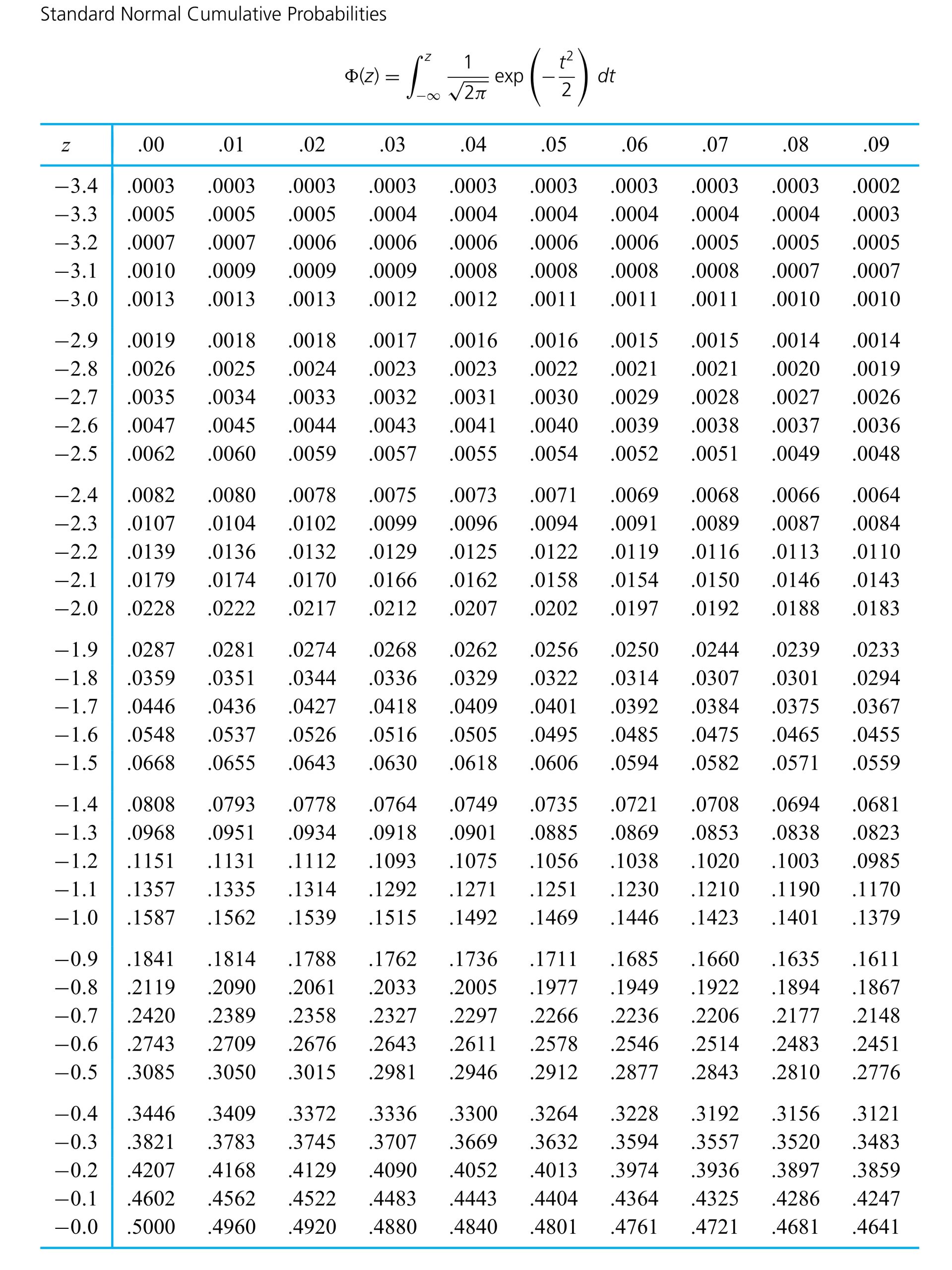
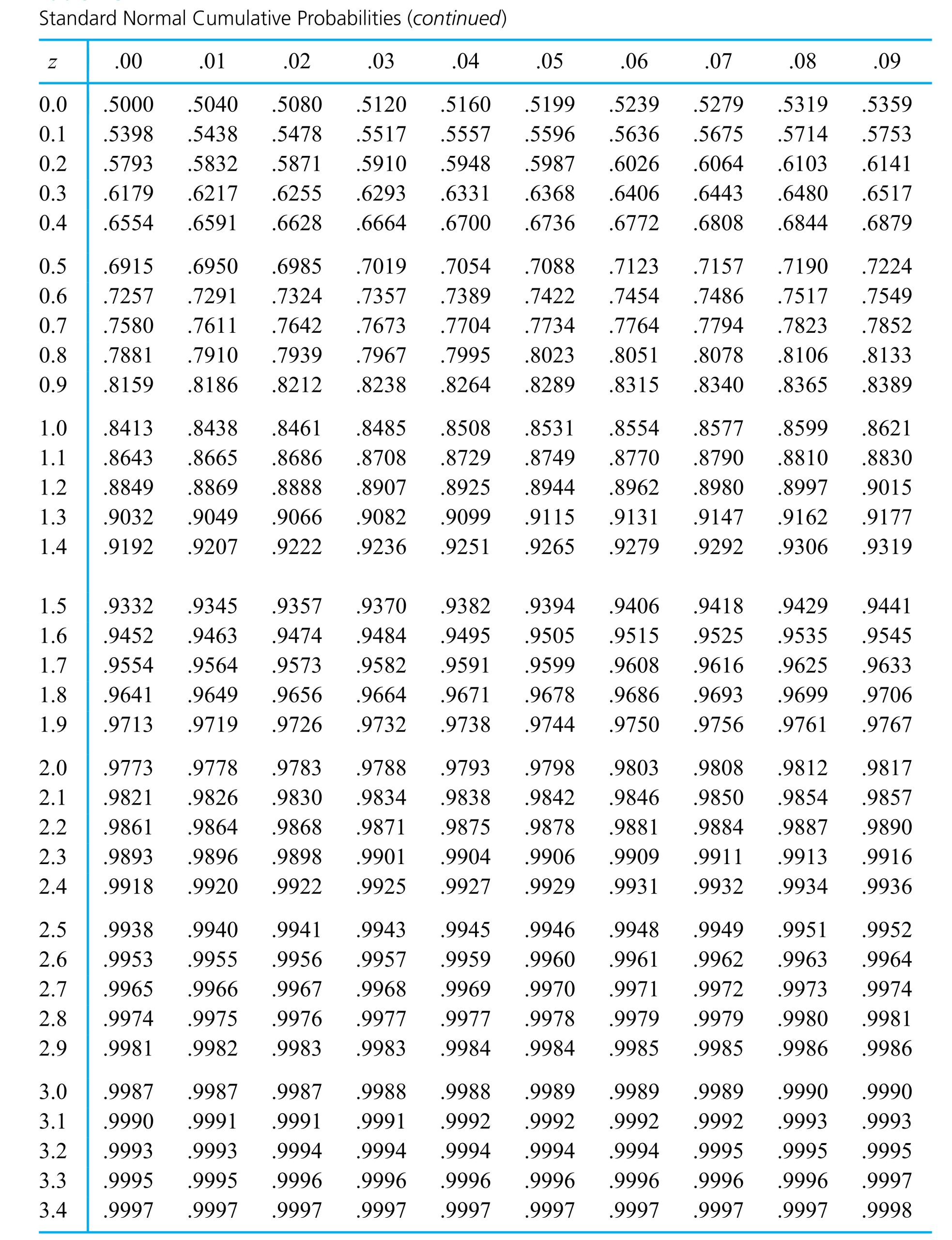
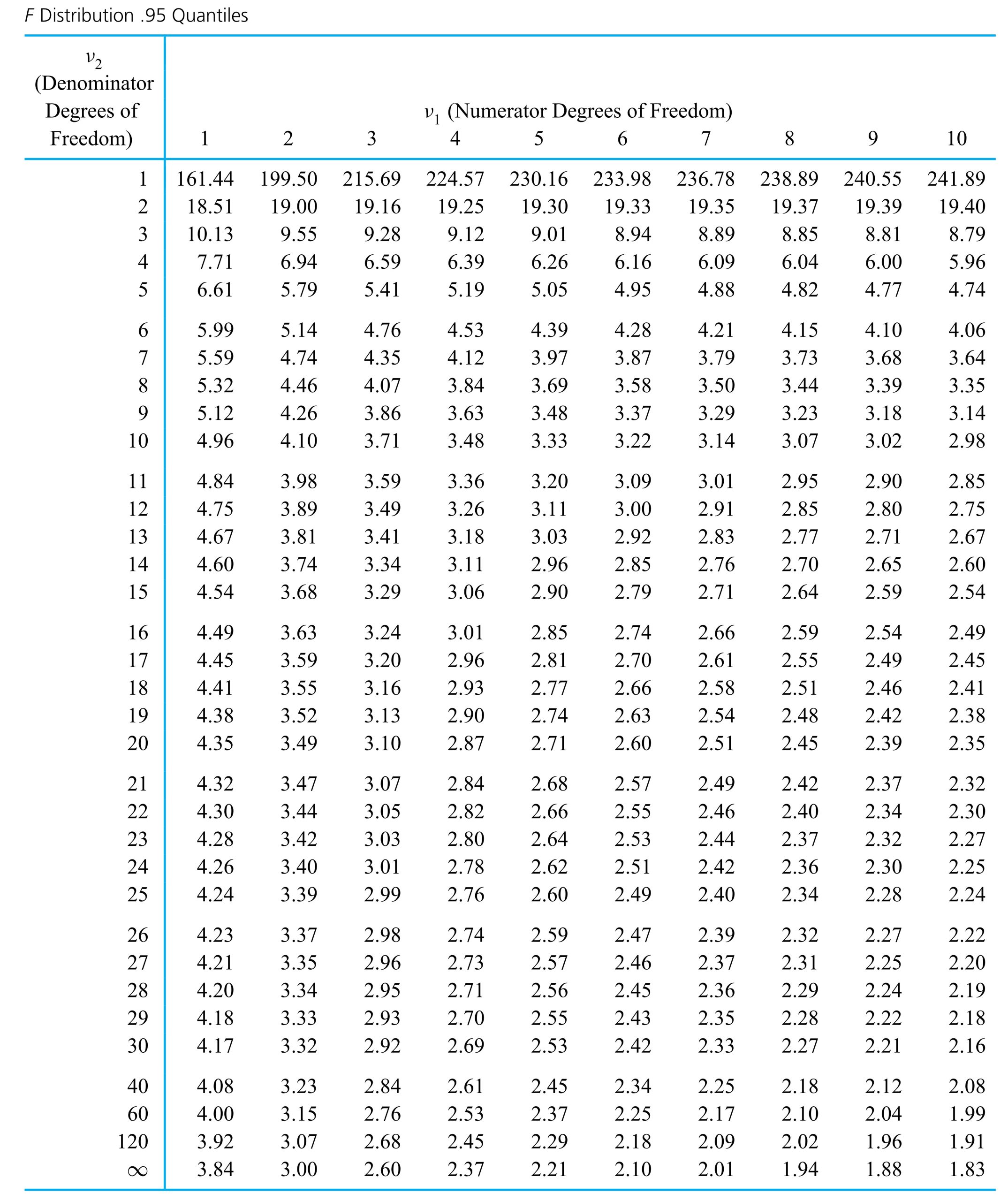
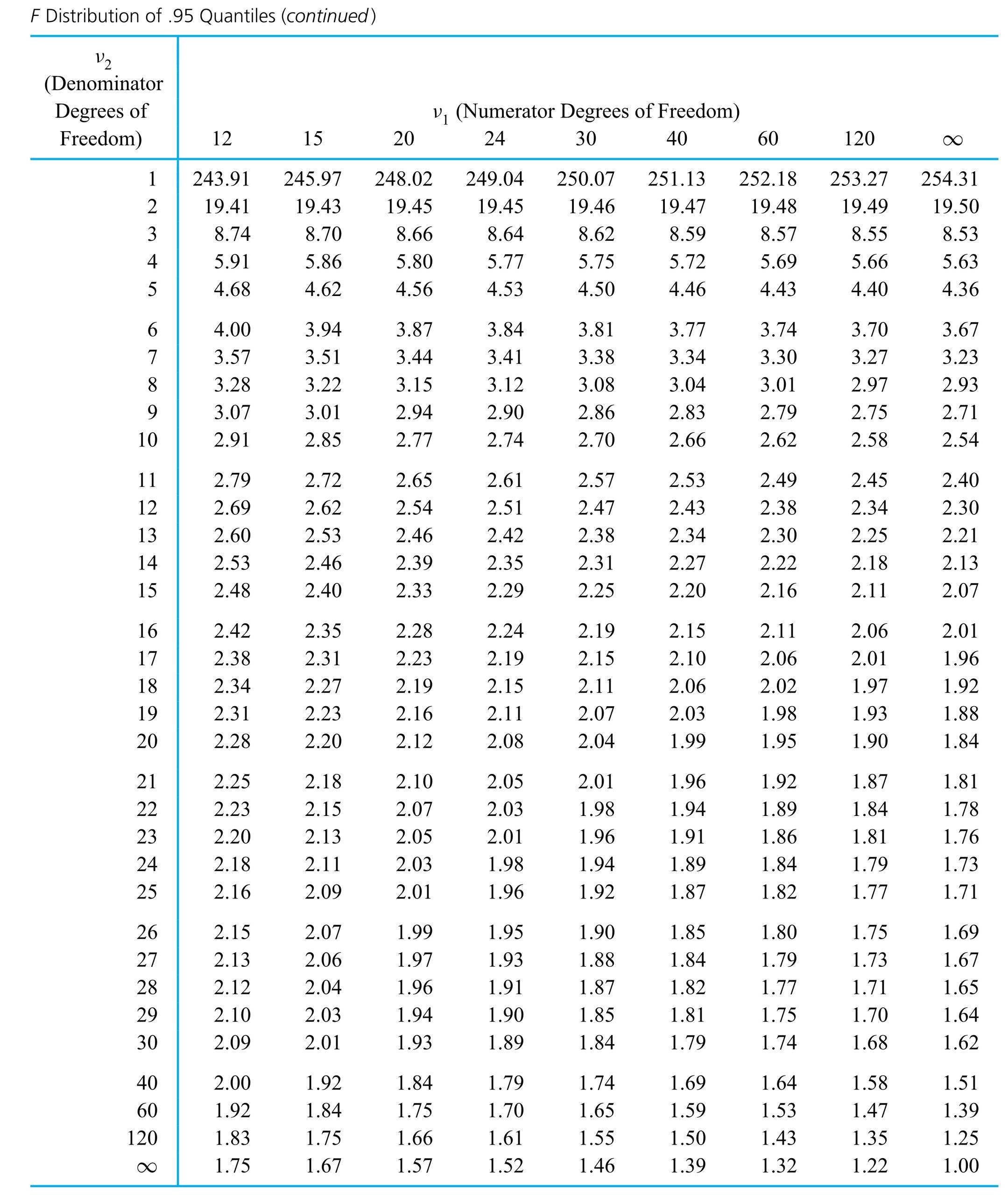
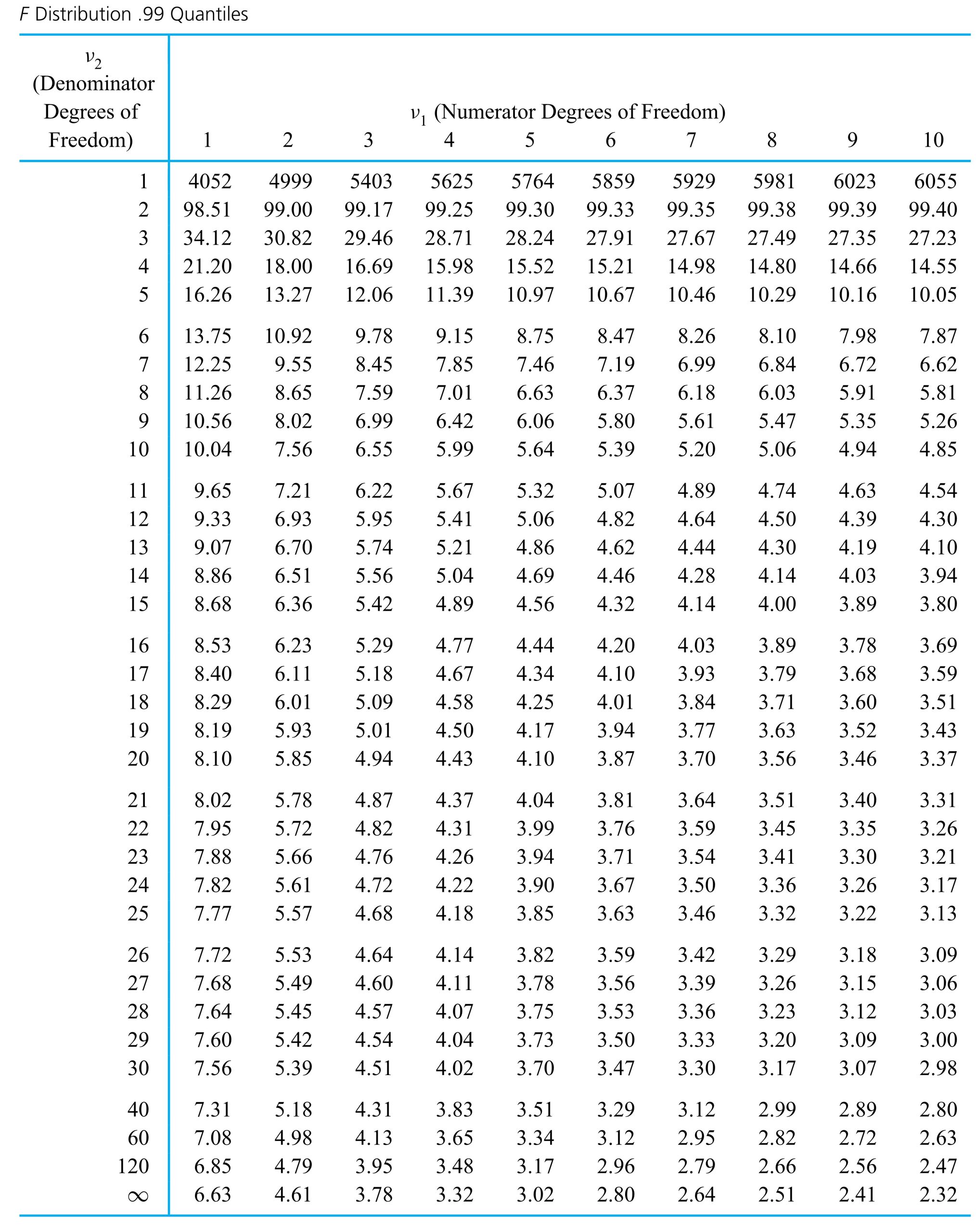
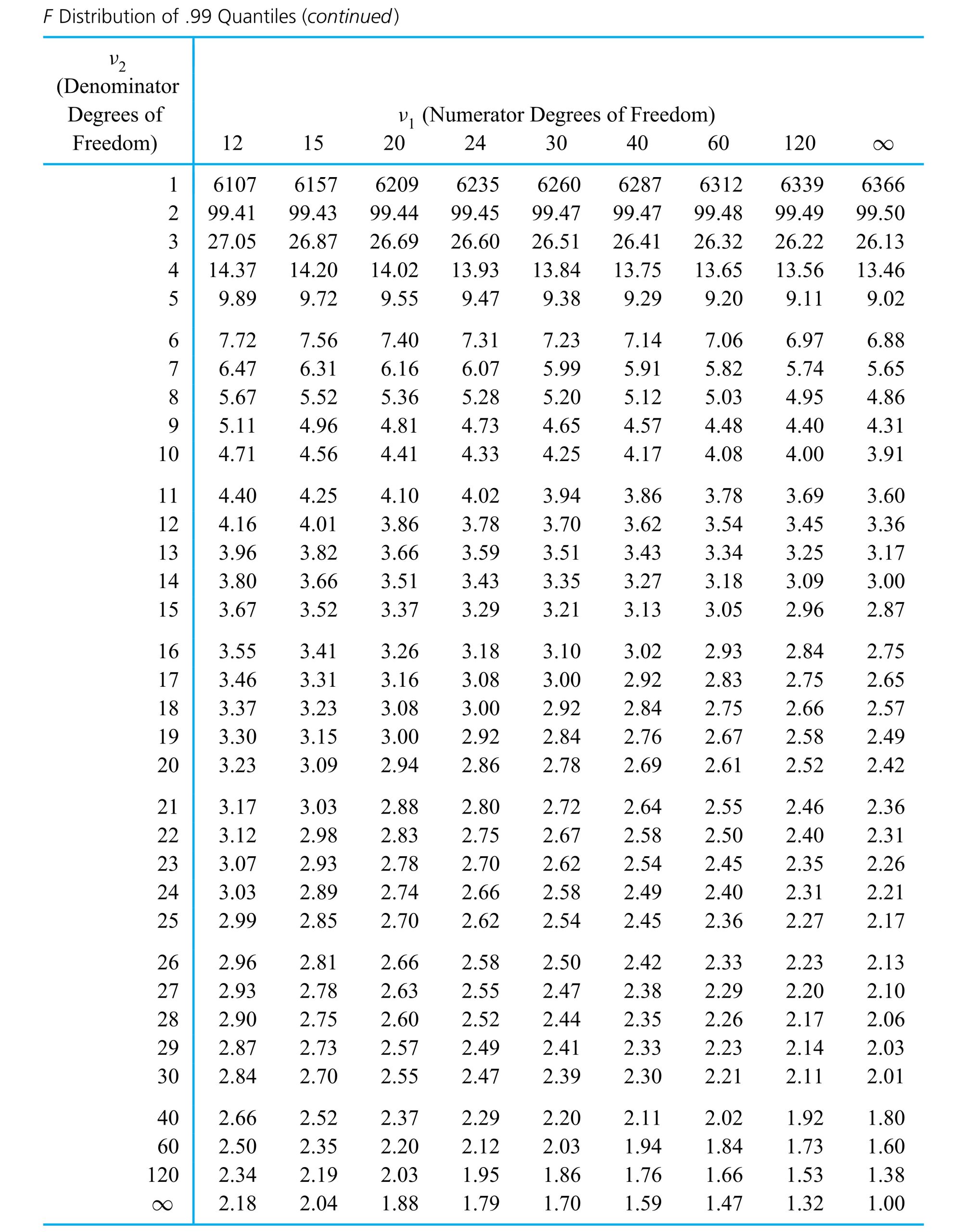
In an application, z in equation (5.1.1.6) is chosen so that the standard normal probability between −z and z corresponds to a desired confidence level. Apendix Table A1.1 (of standard normal cumulative probabilities) can be used to verify the appropriateness of the entries in Table 5.1.1.1. (This table gives values of z for use in expression (5.1.1.6) for some common confidence levels.)

Table 5.1.1.1
Dib, Smith, and Thompson studied a grinding process used in the rebuilding of automobile engines. The natural short-term variability associated with the diameters of rod journals on engine crankshafts ground using the process was on the order of σ = .7 × 10−4 in. Suppose that the rod journal grinding process can be thought of as physically stable over runs of, say, 50 journals or less. Then if 32 consecutive rod journal diameters have mean deviation from nominal of  =−.16 × 10−4 in., it is possible to apply expression (5.1.1.6) to make a confidence interval for the current process mean deviation from nominal. Consider a 95% confidence level. Consulting Table 5.1.1.1 (or otherwise, realizing that 1.96 is the p =.975 quantile of the standard normal distribution), z = 1.96 is called for in formula (5.1.1.6) (since .95 = 1 − 2(1 − .975)). Thus, a 95% confidence interval for the current process mean deviation from nominal journal diameter has endpoints
=−.16 × 10−4 in., it is possible to apply expression (5.1.1.6) to make a confidence interval for the current process mean deviation from nominal. Consider a 95% confidence level. Consulting Table 5.1.1.1 (or otherwise, realizing that 1.96 is the p =.975 quantile of the standard normal distribution), z = 1.96 is called for in formula (5.1.1.6) (since .95 = 1 − 2(1 − .975)). Thus, a 95% confidence interval for the current process mean deviation from nominal journal diameter has endpoints

that is, endpoints

An interval like this one could be of engineering importance in determining the advisability of making an adjustment to the process aim. The interval includes both positive and negative values. So although  < 0, the information in hand doesn’t provide enough precision to tell with any certainty in which direction the grinding process should be adjusted. This, coupled with the fact that potential machine adjustments are probably much coarser than the best-guess misadjustment of
< 0, the information in hand doesn’t provide enough precision to tell with any certainty in which direction the grinding process should be adjusted. This, coupled with the fact that potential machine adjustments are probably much coarser than the best-guess misadjustment of  =−.16 × 10−4 in., speaks strongly against making a change in the process aim based on the current data.
=−.16 × 10−4 in., speaks strongly against making a change in the process aim based on the current data.
A Generally Applicable Large-n Confidence Interval for 
Although expression (5.1.1.6) provides a mathematically correct confidence interval, the appearance of σ in the formula severely limits its practical usefulness. It is unusual to have to estimate a mean µ when the corresponding σ is known (and can therefore be plugged into a formula). These situations occur primarily in manufacturing situations like those of Examples 5.1.1.1 and 2. Considerable past experience can sometimes give a sensible value for σ , while physical process drifts over time can put the current value of µ in question.
Happily, modification of the line of reasoning that led to expression (5.1.1.1) produces a confidence interval formula for µ that depends only on the characteristics of a sample. The argument leading to formula (5.1.1.6) depends on the fact that for large n,  is approximately normal with mean µ and standard deviation σ/√n—i.e., that
is approximately normal with mean µ and standard deviation σ/√n—i.e., that
5.1.1.7 
is approximately standard normal. The appearance of σ in expression (5.1.1.7) is what leads to its appearance in the confidence interval formula (5.1.1.6). But a slight generalization of the central limit theorem guarantees that for large n,
5.1.1.8 
is also approximately standard normal. And the variable (5.1.1.8) doesn’t involve σ .
Beginning with the fact that (when an iid model for observations is appropriate and n is large) the variable (5.1.1.8) is approximately standard normal, the reasoning is much as before. For a positive z,
-z <  < z
< z
is equivalent to

which in turn is equivalent to

Thus, the interval with random center  and random length 2zs/√n—i.e., with random endpoints
and random length 2zs/√n—i.e., with random endpoints
EXPRESSION 5.1.1.9 Large-Sample Confidence Levels for 

can be used as an approximate confidence interval for µ. For a desired confidence, z should be chosen such that the standard normal probability between −z and z corresponds to that confidence level.
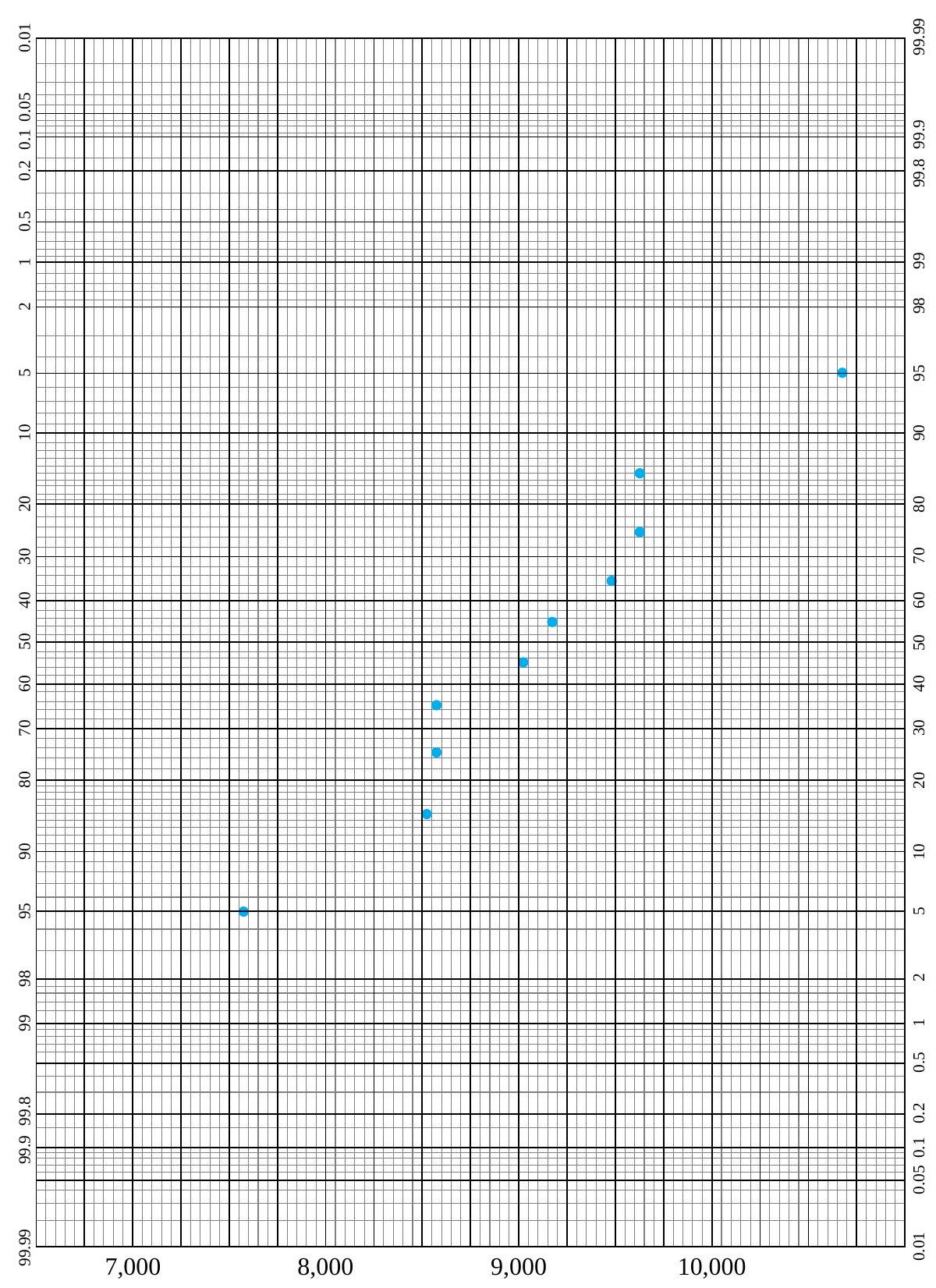
F. Willett, in the article “The Case of the Derailed Disk Drives” (Mechanical Engineering, 1988), discusses a study done to isolate the cause of “blink code A failure” in a model of Winchester hard disk drive. Included in that article are the data given in Figure 5.1.1.2. These are breakaway torques (units are inch ounces) required to loosen the drive’s interrupter flag on the stepper motor shaft for 26 disk drives returned to the manufacturer for blink code A failure. For these data,  = 11.5 in. oz and s = 5.1 in. oz.
= 11.5 in. oz and s = 5.1 in. oz.
If the disk drives that produced the data in Figure 5.1.1.2 are thought of as representing the population of drives subject to blink code A failure, it seems reasonable to use an iid model and formula (5.1.1.9) to estimate the population mean breakaway torque. Choosing to make a 90% confidence interval for µ, z = 1.645
is indicated in Table 5.1.1.1. And using formula (5.1.1.9), endpoints

(i.e., endpoints 9.9 in. oz and 13.1 in. oz) are indicated.
The interval shows that the mean breakaway torque for drives with blink code A failure was substantially below the factory’s 33.5 in. oz target value. Recognizing this turned out to be key in finding and eliminating a design flaw in the drives.
Figure 5.1.1.2 Torques required to loosen 26 interrupter flags
C: Some Comments Concerning Confidence Intervals
Formulas (5.1.1.6) and (5.1.1.9) have been used to make confidence statements of the type “µ is between a and b.” But often a statement like “µ is at least c”or“µ is no more than d ” would be of more practical value. For example, an automotive engineer might wish to state, “The mean NO emission for this engine is at most 5 ppm.” Or a civil engineer might want to make a statement like “the mean compressive strength for specimens of this type of concrete is at least 4188 psi.” That is, practical engineering problems are sometimes best addressed using one-sided confidence intervals.
Making one-sided confidence intervalsThere is no real problem in coming up with formulas for one-sided confidence intervals. If you have a workable two-sided formula, all that must be done is to
1. replace the lower limit with −∞ or the upper limit with +∞ and
2. adjust the stated confidence level appropriately upward (this usually means
dividing the “unconfidence level” by 2).
This prescription works not only with formulas (5.1.1.6) and (5.1.1.9) but also with the rest of the two-sided confidence intervals introduced in this chapter.
For the mean breakaway torque for defective disk drives, consider making a one-sided 90% confidence interval for µ of the form (−∞, #), for # an appropriate number. Put slightly differently, consider finding a 90% upper confidence bound for µ,(say,#).’
Beginning with a two-sided 80% confidence interval for µ, the lower limit canbe replaced with −∞ and a one-sided 90% confidence interval determined. Thatis, using formula (6.9), a 90% upper confidence bound for the mean breakaway torque is

Equivalently, a 90% one-sided confidence interval for µ is (−∞, 12.8).
The 12.8 in. oz figure here is less than (and closer to the sample mean than) the 13.1 in. oz upper limit from the 90% two-sided interval found earlier. In the one-sided case, −∞ is declared as a lower limit so there is no risk of producing an interval containing only numbers larger than the unknown µ. Thus an upper limit smaller than that for a corresponding two-sided interval can be used.
Interpreting a confidence interval
A second issue in the application of confidence intervals is a correct understanding of the technical meaning of the term confidence. Unfortunately, there are many possible misunderstandings. So it is important to carefully lay out what confidence
does and doesn’t mean.
Prior to selecting a sample and plugging into a formula like (5.1.1.6) or (5.1.1.9), the meaning of a confidence level is obvious. Choosing a (two-sided) 90% confidence level and thus z = 1.645 for use in formula (5.1.1.9), before the fact of sample selection and calculation, “there is about a 90% chance of winding up with an interval that brackets µ.” In symbols, this might be expressed as
![P\left[\bar{x}-1.645 \frac{s}{\sqrt{n}}<\mu<\bar{x}+1.645 \frac{s}{\sqrt{n}}\right] \approx .90 P\left[\bar{x}-1.645 \frac{s}{\sqrt{n}}<\mu<\bar{x}+1.645 \frac{s}{\sqrt{n}}\right] \approx .90](https://atu0g9ctah.execute-api.ca-central-1.amazonaws.com/latest/latex?latex=P%5Cleft%5B%5Cbar%7Bx%7D-1.645%20%5Cfrac%7Bs%7D%7B%5Csqrt%7Bn%7D%7D%3C%5Cmu%3C%5Cbar%7Bx%7D%2B1.645%20%5Cfrac%7Bs%7D%7B%5Csqrt%7Bn%7D%7D%5Cright%5D%20%5Capprox%20.90&fg=000000&font=TeX&svg=1)
But how to think about a confidence level after sample selection? This is an entirely different matter. Once numbers have been plugged into a formula like (5.1.1.6) or (5.1.1.9), the die has already been cast, and the numerical interval is either right or wrong. The practical difficulty is that while which is the case can’t be determined, it no longer makes logical sense to attach a probability to the correctness of the interval. For example, it would make no sense to look again at the two-sided interval found in Example 5.1.1.3 and try to say something like “there is a 90% probability that µ is between 9.9 in. oz and 13.1 in. oz.” µ is not a random variable. It is a fixed (although unknown) quantity that either is or is not between 9.9 and 13.1. There is no probability left in the situation to be discussed.
So what does it mean that (9.9, 13.1) is a 90% confidence interval for µ? Like it or not, the phrase “90% confidence” refers more to the method used to obtain the interval (9.9, 13.1) than to the interval itself. In coming up with the interval, methodology has been used that would produce numerical intervals bracketing µ in about 90% of repeated applications. But the effectiveness of the particular interval in this application is unknown, and it is not quantifiable in terms of a probability. A person who (in the course of a lifetime) makes many 90% confidence intervals can expect to have a “lifetime success rate” of about 90%. But the effectiveness of any particular application will typically be unknown.
A short statement summarizing this discussion as “the interpretation of confidence” will be useful.
DEFINITION 5.1.1.2 Interpretation of a Confidence Interval
To say that a numerical interval (a, b) is (for example) a 90% confidence interval for a parameter is to say that in obtaining it, one has applied methods of data collection and calculation that would produce intervals bracketing the parameter in about 90% of repeated applications. Whether or not the particular interval (a, b) brackets the parameter is unknown and not describable in terms of a probability.
The reader may feel that the statement in Definition 5.1.1.2 is a rather weak meaning for the reliability figure associated with a confidence interval. Nevertheless, the statement in Definition 5.1.1.2 is the correct interpretation and is all that can be rationally expected. And despite the fact that the correct interpretation may initially seem somewhat unappealing, confidence interval methods have proved themselves to be of great practical use.
D: Sample Sizes for estimating 
As a final consideration in this introduction to confidence intervals, note that formulas like (5.1.1.6) and (5.1.1.9) can give some crude quantitative answers to the question, “How big must n be?” Using formula (5.1.1.9), for example, if you have in mind (1) a desired confidence level, (2) a worst-case expectation for the sample standard deviation, and (3) a desired precision of estimation for µ, it is a simple matter to solve for a corresponding sample size. That is, suppose that the desired confidence level dictates the use of the value z in formula (5.1.1.9), s is some likely worst-case value for the sample standard deviation, and you want to have confidence limits (or a limit) of the form  ±
±  . Setting
. Setting

and solving for n produces the requirement

Suppose that in the disk drive problem, engineers plan to follow up the analysis of the data in Figure 5.1.1.2 with the testing of a number of new drives. This will be done after subjecting them to accelerated (high) temperature conditions, in an effort to understand the mechanism behind the creation of low breakaway torques. Further suppose that the mean breakaway torque for temperature-stressed drives is to be estimated with a two-sided 95% confidence interval and that the torque variability expected in the new temperature-stressed drives is no worse than the s = 5.1 in. oz figure obtained from the returned drives. A ±1 in. oz precision of estimation is desired. Then using the plus-or-minus part of formula (5.1.1.9) and remembering Table 5.1.1.1, the requirement is

which, when solved for n, gives

A study involving in the neighborhood of n = 100 temperature-stressed new disk drives is indicated. If this figure is impractical, the calculations at least indicate that dropping below this sample size will (unless the variability associated with the stressed new drives is less than that of the returned drives) force a reduction in either the confidence or the precision associated with the final interval.
For two reasons, the kind of calculations in the previous example give somewhat less than an ironclad answer to the question of sample size. The first is that they are only as good as the prediction of the sample standard deviation, s. If s is underpredicted, an n that is not really large enough will result. (By the same token, if one is excessively conservative and overpredicts s, an unnecessarily large sample size will result.) The second issue is that expression (5.1.1.9) remains a large-sample formula. If calculations like the preceding ones produce n smaller than, say, 25 or 30, the value should be increased enough to guarantee that formula (5.1.1.9) can be applied.



















![</span>\begin{split}\hat{y} &= b_0 + b_T x_T + b_S x_S + b_{TS} x_T x_S \\ \hat{y} &= 389.8 + 55 x_T + 134 x_S - 3.50 x_T x_S\end{split}</div> where <span class="math notranslate nohighlight">[latex]x_T = \dfrac{x_{T,\text{actual}} - \text{center}_T}{\Delta_T/2} </span>\begin{split}\hat{y} &= b_0 + b_T x_T + b_S x_S + b_{TS} x_T x_S \\ \hat{y} &= 389.8 + 55 x_T + 134 x_S - 3.50 x_T x_S\end{split}</div> where <span class="math notranslate nohighlight">[latex]x_T = \dfrac{x_{T,\text{actual}} - \text{center}_T}{\Delta_T/2}](https://atu0g9ctah.execute-api.ca-central-1.amazonaws.com/latest/latex?latex=%3C%2Fspan%3E%5Cbegin%7Bsplit%7D%5Chat%7By%7D%20%26%3D%20b_0%20%2B%20b_T%20x_T%20%2B%20b_S%20x_S%20%2B%20b_%7BTS%7D%20x_T%20x_S%20%5C%5C%20%20%5Chat%7By%7D%20%26%3D%20389.8%20%2B%2055%20x_T%20%2B%20134%20x_S%20-%203.50%20x_T%20x_S%5Cend%7Bsplit%7D%3C%2Fdiv%3E%20%20where%20%3Cspan%20class%3D%22math%20notranslate%20nohighlight%22%3E%5Blatex%5Dx_T%20%3D%20%5Cdfrac%7Bx_%7BT%2C%5Ctext%7Bactual%7D%7D%20-%20%5Ctext%7Bcenter%7D_T%7D%7B%5CDelta_T%2F2%7D&fg=000000&font=TeX&svg=1)






































 =
= 
 in free fall an object will have velocity
in free fall an object will have velocity =
= 

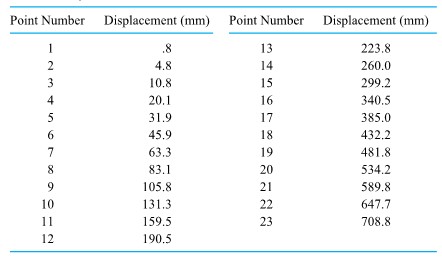
 of a second. Table 1.1.7.1 gives measurements of such positions. (Dr. Frank Peterson of the ISU Physics and Astronomy Department supplied the tape.) Plotting the bob positions in the table at equally spaced intervals produces the approximately quadratic plot shown in Figure 1.1.7.2. Picking a parabola to fit the plotted points involves identifying an appropriate value for
of a second. Table 1.1.7.1 gives measurements of such positions. (Dr. Frank Peterson of the ISU Physics and Astronomy Department supplied the tape.) Plotting the bob positions in the table at equally spaced intervals produces the approximately quadratic plot shown in Figure 1.1.7.2. Picking a parabola to fit the plotted points involves identifying an appropriate value for  /
/ , not far from the commonly quoted value of 9.8
, not far from the commonly quoted value of 9.8 

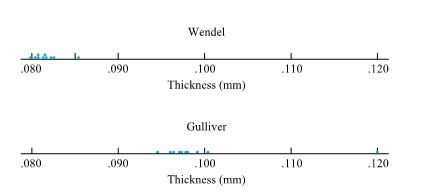
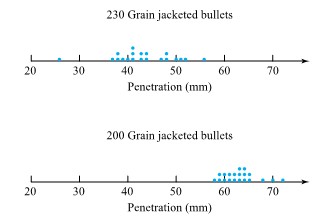
 from the target surface to the back of the bullets) for two bullet types. Figure 2.2.2.2 presents a corresponding pair of dot diagrams.
from the target surface to the back of the bullets) for two bullet types. Figure 2.2.2.2 presents a corresponding pair of dot diagrams.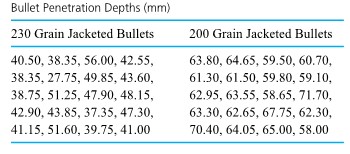

 ” and ”
” and ”  ” leaf positions for each possible leading digit, instead of only a single ”
” leaf positions for each possible leading digit, instead of only a single ”  ” leaf for each leading digit.
” leaf for each leading digit.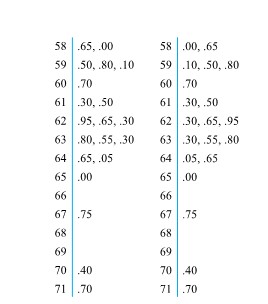



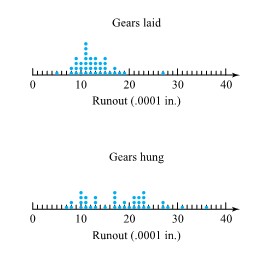
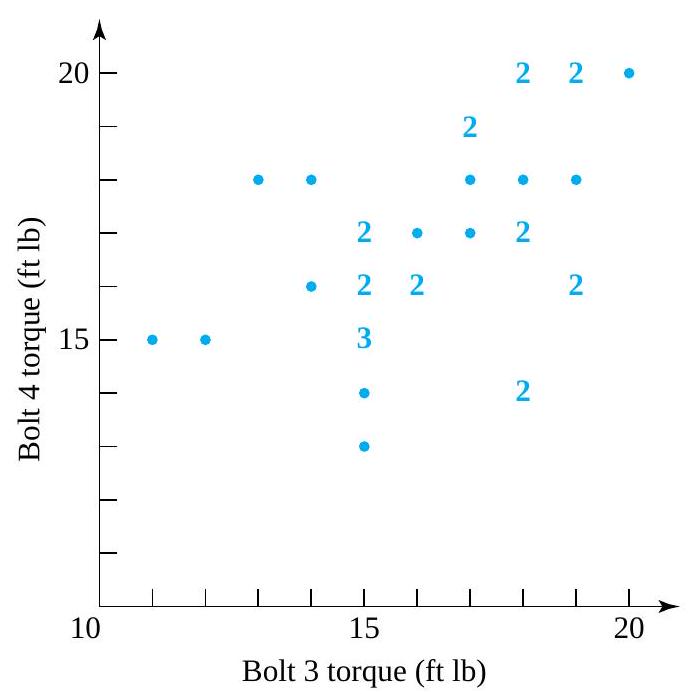
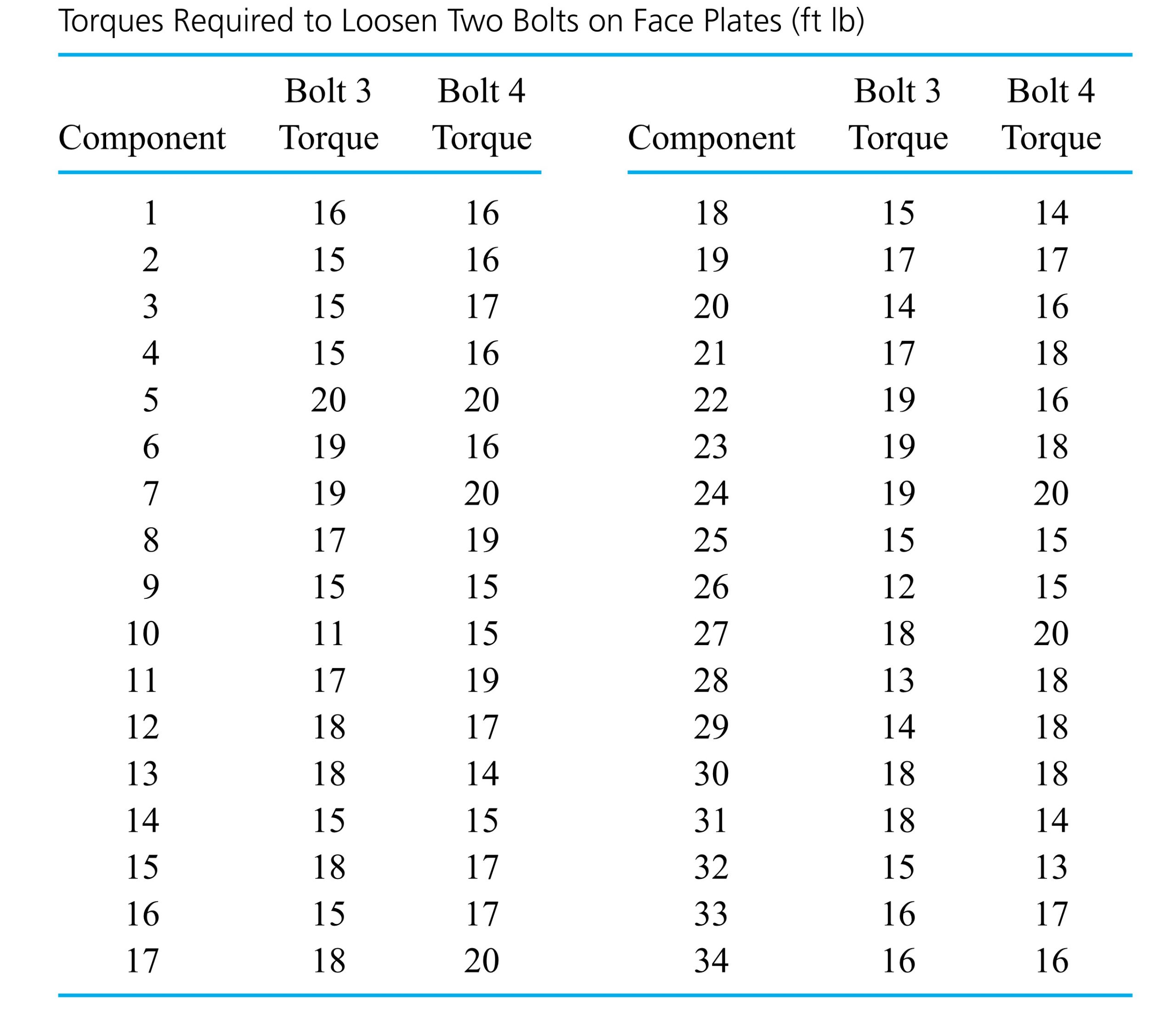
 required for bolts number 3 and 4), respectively, on 34 different components. Figure 2.1.4.1 is a scatterplot of the bivariate data from Table 2.1.4.1. In this figure, where several points must be plotted at a single location, the number of points occupying the location has been plotted instead of a single dot.
required for bolts number 3 and 4), respectively, on 34 different components. Figure 2.1.4.1 is a scatterplot of the bivariate data from Table 2.1.4.1. In this figure, where several points must be plotted at a single location, the number of points occupying the location has been plotted instead of a single dot.

 of those taking the test had worse scores, and roughly
of those taking the test had worse scores, and roughly  had better scores. This concept is also useful in the description of engineering data. However, because it is often more convenient to work in terms of fractions between 0 and 1 rather than in percentages between 0 and 100, slightly different terminology will be used here: “Quantiles,” rather than percentiles, will be discussed. After the quantiles of a data set are carefully defined, they are used to create a number of useful tools of descriptive statistics: quantile plots, boxplots,
had better scores. This concept is also useful in the description of engineering data. However, because it is often more convenient to work in terms of fractions between 0 and 1 rather than in percentages between 0 and 100, slightly different terminology will be used here: “Quantiles,” rather than percentiles, will be discussed. After the quantiles of a data set are carefully defined, they are used to create a number of useful tools of descriptive statistics: quantile plots, boxplots,  plots, and normal plots (a type of theoretical
plots, and normal plots (a type of theoretical  between 0 and 1 , the
between 0 and 1 , the  of the distribution lies to the right. However, because of the discreteness of finite data sets, it is necessary to state exactly what will be meant by the terminology. Definition 1 gives the precise convention that will be used in this text.
of the distribution lies to the right. However, because of the discreteness of finite data sets, it is necessary to state exactly what will be meant by the terminology. Definition 1 gives the precise convention that will be used in this text. values that when ordered are
values that when ordered are  ,
, for a positive integer
for a positive integer  , the
, the 
 quantile.)
quantile.) and
and  that is not of the form
that is not of the form  , the
, the  with corresponding
with corresponding  will be used to denote the
will be used to denote the  and
and  . To find
. To find  for
for 
 th ordered data point.”
th ordered data point.” , one can easily find the
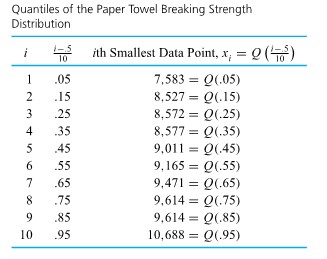
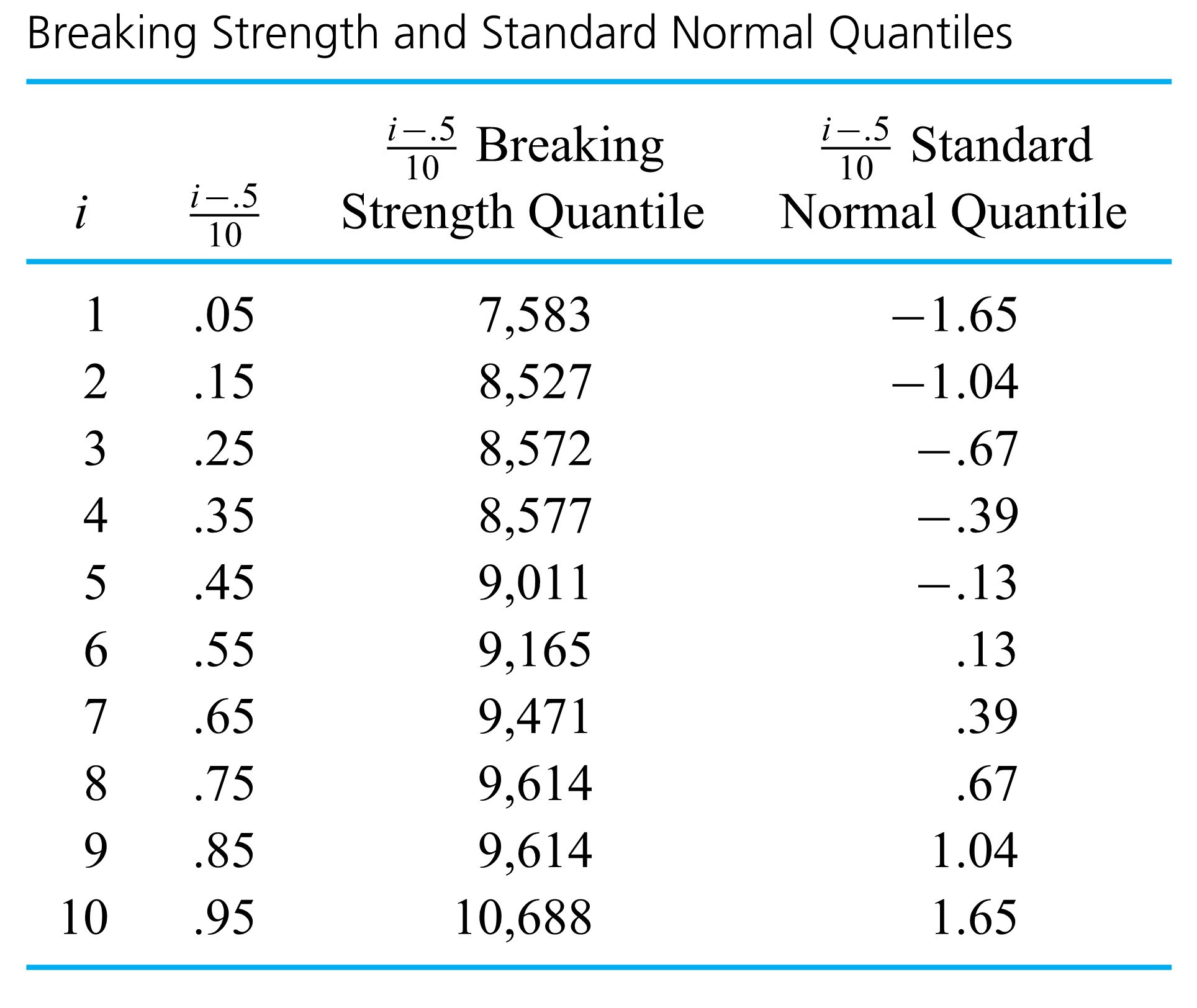
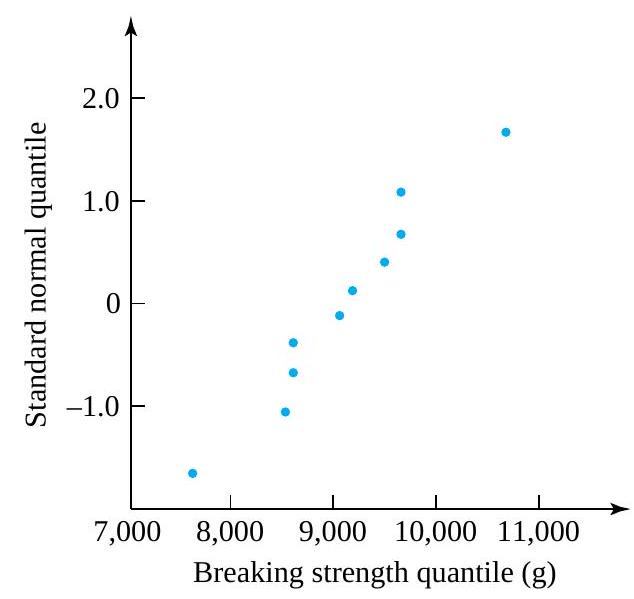
, one can easily find the  , and .95 quantiles of the breaking strength distribution, as shown in Table 31.5.2.
, and .95 quantiles of the breaking strength distribution, as shown in Table 31.5.2.
 data points, each one accounts for
data points, each one accounts for  of the data set. Applying convention (1) in Definition 3.1.5.1 to find (for example) the .35 quantile, the smallest 3 data points and half of the fourth smallest are counted as lying to (continued) the left of the desired number, and the largest 6 data points and half of the seventh largest are counted as lying to the right. Thus, the fourth smallest data point must be the .35 quantile, as is shown in Table 2.1.5.2.
of the data set. Applying convention (1) in Definition 3.1.5.1 to find (for example) the .35 quantile, the smallest 3 data points and half of the fourth smallest are counted as lying to (continued) the left of the desired number, and the largest 6 data points and half of the seventh largest are counted as lying to the right. Thus, the fourth smallest data point must be the .35 quantile, as is shown in Table 2.1.5.2. of the way from .45 to .55 , linear interpolation gives:
of the way from .45 to .55 , linear interpolation gives:
 of the way from .85 to .95 , linear interpolation gives:
of the way from .85 to .95 , linear interpolation gives:
 is called the median of a distribution.
is called the median of a distribution. and
and  are called the first (or lower) quartile and third (or upper) quartile of a distribution, respectively.
are called the first (or lower) quartile and third (or upper) quartile of a distribution, respectively. previously computed, for the (continued) breaking strength distribution
previously computed, for the (continued) breaking strength distribution
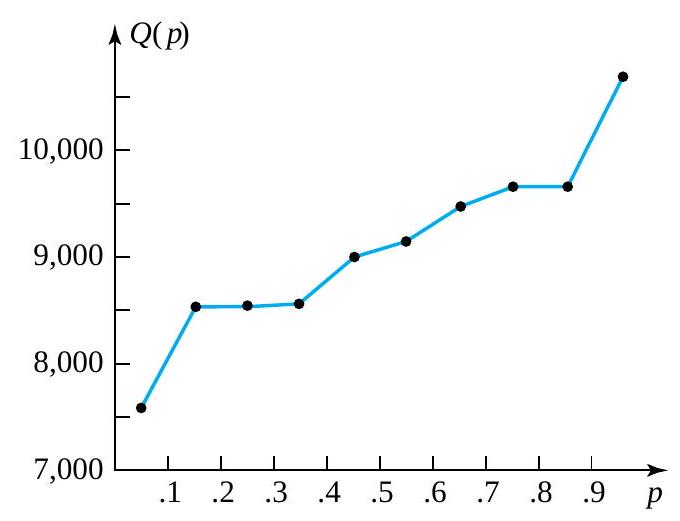
 and then connecting consecutive plotted points with straight-line segments.
and then connecting consecutive plotted points with straight-line segments.

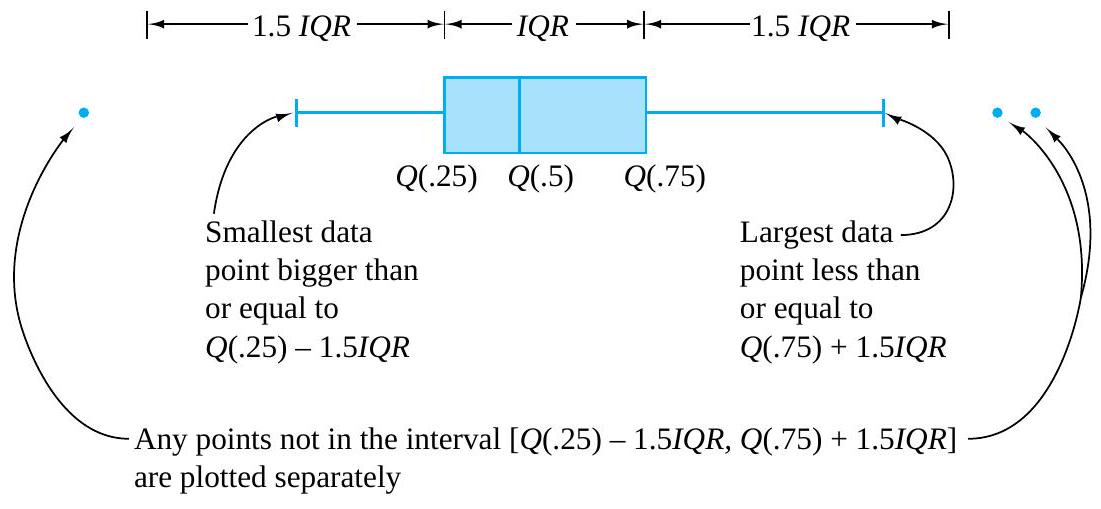
 and the largest data point within 1.5IQR of
and the largest data point within 1.5IQR of ![[Q(.25)-1.5 I Q R, Q(.75)+1.5 I Q R] [Q(.25)-1.5 I Q R, Q(.75)+1.5 I Q R]](https://atu0g9ctah.execute-api.ca-central-1.amazonaws.com/latest/latex?latex=%5BQ%28.25%29-1.5%20I%20Q%20R%2C%20Q%28.75%29%2B1.5%20I%20Q%20R%5D&fg=000000&font=TeX&svg=1) . Any that are not then get plotted individually and are thereby identified as outlying or unusual.
. Any that are not then get plotted individually and are thereby identified as outlying or unusual.




 to
to  , the boxplot is as shown in Figure 2.1.6.2.
, the boxplot is as shown in Figure 2.1.6.2.
 of the distribution. Some elements of distributional shape are indicated by the symmetry (or lack thereof) of the box and of the whiskers. And a gap between the end of a whisker and a separately plotted point serves as a reminder that no data values fall in that interval.
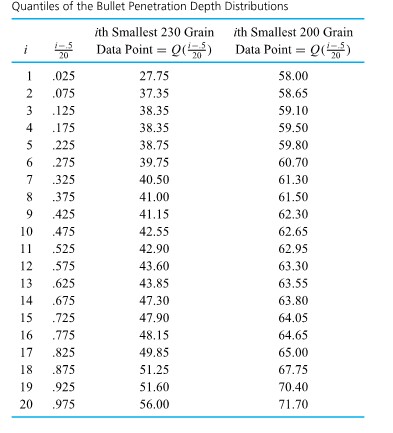
of the distribution. Some elements of distributional shape are indicated by the symmetry (or lack thereof) of the box and of the whiskers. And a gap between the end of a whisker and a separately plotted point serves as a reminder that no data values fall in that interval. quantiles for the two distributions of bullet penetration depth introduced in the previous section. For the 230 grain bullet penetration depths, interpolation yields
quantiles for the two distributions of bullet penetration depth introduced in the previous section. For the 230 grain bullet penetration depths, interpolation yields



 plot.
plot. th smallest value in data set 1
th smallest value in data set 1
 and
and  stand for the quantile functions of the two respective data sets, it is clear from display (2.1.7.1) that
stand for the quantile functions of the two respective data sets, it is clear from display (2.1.7.1) that


 ) should be exactly linear. Figure 3.16 illustrates this-in fact Figure 3.16 is a
) should be exactly linear. Figure 3.16 illustrates this-in fact Figure 3.16 is a  for appropriate values of
for appropriate values of  . When two data sets of unequal sizes are involved, the values of
. When two data sets of unequal sizes are involved, the values of  and
and  (for the 230 grain data) is out of proportion to the gap between 63.55 and
(for the 230 grain data) is out of proportion to the gap between 63.55 and  (for the 200 grain data). This hints that there was some kind of basic physical difference in the mechanisms that produced the smaller and larger 230 grain penetration depths. Once this kind of indication is discovered, it is a task for ballistics experts or materials people to explain the phenomenon.
(for the 200 grain data). This hints that there was some kind of basic physical difference in the mechanisms that produced the smaller and larger 230 grain penetration depths. Once this kind of indication is discovered, it is a task for ballistics experts or materials people to explain the phenomenon. , there is also a drastic difference in the shapes of the extreme lower ends of the two distributions. In order to move that point back on line with the rest of the plotted points, it would need to be moved to the right or down (i.e., increase the smallest 230 grain observation or decrease the smallest 200 grain observation). That is, relative to the 200 grain distribution, the 230 grain distribution is long-tailed to the low side. (Or to put it differently, relative to the 230 grain distribution, the 200 grain distribution is short-tailed to the low side.) Note that the difference in shapes was already evident in the boxplot in Figure previously. Again, it would remain for a specialist to explain this difference in distributional shapes.
, there is also a drastic difference in the shapes of the extreme lower ends of the two distributions. In order to move that point back on line with the rest of the plotted points, it would need to be moved to the right or down (i.e., increase the smallest 230 grain observation or decrease the smallest 200 grain observation). That is, relative to the 200 grain distribution, the 230 grain distribution is long-tailed to the low side. (Or to put it differently, relative to the 230 grain distribution, the 200 grain distribution is short-tailed to the low side.) Note that the difference in shapes was already evident in the boxplot in Figure previously. Again, it would remain for a specialist to explain this difference in distributional shapes.

 , locate the entry in the row labelled by the first digit after the decimal place and in the column labelled by the second digit after the decimal place. (For example,
, locate the entry in the row labelled by the first digit after the decimal place and in the column labelled by the second digit after the decimal place. (For example,  .) A simple numerical approximation to the values given in Table 3.10 adequate for most plotting purposes is
.) A simple numerical approximation to the values given in Table 3.10 adequate for most plotting purposes is
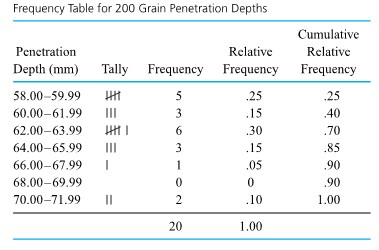
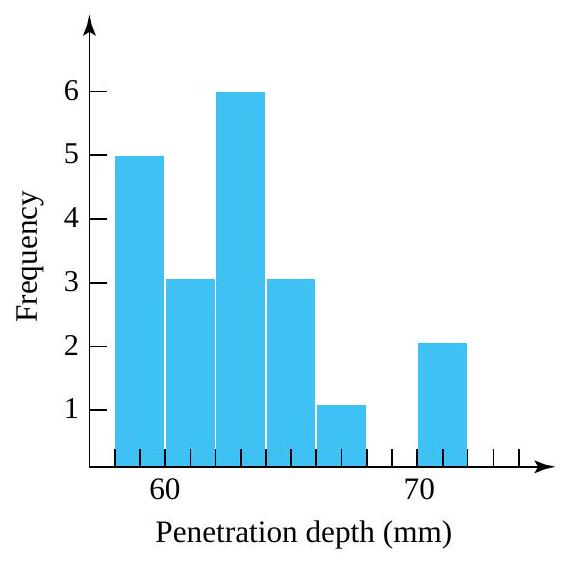
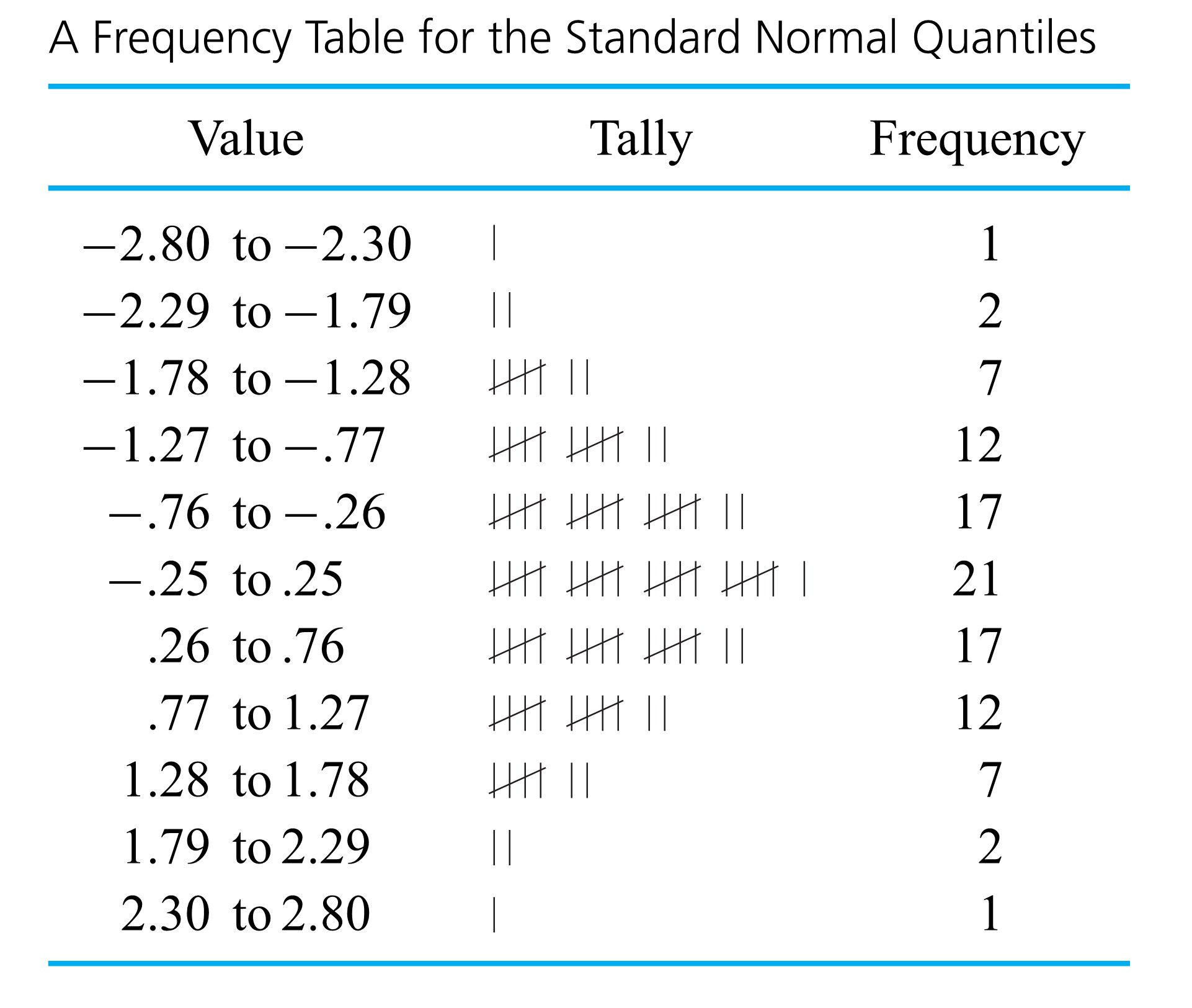
 . A possible frequency table for those 99 data points is given as Table 2.1.7.3. The tally column in Table 2.1.7.3 shows clearly the bell shape.
. A possible frequency table for those 99 data points is given as Table 2.1.7.3. The tally column in Table 2.1.7.3 shows clearly the bell shape.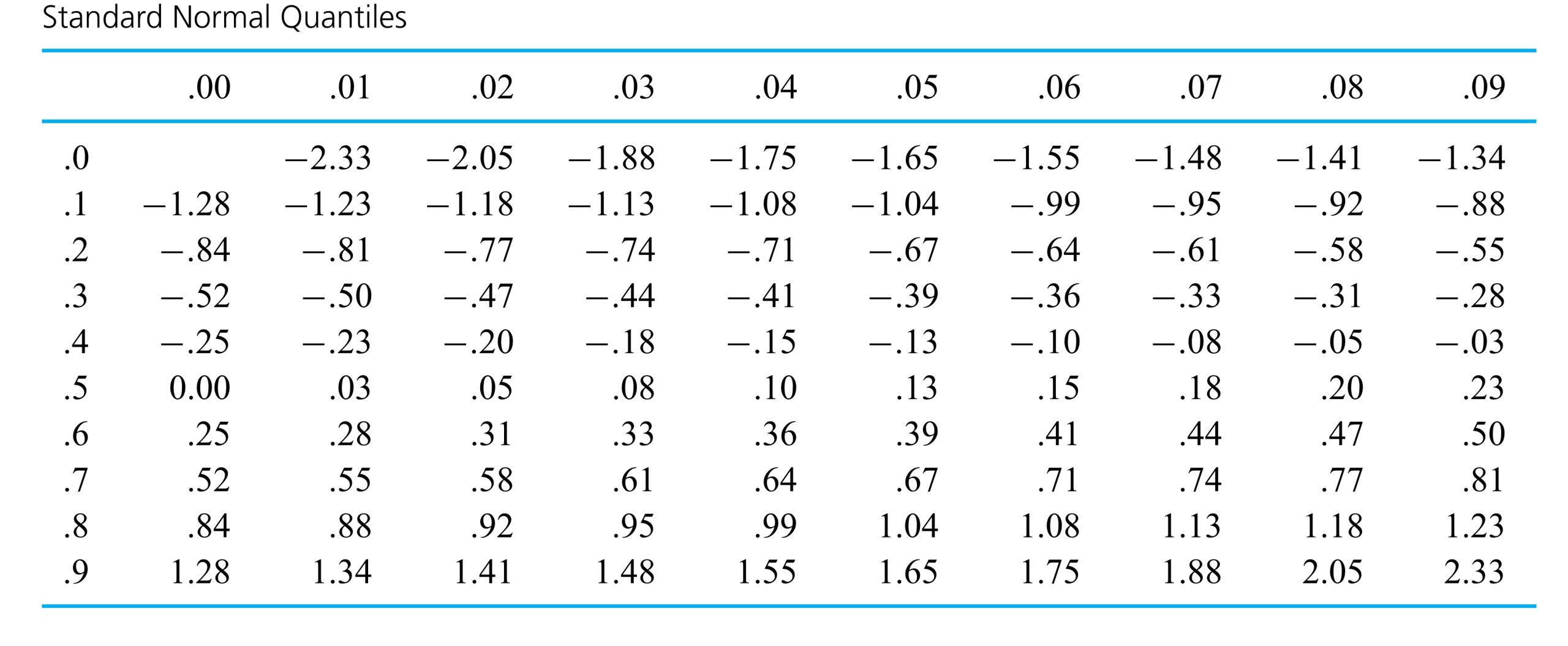
![Q-Q[l/atex] plotting here makes it possible to emphasize the relationship between probability plotting and (empirical) [latex]Q-Q Q-Q[l/atex] plotting here makes it possible to emphasize the relationship between probability plotting and (empirical) [latex]Q-Q](https://atu0g9ctah.execute-api.ca-central-1.amazonaws.com/latest/latex?latex=Q-Q%5Bl%2Fatex%5D%20plotting%20here%20makes%20it%20possible%20to%20emphasize%20the%20relationship%20between%20probability%20plotting%20and%20%28empirical%29%20%5Blatex%5DQ-Q&fg=000000&font=TeX&svg=1) plotting.
plotting.
 and/or the value 2 is replaced by
and/or the value 2 is replaced by  .
. , is
, is
 .
.



 is
is
 .” Since the range depends only on the values of the smallest and largest points in a data set, it is necessarily highly sensitive to extreme (or outlying) values. Because it is easily calculated, it has enjoyed long-standing popularity in industrial settings, particularly as a tool in statistical quality control.
.” Since the range depends only on the values of the smallest and largest points in a data set, it is necessarily highly sensitive to extreme (or outlying) values. Because it is easily calculated, it has enjoyed long-standing popularity in industrial settings, particularly as a tool in statistical quality control. is
is
 , is the nonnegative square root of the sample variance.
, is the nonnegative square root of the sample variance. for
for  is an average squared distance of the data points from the central value
is an average squared distance of the data points from the central value 








 and
and  to stand for the population mean and to write:
to stand for the population mean and to write:
 is used in place of
is used in place of  to stand for the population variance and to define:
to stand for the population variance and to define:
 is then called the population standard deviation,
is then called the population standard deviation,  .
.
 different
different 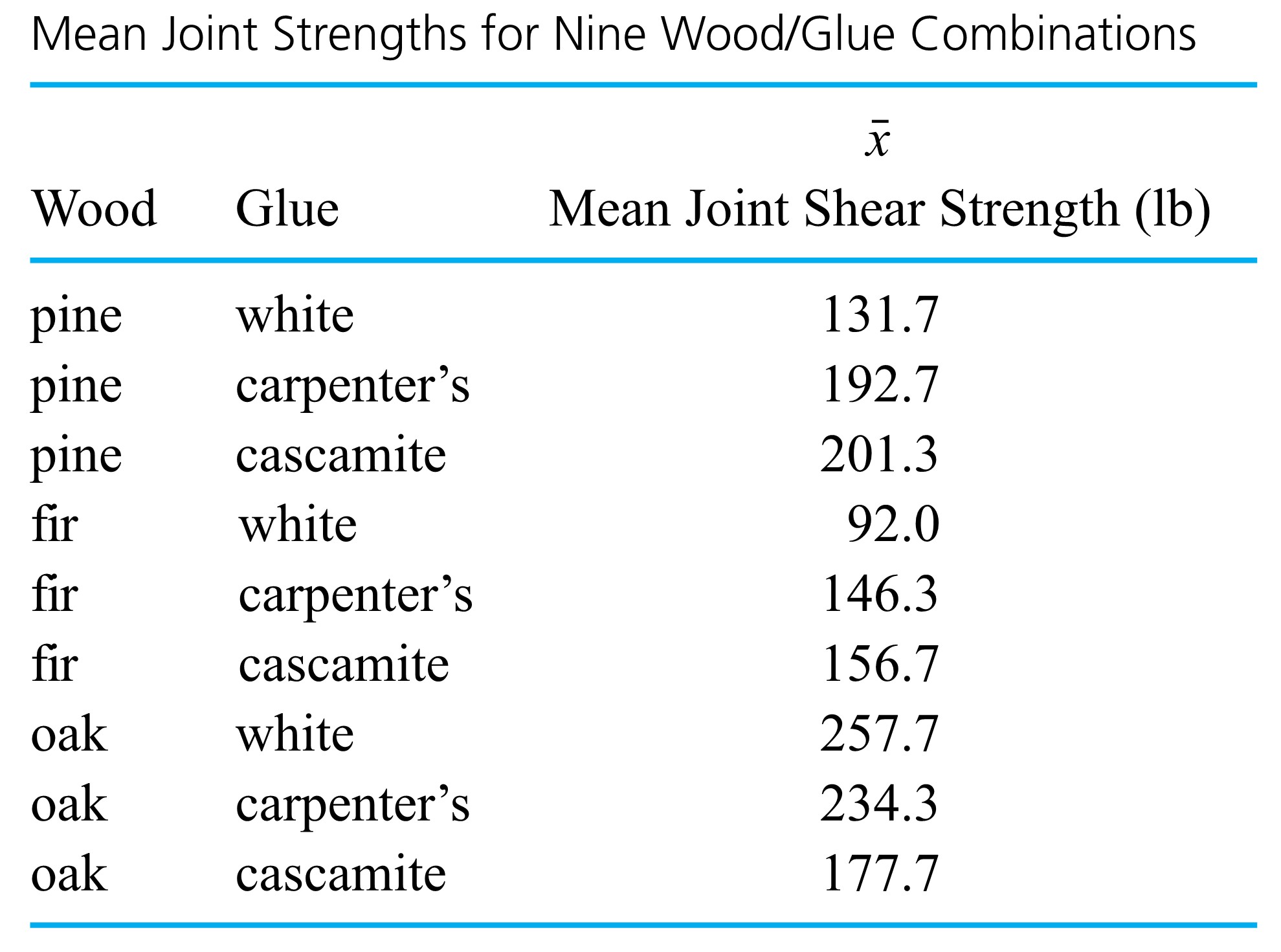
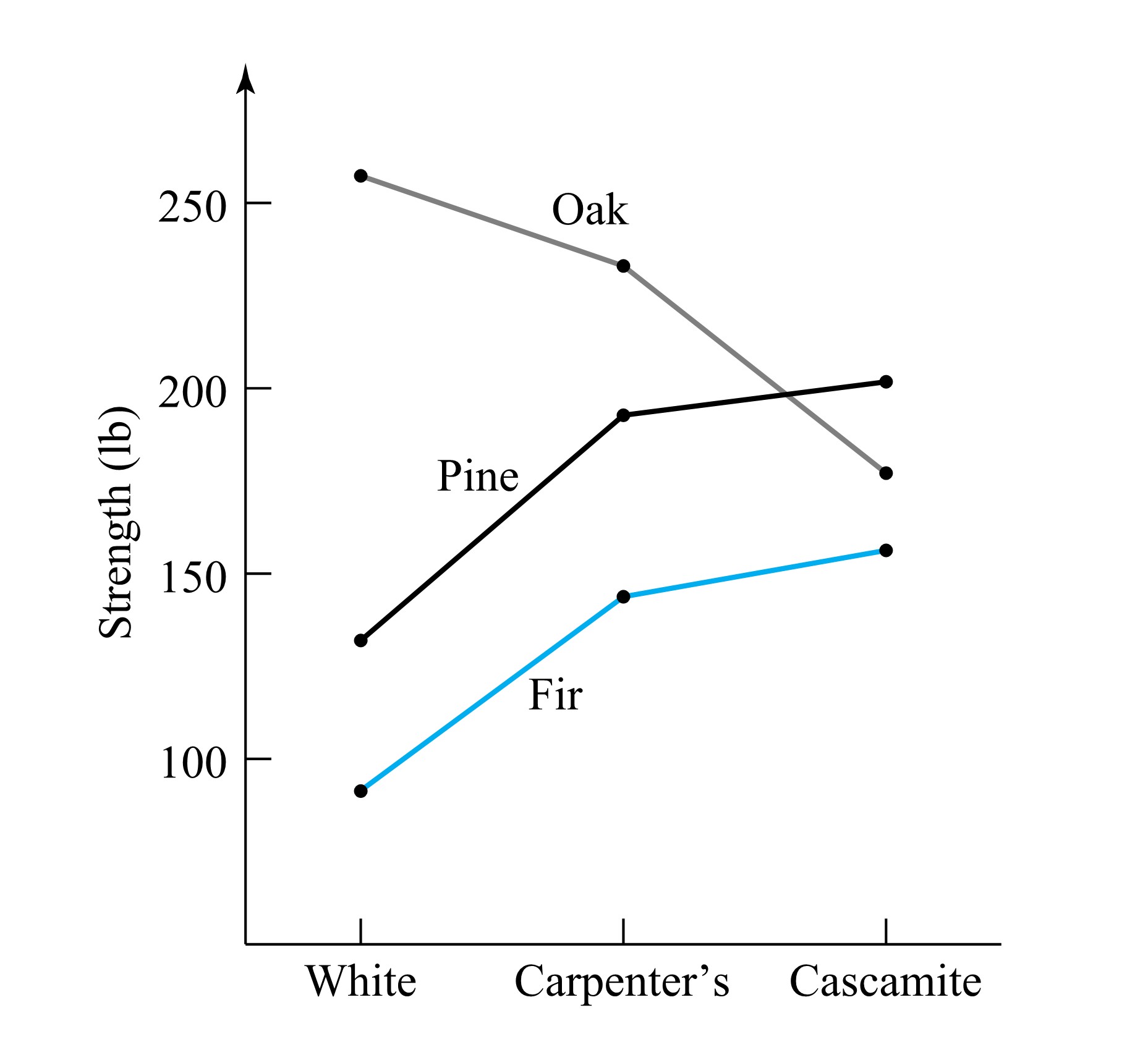
 or
or  that need to be compared. Bar charts and simple bivariate plots can be a great aid in summarizing these results.
that need to be compared. Bar charts and simple bivariate plots can be a great aid in summarizing these results.![30 \times 100=3,000[latex] connectors were inspected over this period,</div> <div> <div style="text-align: center">[latex]\begin{aligned}& \hat{p}_{\mathrm{A}}=3 / 3000=.0010 \\& \hat{p}_{\mathrm{B}}=0 / 3000=.0000 \\& \hat{p}_{\mathrm{C}}=11 / 3000=.0037 \\& \hat{p}_{\mathrm{D}}=1 / 3000=.0003\end{aligned} 30 \times 100=3,000[latex] connectors were inspected over this period,</div> <div> <div style="text-align: center">[latex]\begin{aligned}& \hat{p}_{\mathrm{A}}=3 / 3000=.0010 \\& \hat{p}_{\mathrm{B}}=0 / 3000=.0000 \\& \hat{p}_{\mathrm{C}}=11 / 3000=.0037 \\& \hat{p}_{\mathrm{D}}=1 / 3000=.0003\end{aligned}](https://atu0g9ctah.execute-api.ca-central-1.amazonaws.com/latest/latex?latex=30%20%5Ctimes%20100%3D3%2C000%5Blatex%5D%20connectors%20were%20inspected%20over%20this%20period%2C%3C%2Fdiv%3E%20%20%3Cdiv%3E%20%20%3Cdiv%20style%3D%22text-align%3A%20center%22%3E%5Blatex%5D%5Cbegin%7Baligned%7D%26%20%5Chat%7Bp%7D_%7B%5Cmathrm%7BA%7D%7D%3D3%20%2F%203000%3D.0010%20%5C%5C%26%20%5Chat%7Bp%7D_%7B%5Cmathrm%7BB%7D%7D%3D0%20%2F%203000%3D.0000%20%5C%5C%26%20%5Chat%7Bp%7D_%7B%5Cmathrm%7BC%7D%7D%3D11%20%2F%203000%3D.0037%20%5C%5C%26%20%5Chat%7Bp%7D_%7B%5Cmathrm%7BD%7D%7D%3D1%20%2F%203000%3D.0003%5Cend%7Baligned%7D&fg=000000&font=TeX&svg=1)
 , because categories A through E represent a set of nonoverlapping and exhaustive classifications into which an individual connector must fall, so that the
, because categories A through E represent a set of nonoverlapping and exhaustive classifications into which an individual connector must fall, so that the 
 , having moderately serious defects but no serious or very serious defects. This bar chart is a presentation of the behavior of a single categorical variable.
, having moderately serious defects but no serious or very serious defects. This bar chart is a presentation of the behavior of a single categorical variable.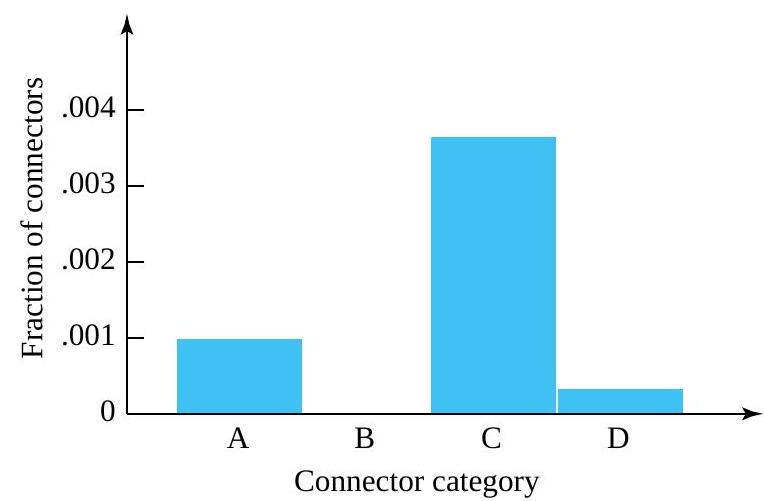

 , so
, so  for the fraction of tools without type 1 leaks. The
for the fraction of tools without type 1 leaks. The 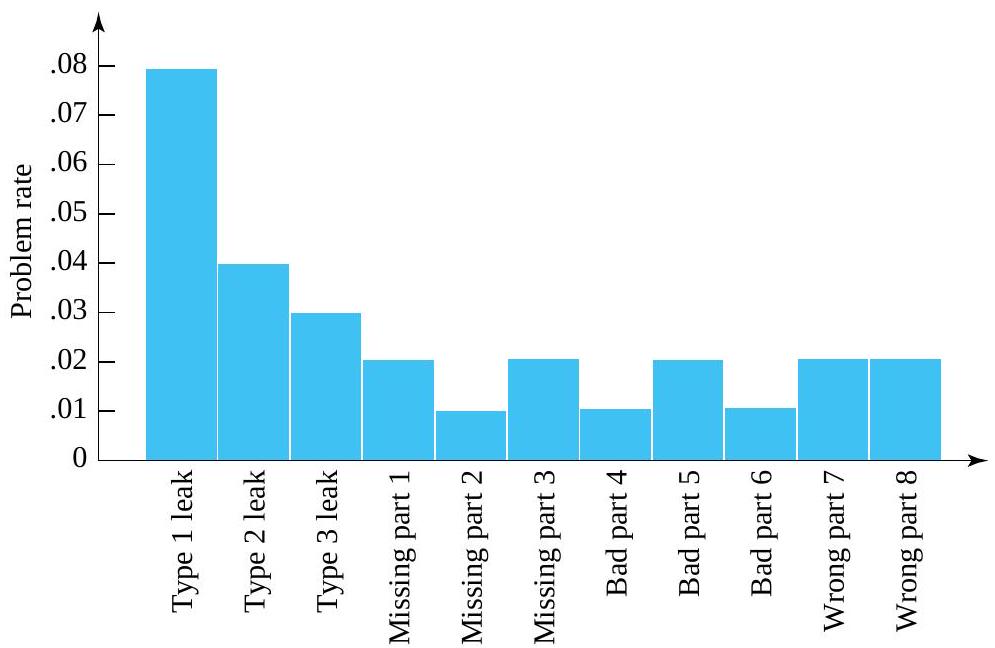
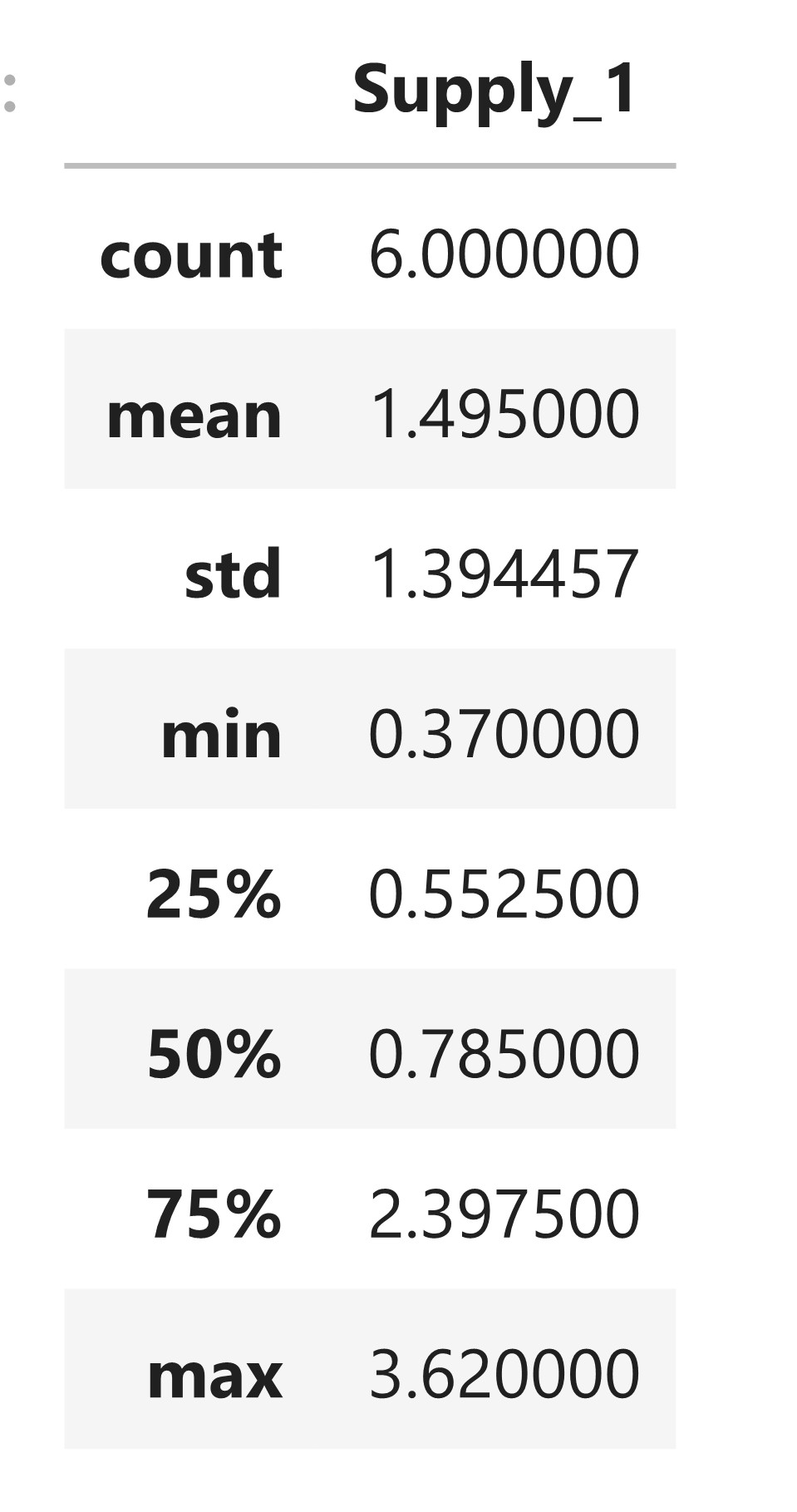
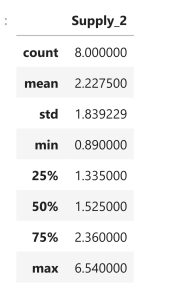
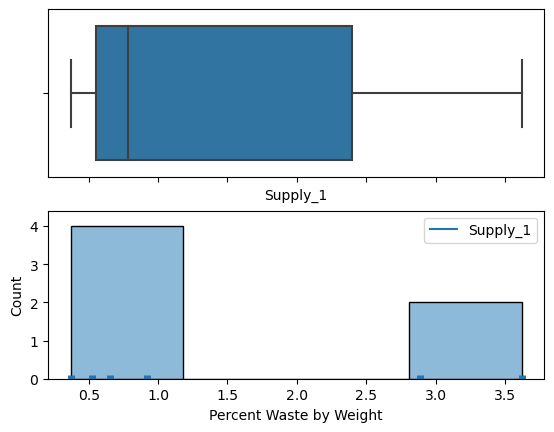

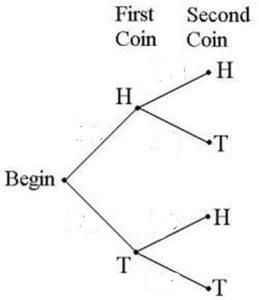
 where H = heads and T = tails are the outcomes. The sample space for flipping two fair coins once is shown: S = {(HH),(HT),(TH),(TT)}. We will also use capital letters to denote an event, like A and B. For example, we can define event A as realizing tails on the first coin and event B= tails on the second coin. This would be shown as
where H = heads and T = tails are the outcomes. The sample space for flipping two fair coins once is shown: S = {(HH),(HT),(TH),(TT)}. We will also use capital letters to denote an event, like A and B. For example, we can define event A as realizing tails on the first coin and event B= tails on the second coin. This would be shown as  and
and  . Using diagrams is helpful in representing the operations of multiple events together.
. Using diagrams is helpful in representing the operations of multiple events together. is in neither
is in neither  nor
nor  . The Venn diagram is as follows:
. The Venn diagram is as follows: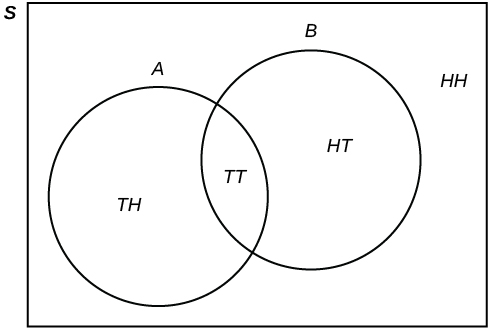
 . The marginal events are those shown on the margins of the table, and are those that occur for a single event with no regard for the other events in the table. For our example, we have marginal event A and the associated joint events,
. The marginal events are those shown on the margins of the table, and are those that occur for a single event with no regard for the other events in the table. For our example, we have marginal event A and the associated joint events, 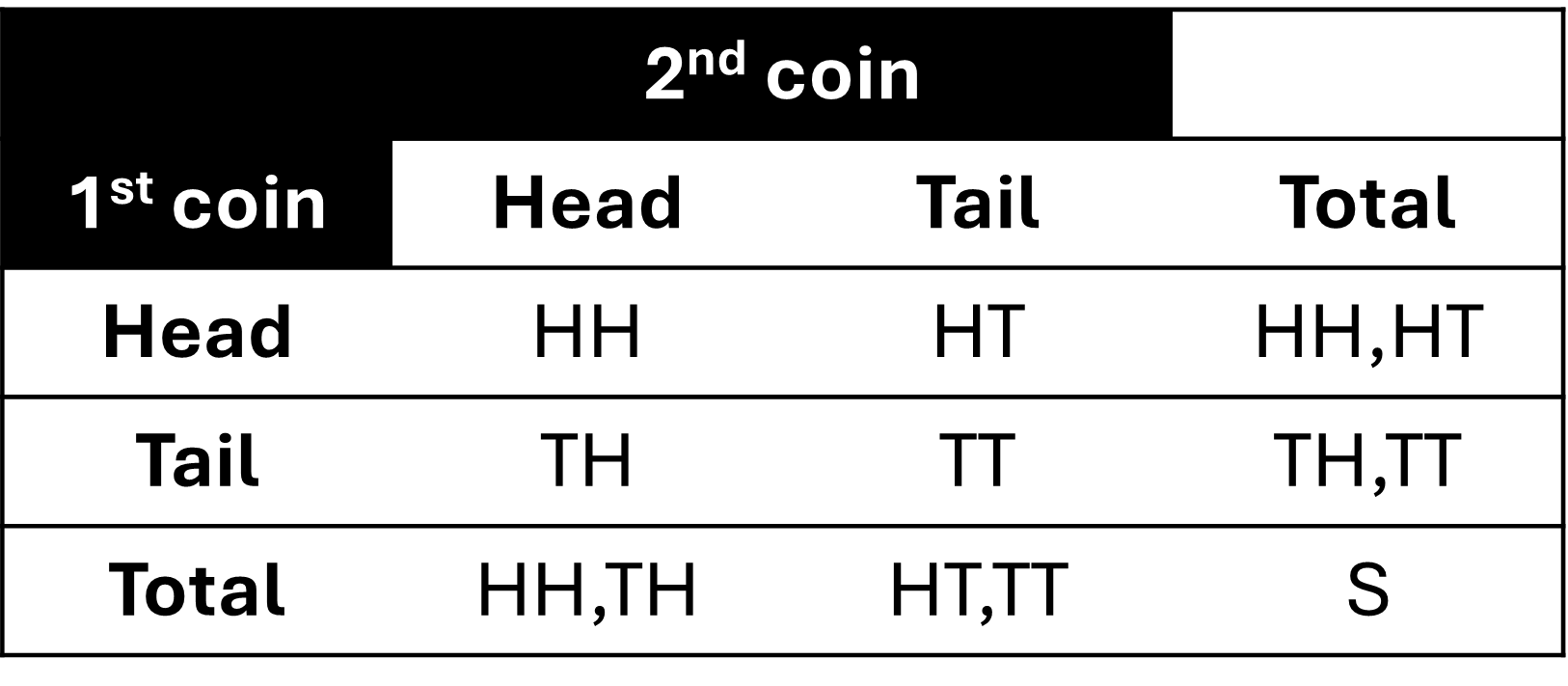
 .
. .
. .
. .
. is the set of outcomes that are in both
is the set of outcomes that are in both  is the set of outcomes that are in either
is the set of outcomes that are in either  . Therefore
. Therefore  is the set of outcomes that are not in
is the set of outcomes that are not in  , with m being the number of outcomes in the the event A occurs and n being the total number of outcomes of the experiment. A claim of the frequentist approach is that, as the number of trials increases, the change in the relative frequency will diminish. Hence, one can view a probability as the limiting value of the corresponding relative frequencies. You can realize the relative frequency by either running real experiments and finding an empirical or estimated probability or by recognizing the theoretical model for the experiment and adopting a theoretical probability based on events from the sample space.
, with m being the number of outcomes in the the event A occurs and n being the total number of outcomes of the experiment. A claim of the frequentist approach is that, as the number of trials increases, the change in the relative frequency will diminish. Hence, one can view a probability as the limiting value of the corresponding relative frequencies. You can realize the relative frequency by either running real experiments and finding an empirical or estimated probability or by recognizing the theoretical model for the experiment and adopting a theoretical probability based on events from the sample space.
 = 0.5.
= 0.5.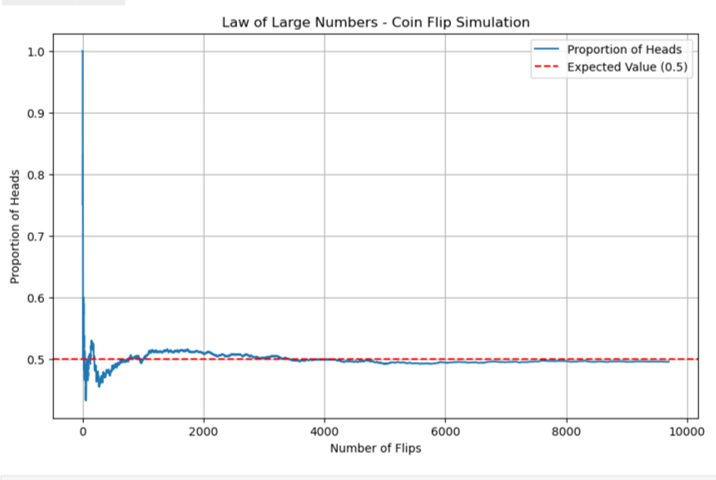
 , is assigned a number between zero and one, inclusive, and describes the proportion of time we expect the event to occur over the long-term. P(A) = 0 means the event A can never happen. P(A) = 1 means the event A always happens. P(A) = 0.5 means the event A is equally likely to occur or not to occur. For example, if you flip one fair coin repeatedly (from 20 to 2,000 to 20,000 times) the relative frequency of heads approaches 0.5 (the probability of heads).
, is assigned a number between zero and one, inclusive, and describes the proportion of time we expect the event to occur over the long-term. P(A) = 0 means the event A can never happen. P(A) = 1 means the event A always happens. P(A) = 0.5 means the event A is equally likely to occur or not to occur. For example, if you flip one fair coin repeatedly (from 20 to 2,000 to 20,000 times) the relative frequency of heads approaches 0.5 (the probability of heads). is 1 and the probability of the empty set is 0. This is: P(S) = 1 and P(∅) = 0.
is 1 and the probability of the empty set is 0. This is: P(S) = 1 and P(∅) = 0.

 as “the probability of A given B”.
as “the probability of A given B”. .
. .
. .
. are mutually independent if for any sub-collection
are mutually independent if for any sub-collection  there is:
there is:
 cards. It consists of four suits. The suits are clubs, diamonds, hearts and spades. There are
cards. It consists of four suits. The suits are clubs, diamonds, hearts and spades. There are  cards in each suit consisting of
cards in each suit consisting of  ,
,  (jack),
(jack),  (queen),
(queen),  (king) of that suit.
(king) of that suit. cards remaining in the deck. It is the three of diamonds. You put this card aside and pick the third card from the remaining
cards remaining in the deck. It is the three of diamonds. You put this card aside and pick the third card from the remaining  cards in the deck. The third card is the
cards in the deck. The third card is the 

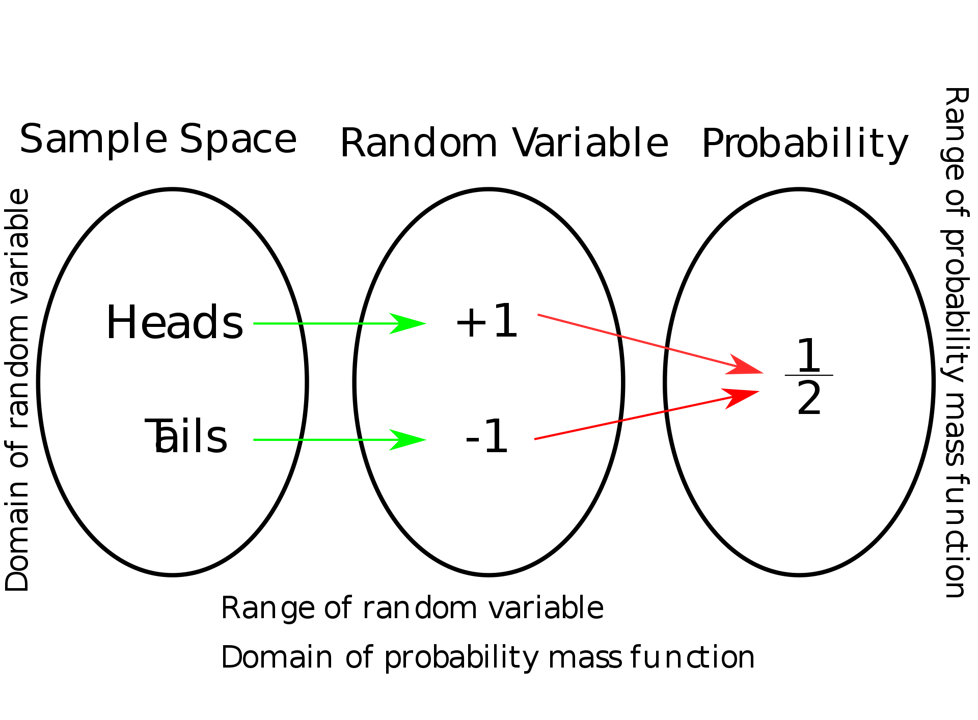
![{\displaystyle [0,1]\subseteq \mathbb {R} } {\displaystyle [0,1]\subseteq \mathbb {R} }](https://atu0g9ctah.execute-api.ca-central-1.amazonaws.com/latest/latex?latex=%7B%5Cdisplaystyle%20%5B0%2C1%5D%5Csubseteq%20%5Cmathbb%20%7BR%7D%20%7D&fg=000000&font=TeX&svg=1) , which provides the probability measure on the set of all possible values of the random variable. Random variables are shown as Roman capital letters, often towards the end of the alphabet, such as
, which provides the probability measure on the set of all possible values of the random variable. Random variables are shown as Roman capital letters, often towards the end of the alphabet, such as  .
. to a measurable space of
to a measurable space of  , where 1 is correspondent to H and -1 is correspondent to T, utilizing a random variable of
, where 1 is correspondent to H and -1 is correspondent to T, utilizing a random variable of  =
=  = +1, written as
= +1, written as  .
.
 for an event.
for an event. .
.![{\displaystyle F\colon \mathbb {R} \rightarrow [0,1]} {\displaystyle F\colon \mathbb {R} \rightarrow [0,1]}](https://atu0g9ctah.execute-api.ca-central-1.amazonaws.com/latest/latex?latex=%7B%5Cdisplaystyle%20F%5Ccolon%20%5Cmathbb%20%7BR%7D%20%5Crightarrow%20%5B0%2C1%5D%7D&fg=000000&font=TeX&svg=1) , where
, where  and
and  . Every function with these four properties is a CDF: for every such function, a random variable can be defined such that the function is the cumulative distribution function of that random variable.
. Every function with these four properties is a CDF: for every such function, a random variable can be defined such that the function is the cumulative distribution function of that random variable.![F(x)=P[X \leq x] F(x)=P[X \leq x]](https://atu0g9ctah.execute-api.ca-central-1.amazonaws.com/latest/latex?latex=F%28x%29%3DP%5BX%20%5Cleq%20x%5D&fg=000000&font=TeX&svg=1)

 ,
, ,…, is a non-negative function f (x ), with f (
,…, is a non-negative function f (x ), with f ( ) giving the probability that X takes the value
) giving the probability that X takes the value 
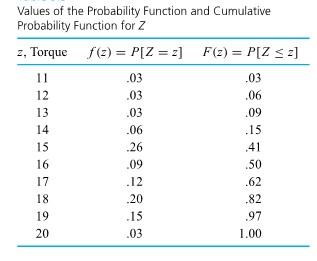
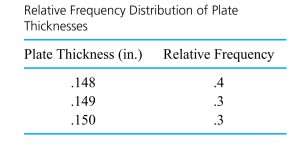
 = the next measured torque for bolt 3 (recorded to the nearest integer), and we will treat Z as a discrete random variable. Now we want to give a plausible probility function for it. The relative frequencies for the bolt 3 torque measurements recorded introduce the relative frequency distribution:
= the next measured torque for bolt 3 (recorded to the nearest integer), and we will treat Z as a discrete random variable. Now we want to give a plausible probility function for it. The relative frequencies for the bolt 3 torque measurements recorded introduce the relative frequency distribution:
 = the torque value selected.
= the torque value selected.
![F(16.3)=P[Z \leq 16.3]=P[Z \leq 16]=F(16)=.50 F(16.3)=P[Z \leq 16.3]=P[Z \leq 16]=F(16)=.50](https://atu0g9ctah.execute-api.ca-central-1.amazonaws.com/latest/latex?latex=F%2816.3%29%3DP%5BZ%20%5Cleq%2016.3%5D%3DP%5BZ%20%5Cleq%2016%5D%3DF%2816%29%3D.50&fg=000000&font=TeX&svg=1)
![F(32)=P[Z \leq 32]=1.00 F(32)=P[Z \leq 32]=1.00](https://atu0g9ctah.execute-api.ca-central-1.amazonaws.com/latest/latex?latex=F%2832%29%3DP%5BZ%20%5Cleq%2032%5D%3D1.00&fg=000000&font=TeX&svg=1)




 . Often the notation
. Often the notation  is used in place of Var X, and
is used in place of Var X, and  = 2.15 ft lb
= 2.15 ft lb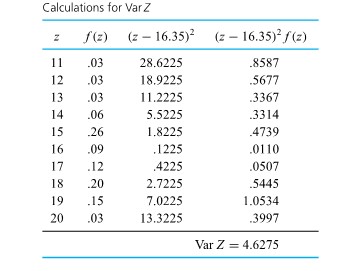
 .
.



![X[latex] has the <strong>binomial (n, p) distribution</strong>.</div> <div> <div> <div class="textbox"> <strong>DEFINITION 3.2.5.1. Binomial Definition</strong> The binomial [latex](n, p) X[latex] has the <strong>binomial (n, p) distribution</strong>.</div> <div> <div> <div class="textbox"> <strong>DEFINITION 3.2.5.1. Binomial Definition</strong> The binomial [latex](n, p)](https://atu0g9ctah.execute-api.ca-central-1.amazonaws.com/latest/latex?latex=X%5Blatex%5D%20has%20the%20%3Cstrong%3Ebinomial%20%28n%2C%20p%29%20distribution%3C%2Fstrong%3E.%3C%2Fdiv%3E%20%20%3Cdiv%3E%20%20%3Cdiv%3E%20%20%3Cdiv%20class%3D%22textbox%22%3E%20%20%20%20%3Cstrong%3EDEFINITION%203.2.5.1.%20Binomial%20Definition%3C%2Fstrong%3E%20%20%20%20The%20binomial%20%5Blatex%5D%28n%2C%20p%29&fg=000000&font=TeX&svg=1) distribution is a discrete probability distribution with probability function
distribution is a discrete probability distribution with probability function 
 .
. for each trial producing a no go/failure outcome. And the
for each trial producing a no go/failure outcome. And the  term is a count of the number of patterns in which it would be possible to see
term is a count of the number of patterns in which it would be possible to see  nomial distribution derives from the fact that the values
nomial distribution derives from the fact that the values  are the terms in the expansion of
are the terms in the expansion of
 , the resulting histogram is right-skewed. For
, the resulting histogram is right-skewed. For  , the resulting histogram is left-skewed. The skewness increases as
, the resulting histogram is left-skewed. The skewness increases as 
 is indeed a sensible figure for the chance that a given shaft will be reworkable. Suppose further that
is indeed a sensible figure for the chance that a given shaft will be reworkable. Suppose further that 
![\begin{aligned}P[\text { at least two reworkable shafts] } & =P[U \geq 2] \\& =f(2)+f(3)+\cdots+f(10) \\& =1-(f(0)+f(1)) \\& =1-\left(\frac{10 !}{0 ! 10 !}(.2)^{0}(.8)^{10}+\frac{10 !}{1 ! 9 !}(.2)^{1}(.8)^{9}\right) \\&=.62\end{aligned} \begin{aligned}P[\text { at least two reworkable shafts] } & =P[U \geq 2] \\& =f(2)+f(3)+\cdots+f(10) \\& =1-(f(0)+f(1)) \\& =1-\left(\frac{10 !}{0 ! 10 !}(.2)^{0}(.8)^{10}+\frac{10 !}{1 ! 9 !}(.2)^{1}(.8)^{9}\right) \\&=.62\end{aligned}](https://atu0g9ctah.execute-api.ca-central-1.amazonaws.com/latest/latex?latex=%5Cbegin%7Baligned%7DP%5B%5Ctext%20%7B%20at%20least%20two%20reworkable%20shafts%5D%20%7D%20%26%20%3DP%5BU%20%5Cgeq%202%5D%20%5C%5C%26%20%3Df%282%29%2Bf%283%29%2B%5Ccdots%2Bf%2810%29%20%5C%5C%26%20%3D1-%28f%280%29%2Bf%281%29%29%20%5C%5C%26%20%3D1-%5Cleft%28%5Cfrac%7B10%20%21%7D%7B0%20%21%2010%20%21%7D%28.2%29%5E%7B0%7D%28.8%29%5E%7B10%7D%2B%5Cfrac%7B10%20%21%7D%7B1%20%21%209%20%21%7D%28.2%29%5E%7B1%7D%28.8%29%5E%7B9%7D%5Cright%29%20%5C%5C%26%3D.62%5Cend%7Baligned%7D&fg=000000&font=TeX&svg=1)
 's have to sum up to 1 , is a common and useful one.)
's have to sum up to 1 , is a common and useful one.) , and the . 62 figure largely irrelevant. (The independence-of-trials assumption would be inappropriate in this situation.)
, and the . 62 figure largely irrelevant. (The independence-of-trials assumption would be inappropriate in this situation.)
 .
. from it.
from it.
 is obtained as follows. Possible values for
is obtained as follows. Possible values for ![\begin{aligned}f(0)= & P[V=0] \\= & P[\text { first pellet selected is nonconforming and } \\& \text { subsequently the second pellet is also nonconforming }] \\f(2)= & P[V=2] \\= & P[\text { first pellet selected is conforming and } \\& \text { subsequently the second pellet selected is conforming }] \\f(1)= & 1-(f(0)+f(2))\end{aligned} \begin{aligned}f(0)= & P[V=0] \\= & P[\text { first pellet selected is nonconforming and } \\& \text { subsequently the second pellet is also nonconforming }] \\f(2)= & P[V=2] \\= & P[\text { first pellet selected is conforming and } \\& \text { subsequently the second pellet selected is conforming }] \\f(1)= & 1-(f(0)+f(2))\end{aligned}](https://atu0g9ctah.execute-api.ca-central-1.amazonaws.com/latest/latex?latex=%5Cbegin%7Baligned%7Df%280%29%3D%20%26%20P%5BV%3D0%5D%20%5C%5C%3D%20%26%20P%5B%5Ctext%20%7B%20first%20pellet%20selected%20is%20nonconforming%20and%20%7D%20%5C%5C%26%20%5Ctext%20%7B%20subsequently%20the%20second%20pellet%20is%20also%20nonconforming%20%7D%5D%20%5C%5Cf%282%29%3D%20%26%20P%5BV%3D2%5D%20%5C%5C%3D%20%26%20P%5B%5Ctext%20%7B%20first%20pellet%20selected%20is%20conforming%20and%20%7D%20%5C%5C%26%20%5Ctext%20%7B%20subsequently%20the%20second%20pellet%20selected%20is%20conforming%20%7D%5D%20%5C%5Cf%281%29%3D%20%26%201-%28f%280%29%2Bf%282%29%29%5Cend%7Baligned%7D&fg=000000&font=TeX&svg=1)
 is
is


 to
to  . Nevertheless, for most practical purposes,
. Nevertheless, for most practical purposes,  . To see this, note that
. To see this, note that
 is not too extreme, and a binomial distribution is a decent description of a variable arising from simple random sampling.
is not too extreme, and a binomial distribution is a decent description of a variable arising from simple random sampling.


 distribution
distribution
 .
. . One is then led to the binomial
. One is then led to the binomial  ) distribution. In fact, for large
) distribution. In fact, for large  probability function approximates the one specified in equation (5.10). So one might think of the Poisson distribution for counts as arising through a mechanism that would present many tiny similar opportunities for independent occurrence or non-occurrence throughout an interval of time or space.
probability function approximates the one specified in equation (5.10). So one might think of the Poisson distribution for counts as arising through a mechanism that would present many tiny similar opportunities for independent occurrence or non-occurrence throughout an interval of time or space.
 , whose probability histograms peak near their respective
, whose probability histograms peak near their respective 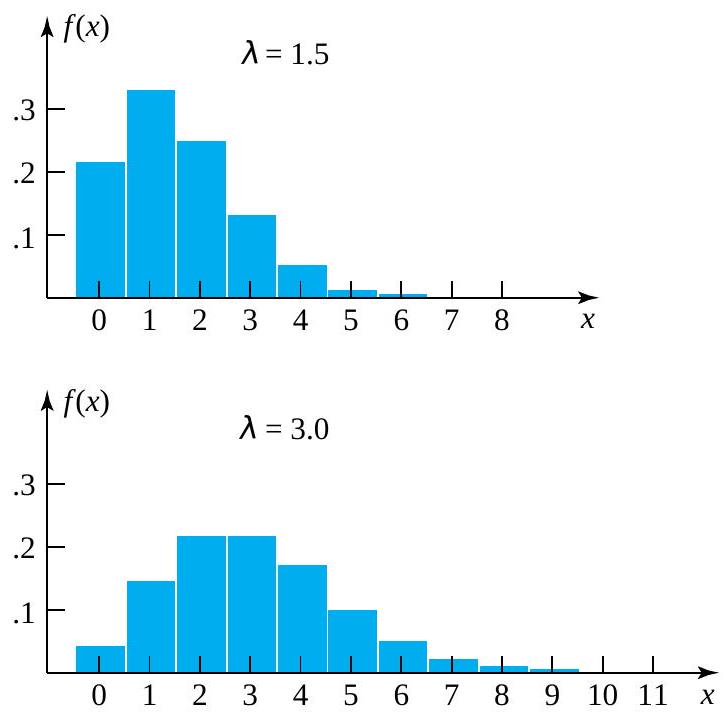


 -Particles
-Particles .
.

 [at least 4 particles are recorded]
[at least 4 particles are recorded]![=P[S \geq 4] =P[S \geq 4]](https://atu0g9ctah.execute-api.ca-central-1.amazonaws.com/latest/latex?latex=%3DP%5BS%20%5Cgeq%204%5D&fg=000000&font=TeX&svg=1)





 , the reasonable choice of
, the reasonable choice of 

![\begin{aligned}P[10 \leq M \leq 15]= & f(10)+f(11)+f(12)+f(13)+f(14)+f(15) \\= & \frac{e^{-12.5}(12.5)^{10}}{10 !}+\frac{e^{-12.5}(12.5)^{11}}{11 !}+\frac{e^{-12.5}(12.5)^{12}}{12 !} \\& +\frac{e^{-12.5}(12.5)^{13}}{13 !}+\frac{e^{-12.5}(12.5)^{14}}{14 !}+\frac{e^{-12.5}(12.5)^{15}}{15 !} \\= & .60\end{aligned} \begin{aligned}P[10 \leq M \leq 15]= & f(10)+f(11)+f(12)+f(13)+f(14)+f(15) \\= & \frac{e^{-12.5}(12.5)^{10}}{10 !}+\frac{e^{-12.5}(12.5)^{11}}{11 !}+\frac{e^{-12.5}(12.5)^{12}}{12 !} \\& +\frac{e^{-12.5}(12.5)^{13}}{13 !}+\frac{e^{-12.5}(12.5)^{14}}{14 !}+\frac{e^{-12.5}(12.5)^{15}}{15 !} \\= & .60\end{aligned}](https://atu0g9ctah.execute-api.ca-central-1.amazonaws.com/latest/latex?latex=%5Cbegin%7Baligned%7DP%5B10%20%5Cleq%20M%20%5Cleq%2015%5D%3D%20%26%20f%2810%29%2Bf%2811%29%2Bf%2812%29%2Bf%2813%29%2Bf%2814%29%2Bf%2815%29%20%5C%5C%3D%20%26%20%5Cfrac%7Be%5E%7B-12.5%7D%2812.5%29%5E%7B10%7D%7D%7B10%20%21%7D%2B%5Cfrac%7Be%5E%7B-12.5%7D%2812.5%29%5E%7B11%7D%7D%7B11%20%21%7D%2B%5Cfrac%7Be%5E%7B-12.5%7D%2812.5%29%5E%7B12%7D%7D%7B12%20%21%7D%20%5C%5C%26%20%2B%5Cfrac%7Be%5E%7B-12.5%7D%2812.5%29%5E%7B13%7D%7D%7B13%20%21%7D%2B%5Cfrac%7Be%5E%7B-12.5%7D%2812.5%29%5E%7B14%7D%7D%7B14%20%21%7D%2B%5Cfrac%7Be%5E%7B-12.5%7D%2812.5%29%5E%7B15%7D%7D%7B15%20%21%7D%20%5C%5C%3D%20%26%20.60%5Cend%7Baligned%7D&fg=000000&font=TeX&svg=1)

 = 1
= 1
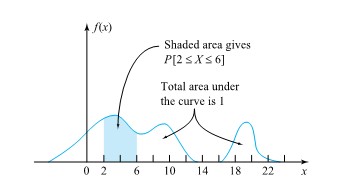
 to represent the curve.
to represent the curve.  f (x ) dx values as dx gets small. (In mechanics,
f (x ) dx values as dx gets small. (In mechanics,  X
X f(t) dt
f(t) dt F(x) = f(x)
F(x) = f(x)
 and
and  . P(c<x<d) is the area under the curve, above the x-axis, to the right of
. P(c<x<d) is the area under the curve, above the x-axis, to the right of  . The probability that
. The probability that  and
and  ). Since the probability is equal to the area, the probability is also zero.
). Since the probability is equal to the area, the probability is also zero. because probability is equal to area.
because probability is equal to area. .
.
 is used in place of Var X ,and σ is used in place of
is used in place of Var X ,and σ is used in place of 


 (remember that the standard deviation =
(remember that the standard deviation =  = σ). Figure 4.1.3.1 shows the notation for the standard normal distribution, and that the distribution shape depends on these parameters. Since the area under the curve must equal one, a change in the standard deviation, σ, causes a change in the shape of the curve; the curve becomes fatter or skinnier depending on σ. A change in μ causes the graph to shift to the left or right. This means there are an infinite number of normal probability distributions.
= σ). Figure 4.1.3.1 shows the notation for the standard normal distribution, and that the distribution shape depends on these parameters. Since the area under the curve must equal one, a change in the standard deviation, σ, causes a change in the shape of the curve; the curve becomes fatter or skinnier depending on σ. A change in μ causes the graph to shift to the left or right. This means there are an infinite number of normal probability distributions.

![P[a \leq X \leq b]=\int_a^b \frac{1}{\sqrt{2 \pi \sigma^2}} e^{-(x-\mu)^2 / 2 \sigma^2} d x=\int_{(a-\mu) / \sigma}^{(b-\mu) / \sigma} \frac{1}{\sqrt{2 \pi}} e^{-z^2 / 2} d z P[a \leq X \leq b]=\int_a^b \frac{1}{\sqrt{2 \pi \sigma^2}} e^{-(x-\mu)^2 / 2 \sigma^2} d x=\int_{(a-\mu) / \sigma}^{(b-\mu) / \sigma} \frac{1}{\sqrt{2 \pi}} e^{-z^2 / 2} d z](https://atu0g9ctah.execute-api.ca-central-1.amazonaws.com/latest/latex?latex=P%5Ba%20%5Cleq%20X%20%5Cleq%20b%5D%3D%5Cint_a%5Eb%20%5Cfrac%7B1%7D%7B%5Csqrt%7B2%20%5Cpi%20%5Csigma%5E2%7D%7D%20e%5E%7B-%28x-%5Cmu%29%5E2%20%2F%202%20%5Csigma%5E2%7D%20d%20x%3D%5Cint_%7B%28a-%5Cmu%29%20%2F%20%5Csigma%7D%5E%7B%28b-%5Cmu%29%20%2F%20%5Csigma%7D%20%5Cfrac%7B1%7D%7B%5Csqrt%7B2%20%5Cpi%7D%7D%20e%5E%7B-z%5E2%20%2F%202%7D%20d%20z&fg=000000&font=TeX&svg=1)


 and a value x associated with X , one converts to units of standard deviations above the mean via:
and a value x associated with X , one converts to units of standard deviations above the mean via: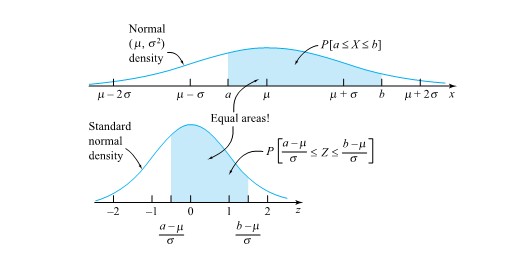

 is used to stand for the standard normal cumulative probability function, instead of the more generic F.
is used to stand for the standard normal cumulative probability function, instead of the more generic F. , the standard normal quantile function,
, the standard normal quantile function,
 is not just a standard normal phenomenon but is true in general
is not just a standard normal phenomenon but is true in general

 = .025 in the right tail of the standard normal
= .025 in the right tail of the standard normal = .975. Locating .975 in the table body, one sees that z = 1.96.
= .975. Locating .975 in the table body, one sees that z = 1.96.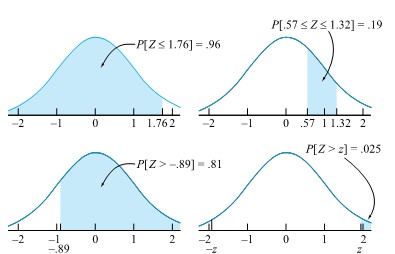


 = 134.0 and w
= 134.0 and w = 136.0 are converted to z-values (or units of standard deviations above the mean) as
= 136.0 are converted to z-values (or units of standard deviations above the mean) as







 , giving the probability that (simultaneously)
, giving the probability that (simultaneously)  . That is,
. That is,![f(x, y)=P[X=x \text { and } Y=y] f(x, y)=P[X=x \text { and } Y=y]](https://atu0g9ctah.execute-api.ca-central-1.amazonaws.com/latest/latex?latex=f%28x%2C%20y%29%3DP%5BX%3Dx%20%5Ctext%20%7B%20and%20%7D%20Y%3Dy%5D&fg=000000&font=TeX&svg=1)
 the next torque recorded for bolt 3
the next torque recorded for bolt 3 the next torque recorded for bolt 4
the next torque recorded for bolt 4 and
and ![Y=18] Y=18]](https://atu0g9ctah.execute-api.ca-central-1.amazonaws.com/latest/latex?latex=Y%3D18%5D&fg=000000&font=TeX&svg=1) might be
might be  , the relative frequency of this pair in the data set. Similarly, the assignments
, the relative frequency of this pair in the data set. Similarly, the assignments![\begin{aligned}& P[X=18 \text { and } Y=17]=\frac{2}{34} \\& P[X=14 \text { and } Y=9]=0\end{aligned} \begin{aligned}& P[X=18 \text { and } Y=17]=\frac{2}{34} \\& P[X=14 \text { and } Y=9]=0\end{aligned}](https://atu0g9ctah.execute-api.ca-central-1.amazonaws.com/latest/latex?latex=%5Cbegin%7Baligned%7D%26%20P%5BX%3D18%20%5Ctext%20%7B%20and%20%7D%20Y%3D17%5D%3D%5Cfrac%7B2%7D%7B34%7D%20%5C%5C%26%20P%5BX%3D14%20%5Ctext%20%7B%20and%20%7D%20Y%3D9%5D%3D0%5Cend%7Baligned%7D&fg=000000&font=TeX&svg=1)

![[0,1] [0,1]](https://atu0g9ctah.execute-api.ca-central-1.amazonaws.com/latest/latex?latex=%5B0%2C1%5D&fg=000000&font=TeX&svg=1) and that they total to 1 . By summing up just some of the
and that they total to 1 . By summing up just some of the ![\begin{aligned}& P[X\geq Y], \\& P[|X-Y|\leq 1], \\& \text { and } P[X=17]\end{aligned} \begin{aligned}& P[X\geq Y], \\& P[|X-Y|\leq 1], \\& \text { and } P[X=17]\end{aligned}](https://atu0g9ctah.execute-api.ca-central-1.amazonaws.com/latest/latex?latex=%5Cbegin%7Baligned%7D%26%20P%5BX%5Cgeq%20Y%5D%2C%20%5C%5C%26%20P%5B%7CX-Y%7C%5Cleq%201%5D%2C%20%5C%5C%26%20%5Ctext%20%7B%20and%20%7D%20P%5BX%3D17%5D%5Cend%7Baligned%7D&fg=000000&font=TeX&svg=1)
![P[X \geq Y] P[X \geq Y]](https://atu0g9ctah.execute-api.ca-central-1.amazonaws.com/latest/latex?latex=P%5BX%20%5Cgeq%20Y%5D&fg=000000&font=TeX&svg=1) , the probability that the measured bolt 3 torque is at least as big as the measured bolt 4 torque. Figure 4.2.1.1 indicates with asterisks which possible combinations of
, the probability that the measured bolt 3 torque is at least as big as the measured bolt 4 torque. Figure 4.2.1.1 indicates with asterisks which possible combinations of ![\begin{aligned}P[X \geq Y]= & f(15,13)+f(15,14)+f(15,15)+f(16,16) \\& +f(17,17)+f(18,14)+f(18,17)+f(18,18) \\& +f(19,16)+f(19,18)+f(20,20) \\= & \frac{1}{34}+\frac{1}{34}+\frac{3}{34}+\frac{2}{34}+\cdots+\frac{1}{34}=\frac{17}{34}\end{aligned} \begin{aligned}P[X \geq Y]= & f(15,13)+f(15,14)+f(15,15)+f(16,16) \\& +f(17,17)+f(18,14)+f(18,17)+f(18,18) \\& +f(19,16)+f(19,18)+f(20,20) \\= & \frac{1}{34}+\frac{1}{34}+\frac{3}{34}+\frac{2}{34}+\cdots+\frac{1}{34}=\frac{17}{34}\end{aligned}](https://atu0g9ctah.execute-api.ca-central-1.amazonaws.com/latest/latex?latex=%5Cbegin%7Baligned%7DP%5BX%20%5Cgeq%20Y%5D%3D%20%26%20f%2815%2C13%29%2Bf%2815%2C14%29%2Bf%2815%2C15%29%2Bf%2816%2C16%29%20%5C%5C%26%20%2Bf%2817%2C17%29%2Bf%2818%2C14%29%2Bf%2818%2C17%29%2Bf%2818%2C18%29%20%5C%5C%26%20%2Bf%2819%2C16%29%2Bf%2819%2C18%29%2Bf%2820%2C20%29%20%5C%5C%3D%20%26%20%5Cfrac%7B1%7D%7B34%7D%2B%5Cfrac%7B1%7D%7B34%7D%2B%5Cfrac%7B3%7D%7B34%7D%2B%5Cfrac%7B2%7D%7B34%7D%2B%5Ccdots%2B%5Cfrac%7B1%7D%7B34%7D%3D%5Cfrac%7B17%7D%7B34%7D%5Cend%7Baligned%7D&fg=000000&font=TeX&svg=1)
![P[|X-Y| \leq 1] P[|X-Y| \leq 1]](https://atu0g9ctah.execute-api.ca-central-1.amazonaws.com/latest/latex?latex=P%5B%7CX-Y%7C%20%5Cleq%201%5D&fg=000000&font=TeX&svg=1) -the probability that the bolt 3 and 4 torques are within
-the probability that the bolt 3 and 4 torques are within  of each other. Figure 4.2.1.2 shows combinations of
of each other. Figure 4.2.1.2 shows combinations of ![\begin{aligned}P[|X-Y| \leq 1]= & f(15,14)+f(15,15)+f(15,16)+f(16,16) \\& +f(16,17)+f(17,17)+f(17,18)+f(18,17) \\& +f(18,18)+f(19,18)+f(19,20)+f(20,20)=\frac{18}{34}\end{aligned} \begin{aligned}P[|X-Y| \leq 1]= & f(15,14)+f(15,15)+f(15,16)+f(16,16) \\& +f(16,17)+f(17,17)+f(17,18)+f(18,17) \\& +f(18,18)+f(19,18)+f(19,20)+f(20,20)=\frac{18}{34}\end{aligned}](https://atu0g9ctah.execute-api.ca-central-1.amazonaws.com/latest/latex?latex=%5Cbegin%7Baligned%7DP%5B%7CX-Y%7C%20%5Cleq%201%5D%3D%20%26%20f%2815%2C14%29%2Bf%2815%2C15%29%2Bf%2815%2C16%29%2Bf%2816%2C16%29%20%5C%5C%26%20%2Bf%2816%2C17%29%2Bf%2817%2C17%29%2Bf%2817%2C18%29%2Bf%2818%2C17%29%20%5C%5C%26%20%2Bf%2818%2C18%29%2Bf%2819%2C18%29%2Bf%2819%2C20%29%2Bf%2820%2C20%29%3D%5Cfrac%7B18%7D%7B34%7D%5Cend%7Baligned%7D&fg=000000&font=TeX&svg=1)
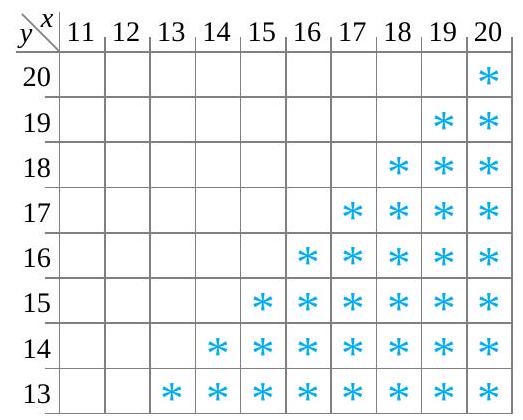

![P[X=17] P[X=17]](https://atu0g9ctah.execute-api.ca-central-1.amazonaws.com/latest/latex?latex=P%5BX%3D17%5D&fg=000000&font=TeX&svg=1) , the probability that the measured bolt 3 torque is
, the probability that the measured bolt 3 torque is  , is obtained by adding down the
, is obtained by adding down the  column in Table 4.2.1.1. That is,
column in Table 4.2.1.1. That is,![\begin{aligned} P[X=17] & =f(17,17)+f(17,18)+f(17,19) \\ & =\frac{1}{34}+\frac{1}{34}+\frac{2}{34} \\ & =\frac{4}{34} \end{aligned} \begin{aligned} P[X=17] & =f(17,17)+f(17,18)+f(17,19) \\ & =\frac{1}{34}+\frac{1}{34}+\frac{2}{34} \\ & =\frac{4}{34} \end{aligned}](https://atu0g9ctah.execute-api.ca-central-1.amazonaws.com/latest/latex?latex=%5Cbegin%7Baligned%7D%20P%5BX%3D17%5D%20%26%20%3Df%2817%2C17%29%2Bf%2817%2C18%29%2Bf%2817%2C19%29%20%5C%5C%20%26%20%3D%5Cfrac%7B1%7D%7B34%7D%2B%5Cfrac%7B1%7D%7B34%7D%2B%5Cfrac%7B2%7D%7B34%7D%20%5C%5C%20%26%20%3D%5Cfrac%7B4%7D%7B34%7D%20%5Cend%7Baligned%7D&fg=000000&font=TeX&svg=1)
 . And one can add across rows in the same table to get values for the probability function of
. And one can add across rows in the same table to get values for the probability function of  . One can then write these sums in the margins of the two-way table. So it should not be surprising that probability distributions for individual random variables obtained from their joint distribution are called marginal distributions. A formal statement of this terminology in the case of two discrete variables is next.
. One can then write these sums in the margins of the two-way table. So it should not be surprising that probability distributions for individual random variables obtained from their joint distribution are called marginal distributions. A formal statement of this terminology in the case of two discrete variables is next.



 and
and  are known, is there then exactly one choice for
are known, is there then exactly one choice for 
 torque situation, a technician who has just loosened bolt 3 and measured the torque as
torque situation, a technician who has just loosened bolt 3 and measured the torque as  ought to have expectations for bolt 4 torque
ought to have expectations for bolt 4 torque  somewhat different from those described by the marginal distribution in Table 4.2.1.3. After all, returning to the data in that led to Table 4.2.1.1, the relative frequency distribution of bolt 4 torques for those components with bolt 3 torque of
somewhat different from those described by the marginal distribution in Table 4.2.1.3. After all, returning to the data in that led to Table 4.2.1.1, the relative frequency distribution of bolt 4 torques for those components with bolt 3 torque of  ought to make a probability distribution for
ought to make a probability distribution for 
 is the function of
is the function of 
 given
given  is the function of
is the function of 


 ), so that they are renormalized to total to 1 . Similarly, equation (4.2.2.3) says that looking only at the column specified by
), so that they are renormalized to total to 1 . Similarly, equation (4.2.2.3) says that looking only at the column specified by  , the appropriate conditional distribution for
, the appropriate conditional distribution for 
 . So dividing values in the
. So dividing values in the 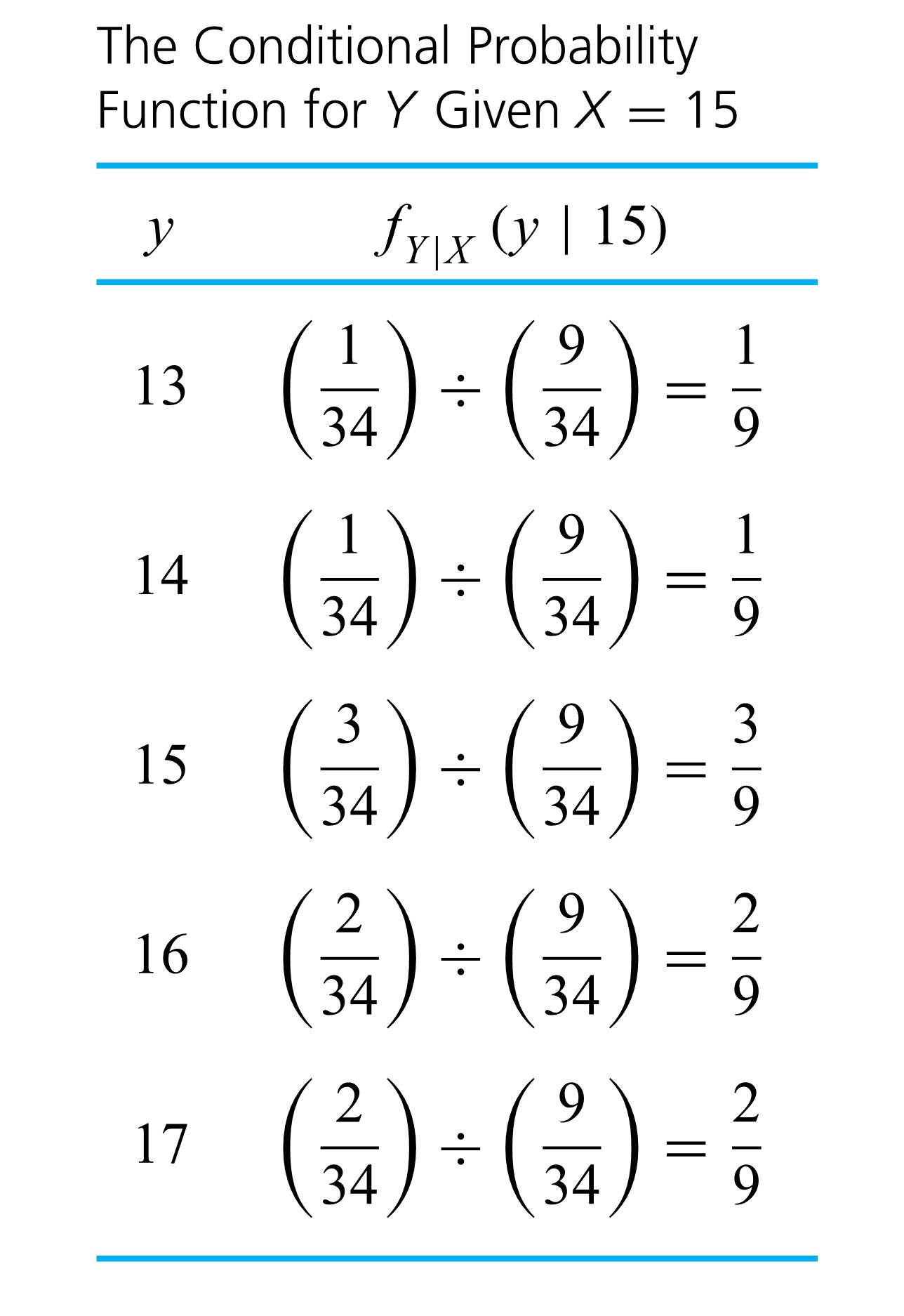
 specified by
specified by
 , shown in Table 4.2.2.3 . Tables 4.2.2.2 and 4.2.4.3 confirm that the conditional distributions of
, shown in Table 4.2.2.3 . Tables 4.2.2.2 and 4.2.4.3 confirm that the conditional distributions of 
 . In this situation, equation (4.2.2.2) gives
. In this situation, equation (4.2.2.2) gives
 row of Table 4.2.1..2 divided by the marginal
row of Table 4.2.1..2 divided by the marginal  is given in Table 4.2.2.4.
is given in Table 4.2.2.4.
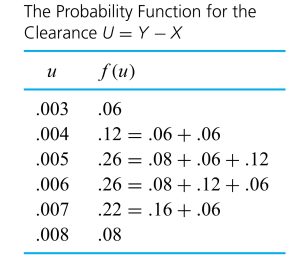
 provides some information about
provides some information about 

 and
and 




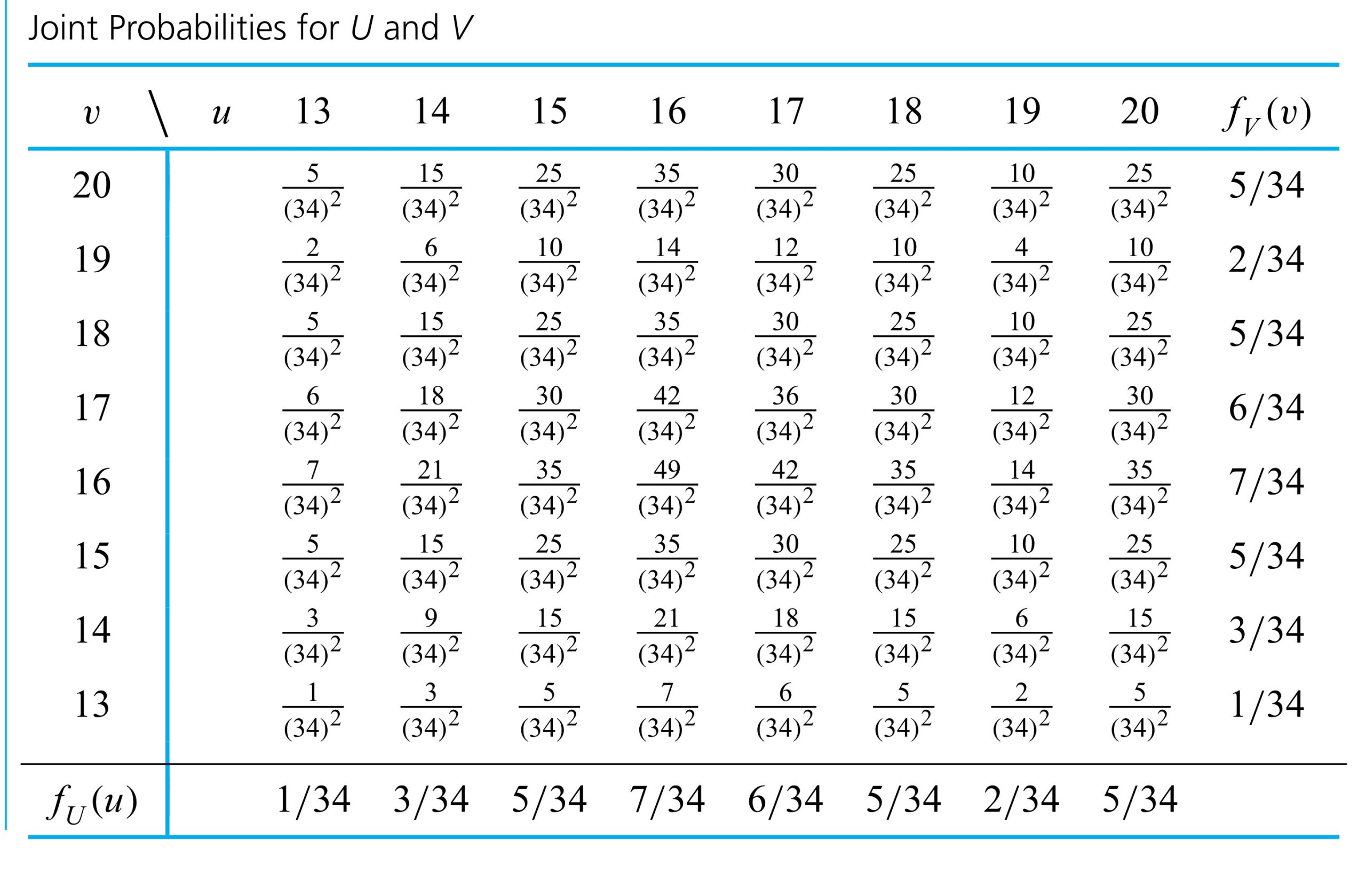

 , one clearly wants
, one clearly wants![f(13,13)=P[U=13 \text { and } V=13]=0 f(13,13)=P[U=13 \text { and } V=13]=0](https://atu0g9ctah.execute-api.ca-central-1.amazonaws.com/latest/latex?latex=f%2813%2C13%29%3DP%5BU%3D13%20%5Ctext%20%7B%20and%20%7D%20V%3D13%5D%3D0&fg=000000&font=TeX&svg=1)



 slips labeled with torques with relative frequencies as in Table 4.2.2.6. Then even if sampling is done without replacement, the probabilities developed earlier for
slips labeled with torques with relative frequencies as in Table 4.2.2.6. Then even if sampling is done without replacement, the probabilities developed earlier for 





 is much larger than the sample size
is much larger than the sample size  all have the same marginal distribution and are independent, they are termed iid or independent and identically distributed.
all have the same marginal distribution and are independent, they are termed iid or independent and identically distributed. , the object is to predict the behavior of the random variable
, the object is to predict the behavior of the random variable

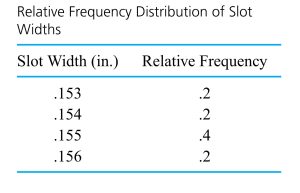

 are
are  are
are  constants, then the random variable
constants, then the random variable  has mean
has mean

 and the other
and the other  ‘s equal to plus and minus 1 ‘s.
‘s equal to plus and minus 1 ‘s. , and
, and 


 and [/latex]\operatorname{Var} U[/latex], there is no need to go through the intermediate step of deriving the distribution of
and [/latex]\operatorname{Var} U[/latex], there is no need to go through the intermediate step of deriving the distribution of  . That is, in cases where random variables
. That is, in cases where random variables 
 and
and 
![\begin{aligned}\operatorname{Var} \bar{X} & =\left(\frac{1}{n}\right)^{2} \operatorname{Var} X_{1}+\left(\frac{1}{n}\right)^{2} \operatorname{Var} X_{2}+\cdots+\left(\frac{1}{n}\right)^{2} \operatorname{Var} X_{n} \\& =n\left(\frac{1}{n}\right)^{2} \sigma^{2}=\frac{\sigma^{2}}{n}\end{aligned}</div> </div></blockquote> <div>.</div> <div>Since [latex]\sigma^{2} / n \begin{aligned}\operatorname{Var} \bar{X} & =\left(\frac{1}{n}\right)^{2} \operatorname{Var} X_{1}+\left(\frac{1}{n}\right)^{2} \operatorname{Var} X_{2}+\cdots+\left(\frac{1}{n}\right)^{2} \operatorname{Var} X_{n} \\& =n\left(\frac{1}{n}\right)^{2} \sigma^{2}=\frac{\sigma^{2}}{n}\end{aligned}</div> </div></blockquote> <div>.</div> <div>Since [latex]\sigma^{2} / n](https://atu0g9ctah.execute-api.ca-central-1.amazonaws.com/latest/latex?latex=%5Cbegin%7Baligned%7D%5Coperatorname%7BVar%7D%20%5Cbar%7BX%7D%20%26%20%3D%5Cleft%28%5Cfrac%7B1%7D%7Bn%7D%5Cright%29%5E%7B2%7D%20%5Coperatorname%7BVar%7D%20X_%7B1%7D%2B%5Cleft%28%5Cfrac%7B1%7D%7Bn%7D%5Cright%29%5E%7B2%7D%20%5Coperatorname%7BVar%7D%20X_%7B2%7D%2B%5Ccdots%2B%5Cleft%28%5Cfrac%7B1%7D%7Bn%7D%5Cright%29%5E%7B2%7D%20%5Coperatorname%7BVar%7D%20X_%7Bn%7D%20%5C%5C%26%20%3Dn%5Cleft%28%5Cfrac%7B1%7D%7Bn%7D%5Cright%29%5E%7B2%7D%20%5Csigma%5E%7B2%7D%3D%5Cfrac%7B%5Csigma%5E%7B2%7D%7D%7Bn%7D%5Cend%7Baligned%7D%3C%2Fdiv%3E%20%20%3C%2Fdiv%3E%3C%2Fblockquote%3E%20%20%3Cdiv%3E.%3C%2Fdiv%3E%20%20%3Cdiv%3ESince%20%5Blatex%5D%5Csigma%5E%7B2%7D%20%2F%20n&fg=000000&font=TeX&svg=1) is decreasing in
is decreasing in  having a probability distribution centered at the population mean
having a probability distribution centered at the population mean ![\bar{X}/[latex] under random sampling with replacement, are also approximate descriptions of the behavior of [latex]\bar{X} \bar{X}/[latex] under random sampling with replacement, are also approximate descriptions of the behavior of [latex]\bar{X}](https://atu0g9ctah.execute-api.ca-central-1.amazonaws.com/latest/latex?latex=%5Cbar%7BX%7D%2F%5Blatex%5D%20under%20random%20sampling%20with%20replacement%2C%20are%20also%20approximate%20descriptions%20of%20the%20behavior%20of%20%5Blatex%5D%5Cbar%7BX%7D&fg=000000&font=TeX&svg=1) under simple random sampling in enumerative contexts. (Recall the discussion about the approximate independence of observations resulting from simple random sampling of large populations.)
under simple random sampling in enumerative contexts. (Recall the discussion about the approximate independence of observations resulting from simple random sampling of large populations.) .)
.) the last digit of the serial number observed next Monday at 9 A.M.
the last digit of the serial number observed next Monday at 9 A.M. the last digit of the serial number observed the following Monday at 9 A.M.
the last digit of the serial number observed the following Monday at 9 A.M. is that they are independent, each with the marginal probability function
is that they are independent, each with the marginal probability function
 has the probability function given in Table 4.2.2.1 and pictured in Figure 4.2.2.2
has the probability function given in Table 4.2.2.1 and pictured in Figure 4.2.2.2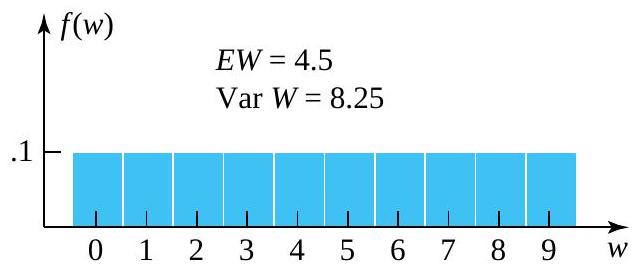
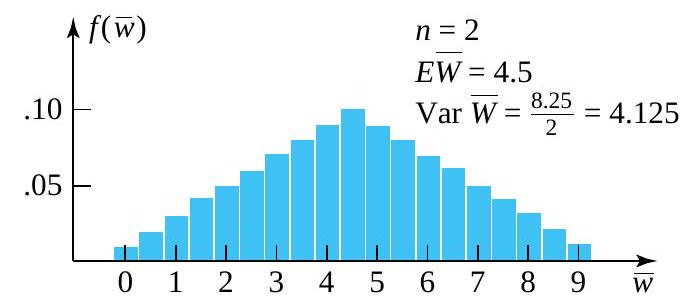
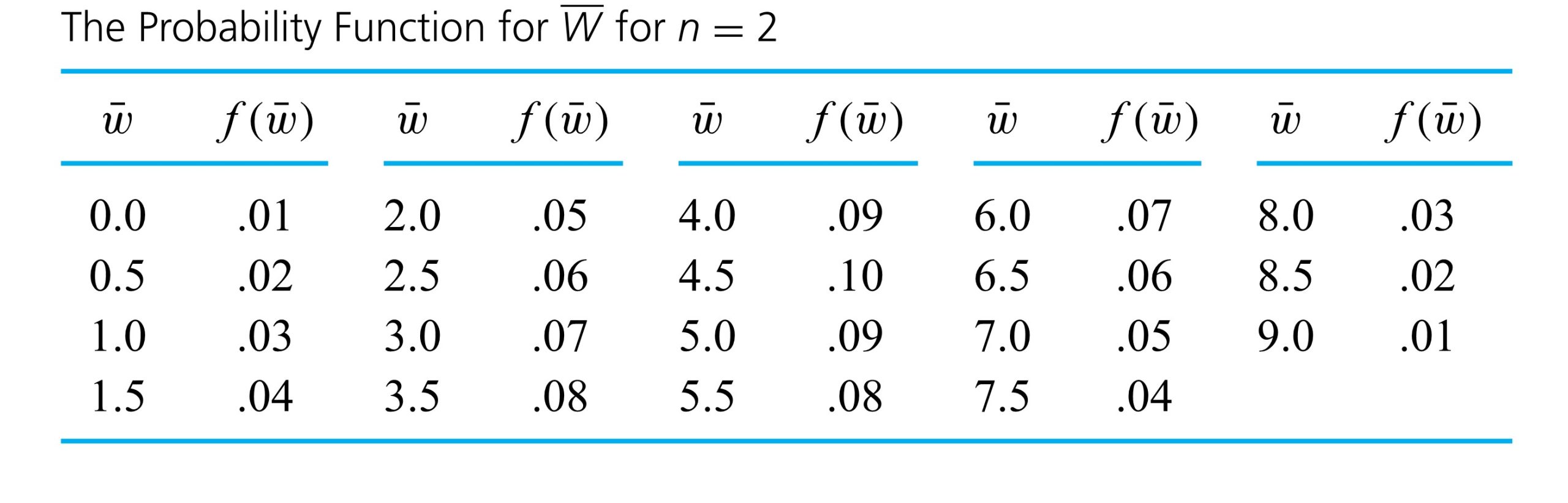
 and the small sample size of
and the small sample size of  looks far more bell-shaped than the underlying distribution. It is clear why this is so. As you move away from the mean or central value of
looks far more bell-shaped than the underlying distribution. It is clear why this is so. As you move away from the mean or central value of  and
and  that can produce a given value of
that can produce a given value of  . For example, to observe
. For example, to observe  , you must have
, you must have  and
and  -that is, you must observe not one but two extreme values. On the other hand, there are ten different combinations of
-that is, you must observe not one but two extreme values. On the other hand, there are ten different combinations of  .
. (with marginal distribution were simulated and each set averaged to produce 1,000 simulated values of
(with marginal distribution were simulated and each set averaged to produce 1,000 simulated values of  . Figure 4.2.2.3 is a histogram of these 1,000 values. Notice the bell-shaped character of the plot. (The simulated mean of
. Figure 4.2.2.3 is a histogram of these 1,000 values. Notice the bell-shaped character of the plot. (The simulated mean of  , while the variance of
, while the variance of  , in close agreement with formulas.)
, in close agreement with formulas.)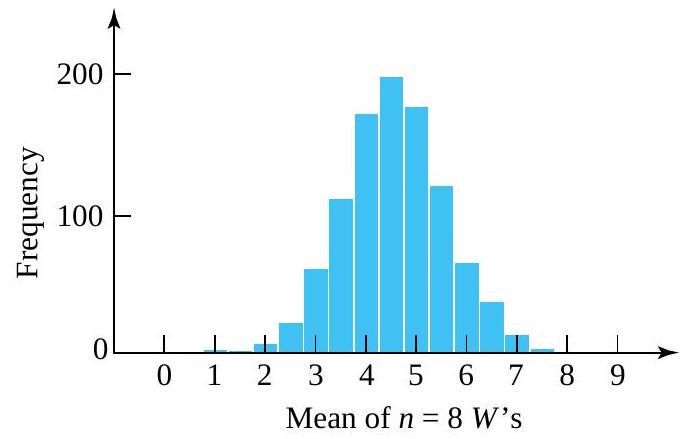
 or so is adequate to make
or so is adequate to make  excess service times, to produce
excess service times, to produce the sample mean time (over a
the sample mean time (over a  threshold) required to complete the next 100 stamp sales
threshold) required to complete the next 100 stamp sales![P[\bar{S}>17] P[\bar{S}>17]](https://atu0g9ctah.execute-api.ca-central-1.amazonaws.com/latest/latex?latex=P%5B%5Cbar%7BS%7D%3E17%5D&fg=000000&font=TeX&svg=1) .
. distribution is plausible for the individual excess service times,
distribution is plausible for the individual excess service times, 

 , via formulas. Further, in view of the fact that
, via formulas. Further, in view of the fact that 
 -values before consulting the standard normal table. In this case, the mean and standard deviation to be used are (respectively)
-values before consulting the standard normal table. In this case, the mean and standard deviation to be used are (respectively)  and
and  . That is, a
. That is, a 
![P[\bar{S}>17] \approx P[Z>.30]=1-\Phi(.30)=.38 P[\bar{S}>17] \approx P[Z>.30]=1-\Phi(.30)=.38](https://atu0g9ctah.execute-api.ca-central-1.amazonaws.com/latest/latex?latex=P%5B%5Cbar%7BS%7D%3E17%5D%20%5Capprox%20P%5BZ%3E.30%5D%3D1-%5CPhi%28.30%29%3D.38&fg=000000&font=TeX&svg=1)





 .3 g
.3 g







 < z
< z





![P\left[\bar{x}-1.645 \frac{s}{\sqrt{n}}<\mu<\bar{x}+1.645 \frac{s}{\sqrt{n}}\right] \approx .90 P\left[\bar{x}-1.645 \frac{s}{\sqrt{n}}<\mu<\bar{x}+1.645 \frac{s}{\sqrt{n}}\right] \approx .90](https://atu0g9ctah.execute-api.ca-central-1.amazonaws.com/latest/latex?latex=P%5Cleft%5B%5Cbar%7Bx%7D-1.645%20%5Cfrac%7Bs%7D%7B%5Csqrt%7Bn%7D%7D%3C%5Cmu%3C%5Cbar%7Bx%7D%2B1.645%20%5Cfrac%7Bs%7D%7B%5Csqrt%7Bn%7D%7D%5Cright%5D%20%5Capprox%20.90&fg=000000&font=TeX&svg=1)
 . Setting
. Setting





 .
.
 .It is of the same form as the corresponding null hypothesis, except that the equality sign
.It is of the same form as the corresponding null hypothesis, except that the equality sign


 itself. Using form (5.1.2.4), the reference distribution will always be the same—namely, standard normal.
itself. Using form (5.1.2.4), the reference distribution will always be the same—namely, standard normal. 139.8.
139.8.

![\begin{aligned} & P[\text { a standard normal variable } \leq-2.5] \\ & \quad+P[\text { a standard normal variable } \geq 2.5] \\ & \quad=P[\mid \text { a standard normal variable } \mid \geq 2.5] \\ & \quad=.01 \end{aligned} \begin{aligned} & P[\text { a standard normal variable } \leq-2.5] \\ & \quad+P[\text { a standard normal variable } \geq 2.5] \\ & \quad=P[\mid \text { a standard normal variable } \mid \geq 2.5] \\ & \quad=.01 \end{aligned}](https://atu0g9ctah.execute-api.ca-central-1.amazonaws.com/latest/latex?latex=%5Cbegin%7Baligned%7D%20%26%20P%5B%5Ctext%20%7B%20a%20standard%20normal%20variable%20%7D%20%5Cleq-2.5%5D%20%5C%5C%20%26%20%5Cquad%2BP%5B%5Ctext%20%7B%20a%20standard%20normal%20variable%20%7D%20%5Cgeq%202.5%5D%20%5C%5C%20%26%20%5Cquad%3DP%5B%5Cmid%20%5Ctext%20%7B%20a%20standard%20normal%20variable%20%7D%20%5Cmid%20%5Cgeq%202.5%5D%20%5C%5C%20%26%20%5Cquad%3D.01%20%5Cend%7Baligned%7D&fg=000000&font=TeX&svg=1)




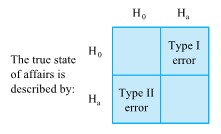
 is called the power of the significance test.
is called the power of the significance test.
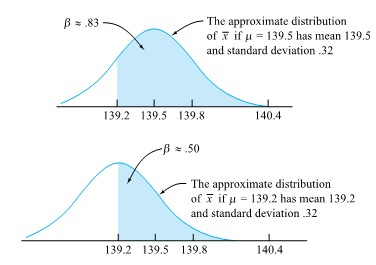

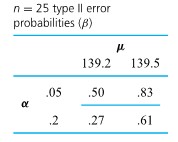
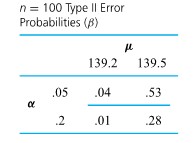







 distribution.
distribution.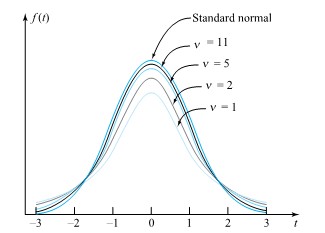
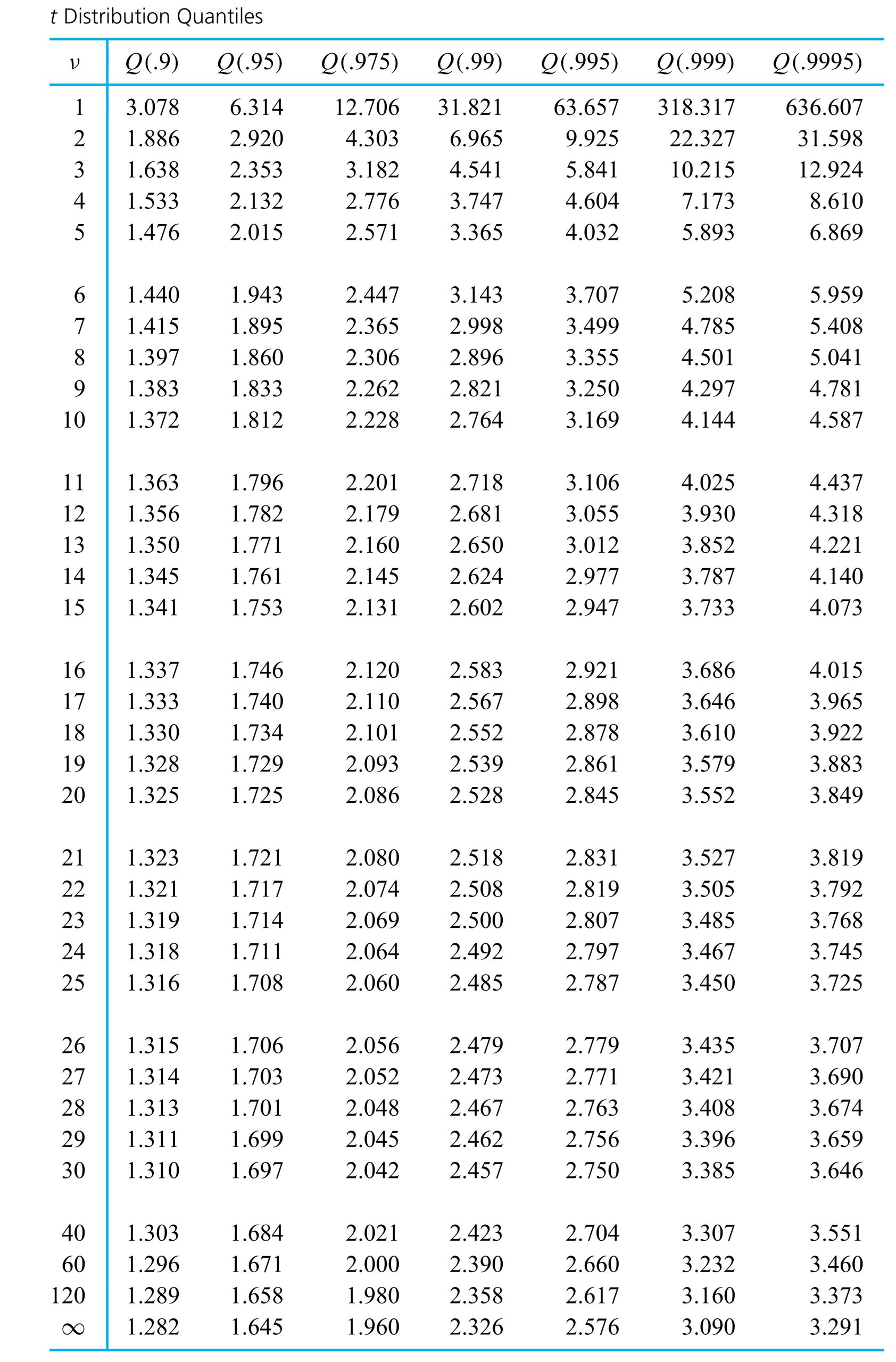
 exists. Instead, it is common to use tables (or statistical software) to evaluate common t distribution quantiles and to get at least crude bounds on the types of probabilities needed in significance testing. Table A1.2 in the Appendix 1 of statistical tables is a typical table of t quantiles. Across the top of the table are several cumulative probabilities. Down the left side are values of the degrees of freedom parameter,
exists. Instead, it is common to use tables (or statistical software) to evaluate common t distribution quantiles and to get at least crude bounds on the types of probabilities needed in significance testing. Table A1.2 in the Appendix 1 of statistical tables is a typical table of t quantiles. Across the top of the table are several cumulative probabilities. Down the left side are values of the degrees of freedom parameter, ![P[T<-1.9]=P[T>1.9]=1-P[T \leq 1.9] P[T<-1.9]=P[T>1.9]=1-P[T \leq 1.9]](https://atu0g9ctah.execute-api.ca-central-1.amazonaws.com/latest/latex?latex=P%5BT%3C-1.9%5D%3DP%5BT%3E1.9%5D%3D1-P%5BT%20%5Cleq%201.9%5D&fg=000000&font=TeX&svg=1)
 distribution. That is,
distribution. That is,![P[T \leq 1.9] \leq .95 P[T \leq 1.9] \leq .95](https://atu0g9ctah.execute-api.ca-central-1.amazonaws.com/latest/latex?latex=P%5BT%20%5Cleq%201.9%5D%20%5Cleq%20.95&fg=000000&font=TeX&svg=1)
![P[T<-1.9]<.10 P[T<-1.9]<.10](https://atu0g9ctah.execute-api.ca-central-1.amazonaws.com/latest/latex?latex=P%5BT%3C-1.9%5D%3C.10&fg=000000&font=TeX&svg=1)
![P[T \leq 2.3]<.975 P[T \leq 2.3]<.975](https://atu0g9ctah.execute-api.ca-central-1.amazonaws.com/latest/latex?latex=P%5BT%20%5Cleq%202.3%5D%3C.975&fg=000000&font=TeX&svg=1)


 random variable, we are in a position to work in exact analogy to what was done in Part 5 to find methods for confidence interval estimation and significance testing. That is, if a data-generating mechanism can be thought of as essentially equivalent to drawing independent observations from a single normal distribution, a two-sided confidence interval for µ has endpoints
random variable, we are in a position to work in exact analogy to what was done in Part 5 to find methods for confidence interval estimation and significance testing. That is, if a data-generating mechanism can be thought of as essentially equivalent to drawing independent observations from a single normal distribution, a two-sided confidence interval for µ has endpoints


 stress?” Since only n = 10 observations are available, the large-sample method of Part 5.1 is not applicable. Instead, only the method indicated by expression (5.2.1.5) is a possible option. For it to be appropriate, lifetimes must be normally distributed.
stress?” Since only n = 10 observations are available, the large-sample method of Part 5.1 is not applicable. Instead, only the method indicated by expression (5.2.1.5) is a possible option. For it to be appropriate, lifetimes must be normally distributed.
 distribution and chooses t > 0 such that
distribution and chooses t > 0 such that


 and
and  stand for underlying distributional means corresponding to the first and second conditions and
stand for underlying distributional means corresponding to the first and second conditions and  and
and  stand for corresponding sample means. Now if the two data-generating mechanisms are conceptually essentially equivalent to sampling with replacement from two distributions, Part 4 says that
stand for corresponding sample means. Now if the two data-generating mechanisms are conceptually essentially equivalent to sampling with replacement from two distributions, Part 4 says that  and
and  . The difference in sample means
. The difference in sample means 

 and
and  are large (so that
are large (so that 
 and
and  . Happily, for large
. Happily, for large 


 = 8.34 g,
= 8.34 g,  = 9.31 g, the five-step testing format produces the following summary:
= 9.31 g, the five-step testing format produces the following summary:









 and
and  ,the pooled sample variance,
,the pooled sample variance, 
 , is the square root of
, is the square root of 





 distribution assigns to the interval between −t and t corresponds to the desired confidence. And under the same conditions,
distribution assigns to the interval between −t and t corresponds to the desired confidence. And under the same conditions,
 mm^2 stress level condition 1 and the 950 N/
mm^2 stress level condition 1 and the 950 N/


 distribution is in order. Endpoints of the confidence interval for
distribution is in order. Endpoints of the confidence interval for 



 is such that the
is such that the  degrees of freedom assigns that probability to the interval between
degrees of freedom assigns that probability to the interval between  and
and 

 distribution is 2.145. So the 95% limits (5.3.3.8) for the (850 N/
distribution is 2.145. So the 95% limits (5.3.3.8) for the (850 N/ −
−  )are
)are


 distribution with numerator and denominator degrees of freedom parameters
distribution with numerator and denominator degrees of freedom parameters  and
and  is a continuous probability distribution with probability density
is a continuous probability distribution with probability density
 distribution.
distribution. (the numerator degrees of freedom) and
(the numerator degrees of freedom) and  (the denominator degrees of freedom). The values of
(the denominator degrees of freedom). The values of  and
and  quantiles, quantiles for small
quantiles, quantiles for small  stand for the
stand for the  stand for the quantile function for the
stand for the quantile function for the 

 random variable. Consider finding the .95 and .01 quantiles of
random variable. Consider finding the .95 and .01 quantiles of  4.0] and
4.0] and ![P[V<.3] P[V<.3]](https://atu0g9ctah.execute-api.ca-central-1.amazonaws.com/latest/latex?latex=P%5BV%3C.3%5D&fg=000000&font=TeX&svg=1) .
. table of quantiles, in the
table of quantiles, in the  column and
column and  row, produces the number 5.41. That is,
row, produces the number 5.41. That is,  , or (equivalently)
, or (equivalently) ![P[V<5.41]=.95 P[V<5.41]=.95](https://atu0g9ctah.execute-api.ca-central-1.amazonaws.com/latest/latex?latex=P%5BV%3C5.41%5D%3D.95&fg=000000&font=TeX&svg=1) .
. quantile of the
quantile of the 
 column and
column and  row of the table of
row of the table of  quantiles, one has
quantiles, one has
![P[V>4.0] P[V>4.0]](https://atu0g9ctah.execute-api.ca-central-1.amazonaws.com/latest/latex?latex=P%5BV%3E4.0%5D&fg=000000&font=TeX&svg=1) , one finds (using the [/latex]v_{1}=3[/latex] columns and
, one finds (using the [/latex]v_{1}=3[/latex] columns and  ), in the
), in the  distribution and then make use of expression (5.2.4.2). Using the
distribution and then make use of expression (5.2.4.2). Using the  and
and  of those underlying distributions. That is, when
of those underlying distributions. That is, when  and
and ![s_{2}^{2}[latex] come from independent samples from normal distributions, the variable <blockquote> <p style="text-align: left"><strong>5.2.4.3 </strong> [latex]F=\frac{s_{1}^{2}}{\sigma_{1}^{2}} \cdot \frac{\sigma_{2}^{2}}{s_{2}^{2}} s_{2}^{2}[latex] come from independent samples from normal distributions, the variable <blockquote> <p style="text-align: left"><strong>5.2.4.3 </strong> [latex]F=\frac{s_{1}^{2}}{\sigma_{1}^{2}} \cdot \frac{\sigma_{2}^{2}}{s_{2}^{2}}](https://atu0g9ctah.execute-api.ca-central-1.amazonaws.com/latest/latex?latex=s_%7B2%7D%5E%7B2%7D%5Blatex%5D%20come%20from%20independent%20samples%20from%20normal%20distributions%2C%20the%20variable%20%20%3Cblockquote%3E%20%20%3Cp%20style%3D%22text-align%3A%20left%22%3E%3Cstrong%3E5.2.4.3%C2%A0%20%C2%A0%20%C2%A0%20%C2%A0%20%C2%A0%20%C2%A0%20%C2%A0%20%C2%A0%20%C2%A0%20%C2%A0%3C%2Fstrong%3E%20%5Blatex%5DF%3D%5Cfrac%7Bs_%7B1%7D%5E%7B2%7D%7D%7B%5Csigma_%7B1%7D%5E%7B2%7D%7D%20%5Ccdot%20%5Cfrac%7B%5Csigma_%7B2%7D%5E%7B2%7D%7D%7Bs_%7B2%7D%5E%7B2%7D%7D&fg=000000&font=TeX&svg=1)
 distribution. (
distribution. (  associated degrees of freedom and is in the numerator of this expression, while
associated degrees of freedom and is in the numerator of this expression, while  has
has  associated degrees of freedom and is in the denominator, providing motivation for the language introduced in Definition 5.2.4.1)
associated degrees of freedom and is in the denominator, providing motivation for the language introduced in Definition 5.2.4.1) . For example, it is possible to pick appropriate F quantiles L and U such that the probability that the variable (5.2.4.3) falls between L and U corresponds to a desired confidence level. (Typically, L and U are chosen to "split the 'unconfidence' " between the upper and lower
. For example, it is possible to pick appropriate F quantiles L and U such that the probability that the variable (5.2.4.3) falls between L and U corresponds to a desired confidence level. (Typically, L and U are chosen to "split the 'unconfidence' " between the upper and lower  <U
<U



 in displays (5.2.4.5) and (5.2.4.6), so that the null hypothesis is one of equality of variances, is the only one commonly used in practice.)
in displays (5.2.4.5) and (5.2.4.6), so that the null hypothesis is one of equality of variances, is the only one commonly used in practice.)
 < # and
< # and  are (respectively) the left and right
are (respectively) the left and right  , the standard convention is to report twice the
, the standard convention is to report twice the  if
if  and to report twice the
and to report twice the  carbon steel. Part of their data are given in Table 5.2.4.1, where Rockwell hardness measurements for ten specimens from a lot of heat-treated steel specimens and five specimens from a lot of cold-rolled steel specimens are represented.
carbon steel. Part of their data are given in Table 5.2.4.1, where Rockwell hardness measurements for ten specimens from a lot of heat-treated steel specimens and five specimens from a lot of cold-rolled steel specimens are represented.


 and
and  , and a five-step significance test of equality of variances based on the variable (5.2.4.6) proceeds as follows:
, and a five-step significance test of equality of variances based on the variable (5.2.4.6) proceeds as follows:![]\mathrm{H}_{0}: \frac{\sigma_{1}^{2}}{\sigma_{2}^{2}}=1 ]\mathrm{H}_{0}: \frac{\sigma_{1}^{2}}{\sigma_{2}^{2}}=1](https://atu0g9ctah.execute-api.ca-central-1.amazonaws.com/latest/latex?latex=%5D%5Cmathrm%7BH%7D_%7B0%7D%3A%20%5Cfrac%7B%5Csigma_%7B1%7D%5E%7B2%7D%7D%7B%5Csigma_%7B2%7D%5E%7B2%7D%7D%3D1&fg=000000&font=TeX&svg=1)


 distribution, and both large observed f and small observed f will constitute evidence against
distribution, and both large observed f and small observed f will constitute evidence against  .
.
![2 P\left[\text { an } F_{9,4} \text { random variable } \geq 4.6\right] 2 P\left[\text { an } F_{9,4} \text { random variable } \geq 4.6\right]](https://atu0g9ctah.execute-api.ca-central-1.amazonaws.com/latest/latex?latex=2%20P%5Cleft%5B%5Ctext%20%7B%20an%20%7D%20F_%7B9%2C4%7D%20%5Ctext%20%7B%20random%20variable%20%7D%20%5Cgeq%204.6%5Cright%5D&fg=000000&font=TeX&svg=1)
 . Now the .95 quantile of the
. Now the .95 quantile of the  distribution is 3.63, implying that the .05 quantile of the
distribution is 3.63, implying that the .05 quantile of the  . Thus, a 90 % confidence interval for the ratio of standard deviations
. Thus, a 90 % confidence interval for the ratio of standard deviations 
 /
/ to be on the order of 1.5 and predicted a period of two years or less for the recovery of the capital improvement cost of equipping all the company’s ream cutters with automatic brakes.
to be on the order of 1.5 and predicted a period of two years or less for the recovery of the capital improvement cost of equipping all the company’s ream cutters with automatic brakes.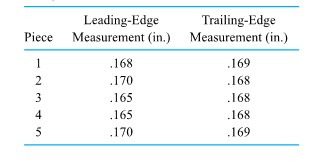
 , if n (the number of data pairs) is large, endpoints of a confidence interval for the underlying mean difference,
, if n (the number of data pairs) is large, endpoints of a confidence interval for the underlying mean difference,  , are
, are
 is the sample standard deviation of d1 , d2 ,…,
is the sample standard deviation of d1 , d2 ,…,



 =−.0008 in. and
=−.0008 in. and  = .0023 in. So, first investigating the plausibility of a “no consistent difference” hypothesis in a five-step significance testing format, gives the following:
= .0023 in. So, first investigating the plausibility of a “no consistent difference” hypothesis in a five-step significance testing format, gives the following:

 random variable|≥.78], which can be seen from Table A1.2 to be larger than 2(.10) = .2. The data in hand are not convincing in favor of a systematic difference between leading- and trailing-edge measurements.
random variable|≥.78], which can be seen from Table A1.2 to be larger than 2(.10) = .2. The data in hand are not convincing in favor of a systematic difference between leading- and trailing-edge measurements.
 =−.0008, is just a result of sampling variability.
=−.0008, is just a result of sampling variability.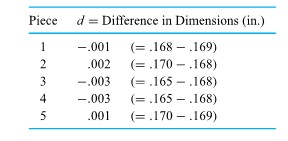
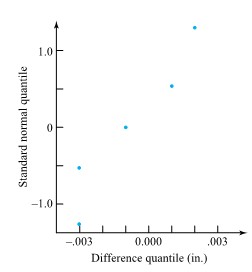
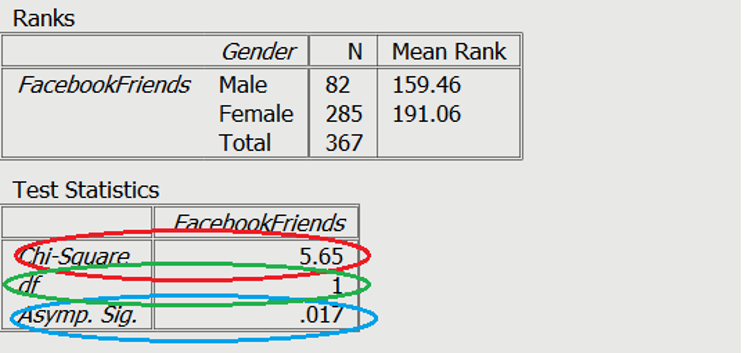
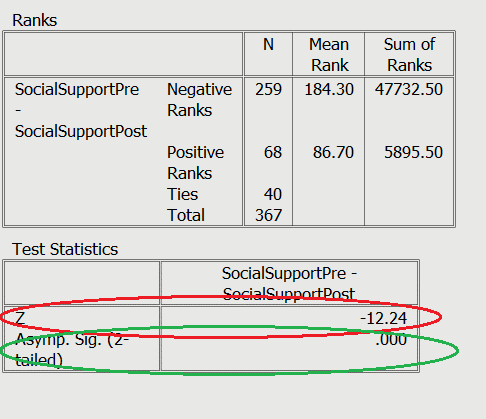
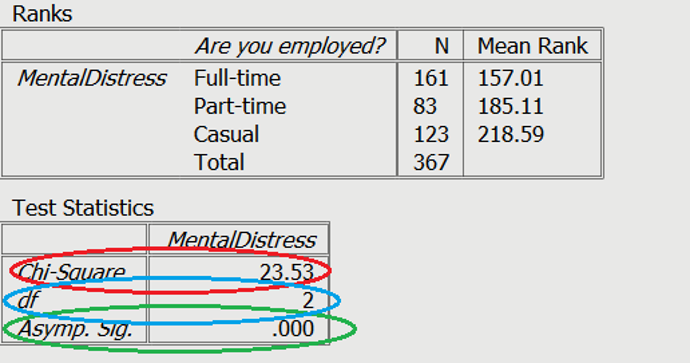

 amounts to making a scatterplot of compressive strength versus formula number. Such a plot is shown in Figure 6.1.1.1. The general message conveyed by Figure 6.1.1.1 is that there are clear differences in mean compressive strengths between the formulas but that the variabilities in compressive strengths are roughly comparable for the eight different formulas.
amounts to making a scatterplot of compressive strength versus formula number. Such a plot is shown in Figure 6.1.1.1. The general message conveyed by Figure 6.1.1.1 is that there are clear differences in mean compressive strengths between the formulas but that the variabilities in compressive strengths are roughly comparable for the eight different formulas.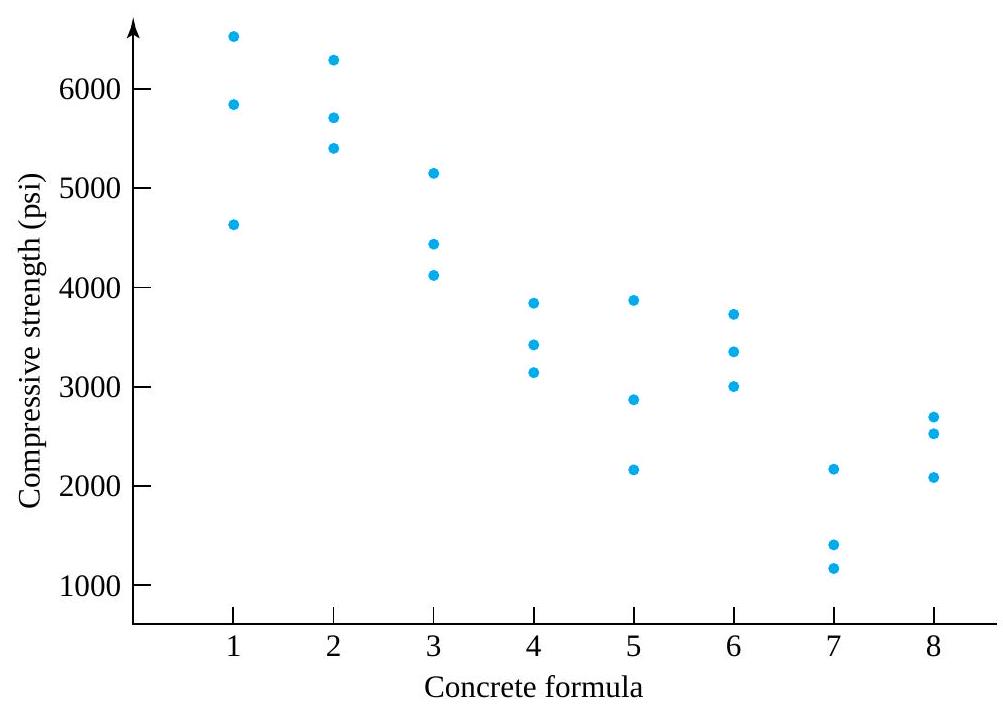
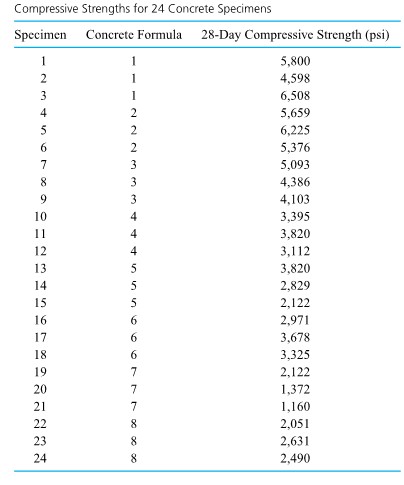
 springs of type 1 (a 4 in. design with a theoretical spring constant of 1.86),
springs of type 1 (a 4 in. design with a theoretical spring constant of 1.86),  springs of type 2 (a 6 in. design with a theoretical spring constant of 2.63), and
springs of type 2 (a 6 in. design with a theoretical spring constant of 2.63), and  springs of type 3 (a 4 in. design with a theoretical spring constant of 2.12), using an
springs of type 3 (a 4 in. design with a theoretical spring constant of 2.12), using an  load. The students’ experimental values are given in Table 6.1.1.2
load. The students’ experimental values are given in Table 6.1.1.2 . spring types but that no such difference between the two 4 in. spring types is obvious. Of course, the information in Table 6.1.1.2 could also be presented in side-by-side dot diagram form, as in Figure 6.1.1.3.
. spring types but that no such difference between the two 4 in. spring types is obvious. Of course, the information in Table 6.1.1.2 could also be presented in side-by-side dot diagram form, as in Figure 6.1.1.3.
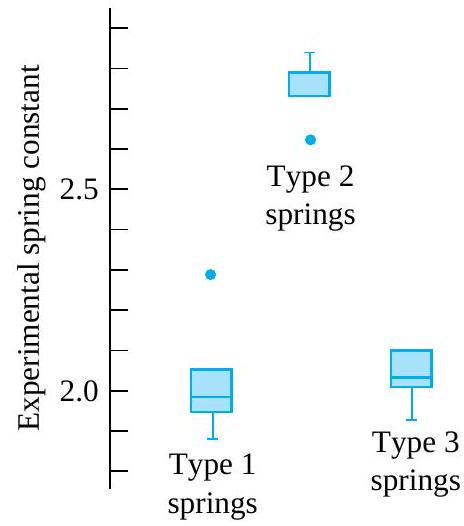
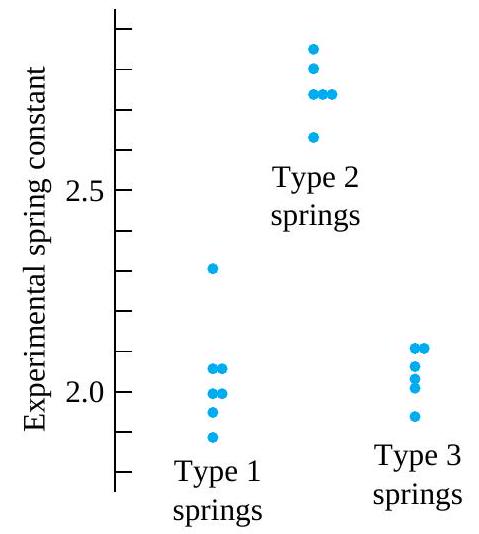
 samples of respective sizes
samples of respective sizes  are independent samples from normal underlying distributions with a common variance-say,
are independent samples from normal underlying distributions with a common variance-say,  version of this one-way (as opposed, for example, to several-way factorial) model led to useful inference methods for
version of this one-way (as opposed, for example, to several-way factorial) model led to useful inference methods for  , this general version will support a variety of useful inference methods for
, this general version will support a variety of useful inference methods for 


 is the
is the  ,
,  are independent normal random variables with mean 0 and variance
are independent normal random variables with mean 0 and variance  and the variance
and the variance 







 deterministic response + noise
deterministic response + noise  are meant to approximate the deterministic part of a system response
are meant to approximate the deterministic part of a system response  , and
, and are therefore meant to approximate the corresponding noise in the response
are therefore meant to approximate the corresponding noise in the response  .
. in equation (6.1.2.1) are assumed to be iid normal
in equation (6.1.2.1) are assumed to be iid normal  random variables then suggests that the
random variables then suggests that the  ought to look at least approximately like a random sample from a normal distribution.
ought to look at least approximately like a random sample from a normal distribution. is more than three times the size of
is more than three times the size of  . But the sample sizes here are so small that a largest ratio of sample standard deviations on the order of 3.2 is hardly unusual (for
. But the sample sizes here are so small that a largest ratio of sample standard deviations on the order of 3.2 is hardly unusual (for  samples of size 3 from a normal distribution). Note from the
samples of size 3 from a normal distribution). Note from the  would yield a
would yield a  residuals. Some of the calculations necessary to compute residuals for the data in Table 6.1.1.1 (using the fitted values appearing as sample means in Table 6.1.2.1) are shown in Table 6.1.2.2. Figures 6.1.2.2 and 6.1.2.3 are, respectively, a plot of residuals versus fitted
residuals. Some of the calculations necessary to compute residuals for the data in Table 6.1.1.1 (using the fitted values appearing as sample means in Table 6.1.2.1) are shown in Table 6.1.2.2. Figures 6.1.2.2 and 6.1.2.3 are, respectively, a plot of residuals versus fitted  versus
versus  ) and a normal plot of all 24 residuals.
) and a normal plot of all 24 residuals.

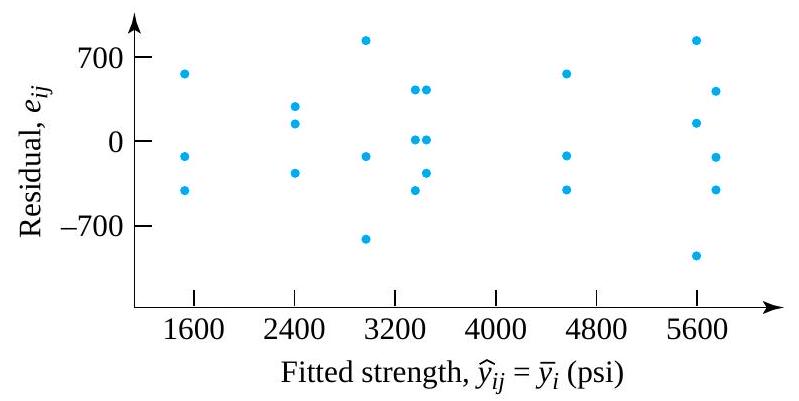
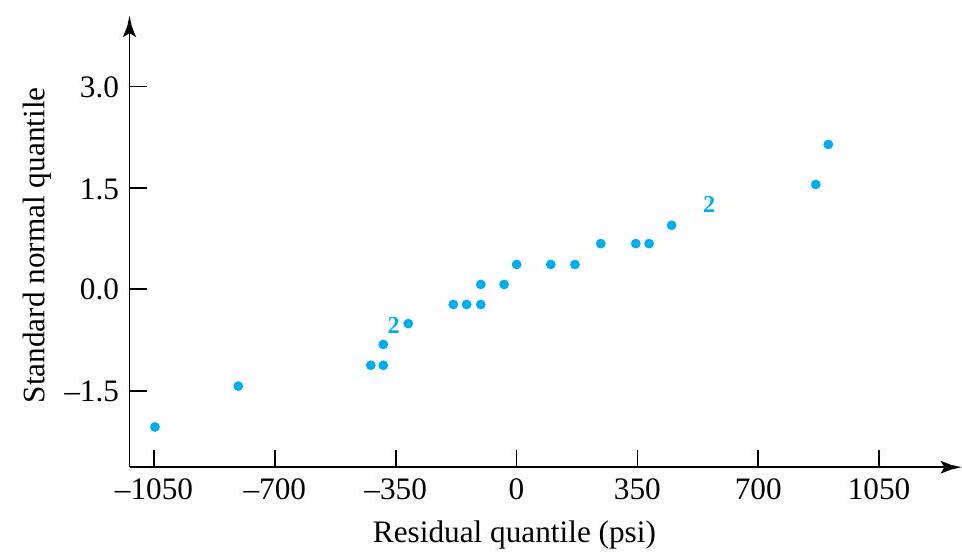
 is not a compelling reason to abandon a one-way model description of the spring constants. (A look at the
is not a compelling reason to abandon a one-way model description of the spring constants. (A look at the  and
and  distribution .9 and .95 quantiles. So even if there were only two rather than three samples involved, a variance ratio of 4.38 would yield a
distribution .9 and .95 quantiles. So even if there were only two rather than three samples involved, a variance ratio of 4.38 would yield a  are large enough that it makes sense to look at sample-by-sample normal plots of the spring constant data. Such plots, drawn on the same set of axes, are shown in Figure 6.1.2.4. Further, use of the fitted values
are large enough that it makes sense to look at sample-by-sample normal plots of the spring constant data. Such plots, drawn on the same set of axes, are shown in Figure 6.1.2.4. Further, use of the fitted values  listed in Table 6.1.2.3 with the original data given in Table 6.1.1.2 produces 19 residuals, as partially illustrated in Table 6.1.2.4. Then Figures 6.1.2.5 and 6.1.2.6, respectively, show a plot of residuals versus fitted responses and a normal plot of all 19 residuals.
listed in Table 6.1.2.3 with the original data given in Table 6.1.1.2 produces 19 residuals, as partially illustrated in Table 6.1.2.4. Then Figures 6.1.2.5 and 6.1.2.6, respectively, show a plot of residuals versus fitted responses and a normal plot of all 19 residuals.

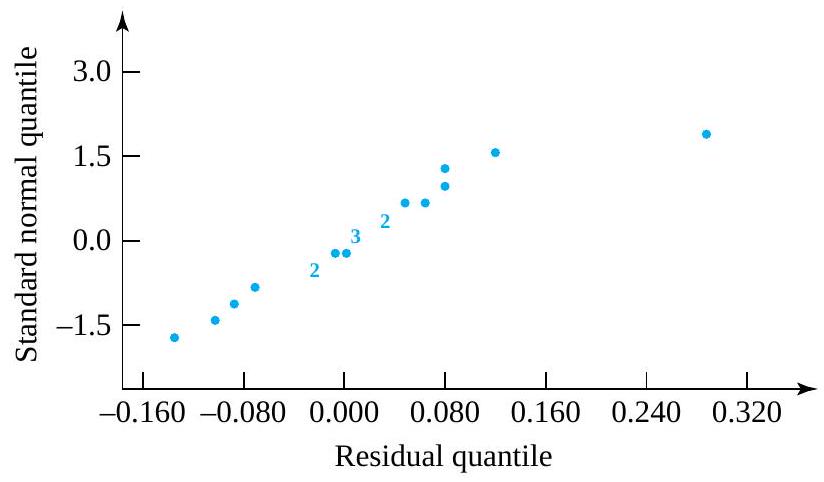
 . Similar to what was done in the
. Similar to what was done in the  , the pooled sample variance,
, the pooled sample variance,  , is the weighted average of the sample variances, where the weights are the sample sizes minus 1 . That is,
, is the weighted average of the sample variances, where the weights are the sample sizes minus 1 . That is,
 , is the square root of
, is the square root of  .
. based on two samples,
based on two samples,  and is a mathematically convenient form of compromise value.
and is a mathematically convenient form of compromise value.




 .
. are 3 , and
are 3 , and ![\begin{aligned} s_{\mathrm{P}}^{2} & =\frac{(3-1)(965.6)^{2}+(3-1)(432.3)^{2}+\cdots+(3-1)(302.5)^{2}}{(3-1)+(3-1)+\cdots+(3-1)} \\ & =\frac{2\left[(965.6)^{2}+(432.3)^{2}+\cdots+(302.5)^{2}\right]}{16} \\ & =\frac{2,705,705}{8} \\ & =338,213(\mathrm{psi})^{2} \end{aligned} \begin{aligned} s_{\mathrm{P}}^{2} & =\frac{(3-1)(965.6)^{2}+(3-1)(432.3)^{2}+\cdots+(3-1)(302.5)^{2}}{(3-1)+(3-1)+\cdots+(3-1)} \\ & =\frac{2\left[(965.6)^{2}+(432.3)^{2}+\cdots+(302.5)^{2}\right]}{16} \\ & =\frac{2,705,705}{8} \\ & =338,213(\mathrm{psi})^{2} \end{aligned}](https://atu0g9ctah.execute-api.ca-central-1.amazonaws.com/latest/latex?latex=%5Cbegin%7Baligned%7D%20s_%7B%5Cmathrm%7BP%7D%7D%5E%7B2%7D%20%26%20%3D%5Cfrac%7B%283-1%29%28965.6%29%5E%7B2%7D%2B%283-1%29%28432.3%29%5E%7B2%7D%2B%5Ccdots%2B%283-1%29%28302.5%29%5E%7B2%7D%7D%7B%283-1%29%2B%283-1%29%2B%5Ccdots%2B%283-1%29%7D%20%5C%5C%C2%A0%26%20%3D%5Cfrac%7B2%5Cleft%5B%28965.6%29%5E%7B2%7D%2B%28432.3%29%5E%7B2%7D%2B%5Ccdots%2B%28302.5%29%5E%7B2%7D%5Cright%5D%7D%7B16%7D%20%5C%5C%C2%A0%26%20%3D%5Cfrac%7B2%2C705%2C705%7D%7B8%7D%20%5C%5C%C2%A0%26%20%3D338%2C213%28%5Cmathrm%7Bpsi%7D%29%5E%7B2%7D%C2%A0%5Cend%7Baligned%7D&fg=000000&font=TeX&svg=1)



 distribution. Thus, in a manner exactly parallel to the derivation in Part 5, a two-sided confidence interval for
distribution. Thus, in a manner exactly parallel to the derivation in Part 5, a two-sided confidence interval for ![\sigma^{2}[latex] has endpoints</div> <div style="text-align: left">.</div> <blockquote> <div style="text-align: left"><strong>6.1.3.4 </strong>[latex]\frac{(n-r) s_{\mathrm{P}}^{2}}{U} \text { and } \frac{(n-r) s_{\mathrm{P}}^{2}}{L} \sigma^{2}[latex] has endpoints</div> <div style="text-align: left">.</div> <blockquote> <div style="text-align: left"><strong>6.1.3.4 </strong>[latex]\frac{(n-r) s_{\mathrm{P}}^{2}}{U} \text { and } \frac{(n-r) s_{\mathrm{P}}^{2}}{L}](https://atu0g9ctah.execute-api.ca-central-1.amazonaws.com/latest/latex?latex=%5Csigma%5E%7B2%7D%5Blatex%5D%20has%20endpoints%3C%2Fdiv%3E%20%3Cdiv%20style%3D%22text-align%3A%20left%22%3E.%3C%2Fdiv%3E%20%3Cblockquote%3E%20%3Cdiv%20style%3D%22text-align%3A%20left%22%3E%3Cstrong%3E6.1.3.4%C2%A0%20%C2%A0%20%C2%A0%20%C2%A0%20%C2%A0%20%3C%2Fstrong%3E%5Blatex%5D%5Cfrac%7B%28n-r%29%20s_%7B%5Cmathrm%7BP%7D%7D%5E%7B2%7D%7D%7BU%7D%20%5Ctext%20%7B%20and%20%7D%20%5Cfrac%7B%28n-r%29%20s_%7B%5Cmathrm%7BP%7D%7D%5E%7B2%7D%7D%7BL%7D&fg=000000&font=TeX&svg=1)
 and
and  is the desired confidence level. And, of course, a one-sided interval is available by using only one of the endpoints (6.1.3.4) and choosing
is the desired confidence level. And, of course, a one-sided interval is available by using only one of the endpoints (6.1.3.4) and choosing  is the desired confidence.
is the desired confidence. confidence interval for
confidence interval for  degrees of freedom are associated with
degrees of freedom are associated with  distribution. These are 7.962 and 26.296, respectively. Thus a confidence interval for
distribution. These are 7.962 and 26.296, respectively. Thus a confidence interval for 



 distribution. Hence, a two-sided confidence interval for the
distribution. Hence, a two-sided confidence interval for the 
 to
to  to
to  , the variable
, the variable
 has endpoints
has endpoints
 .
. (for
(for  ). The virtues of formulas (6.2.1.1) and (6.2.1.2) (in comparison to the corresponding formulas from Part 5) are that (when appropriate) for a given confidence, they will tend to produce shorter intervals than their Part 5 counterparts.
). The virtues of formulas (6.2.1.1) and (6.2.1.2) (in comparison to the corresponding formulas from Part 5) are that (when appropriate) for a given confidence, they will tend to produce shorter intervals than their Part 5 counterparts. and
and  . So the .95 quantile of the
. So the .95 quantile of the  distribution, namely 1.746, is appropriate for use in both formulas (6.2.1.1) and (6.2.1.2).
distribution, namely 1.746, is appropriate for use in both formulas (6.2.1.1) and (6.2.1.2). is 3 , the plus-or-minus part of formula (6.2.1.1) gives
is 3 , the plus-or-minus part of formula (6.2.1.1) gives
 psi precision could be attached to any one of the sample means in Table 6.2.1.1 as an estimate of the corresponding formula’s mean strength. For example, since
psi precision could be attached to any one of the sample means in Table 6.2.1.1 as an estimate of the corresponding formula’s mean strength. For example, since  psi, a
psi, a  has endpoints
has endpoints


 psi precision could be attached to any difference between sample means in Table 6.2.1.1 as an estimate of the corresponding difference in formula mean strengths. For instance, since
psi precision could be attached to any difference between sample means in Table 6.2.1.1 as an estimate of the corresponding difference in formula mean strengths. For instance, since  , a
, a  has endpoints
has endpoints

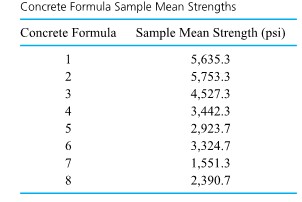
 and
and  reflects the reduction in uncertainty associated with
reflects the reduction in uncertainty associated with 
 confidence intervals have associated confidences
confidence intervals have associated confidences  , the Bonferroni inequality says that the simultaneous or joint confidence that all
, the Bonferroni inequality says that the simultaneous or joint confidence that all  ) satisfies
) satisfies
 is no larger than the sum of the
is no larger than the sum of the  confidence levels have a joint or simultaneous confidence level of at least 95%.)
confidence levels have a joint or simultaneous confidence level of at least 95%.) pairs of mean responses
pairs of mean responses  . Section 6.2 argued thata single difference in mean responses,
. Section 6.2 argued thata single difference in mean responses,  versus
versus  versus
versus  versus
versus  versus
versus  , and
, and  versus
versus  ). If one wishes to guarantee a reasonable simultaneous confidence level for all these comparisons via the crude Bonferroni idea, a huge individual confidence level is required for the intervals (6.2.3.1). For example, the Bonferroni inequality requires
). If one wishes to guarantee a reasonable simultaneous confidence level for all these comparisons via the crude Bonferroni idea, a huge individual confidence level is required for the intervals (6.2.3.1). For example, the Bonferroni inequality requires  individual confidence for 28 intervals in order to guarantee simultaneous
individual confidence for 28 intervals in order to guarantee simultaneous  confidence.
confidence. such that the set of two-sided intervals with endpoints
such that the set of two-sided intervals with endpoints
 ) is read from Table A5A or
) is read from Table A5A or  .99) is read from Table A5B) in the estimation of all differences
.99) is read from Table A5B) in the estimation of all differences  ).
).



 row of Table A5A.)
row of Table A5A.)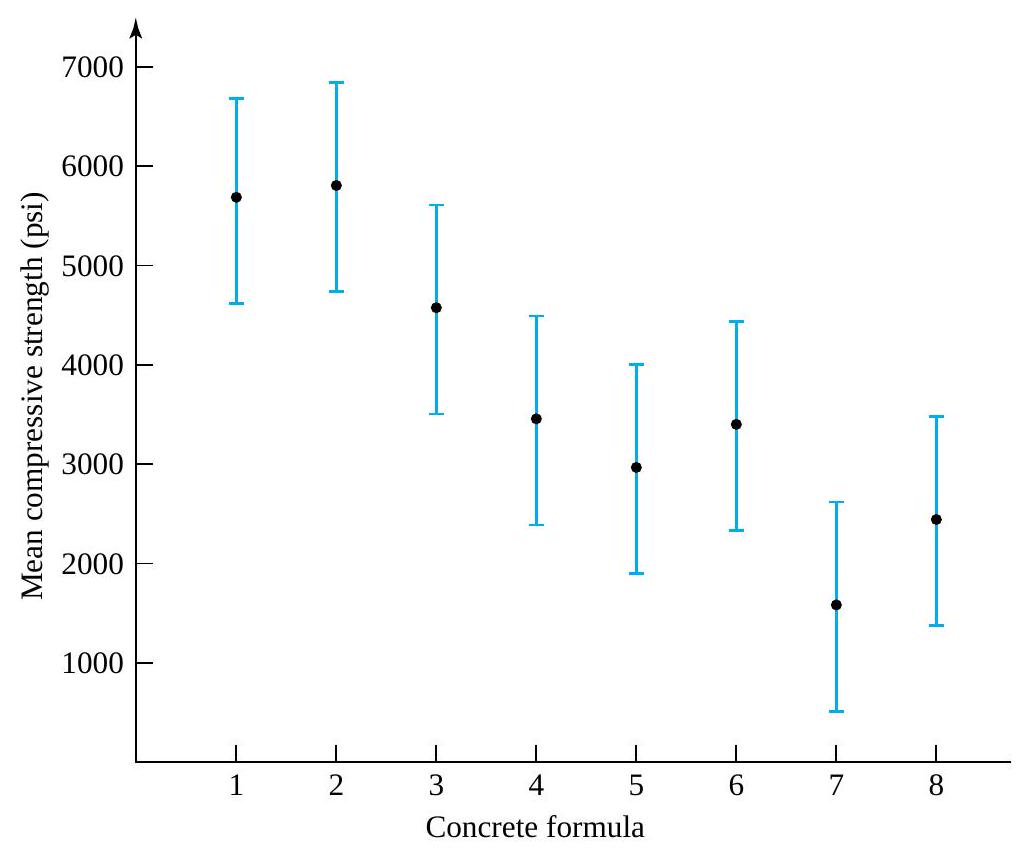






 and \#.
and \#.



 , the number of observations in hand ignoring the fact that
, the number of observations in hand ignoring the fact that  for the grand sample average of response
for the grand sample average of response 
 but is a weighted average of the sample means
but is a weighted average of the sample means  . On the other hand,
. On the other hand,  , and
, and  ,
,

 is a natural estimate of the common mean. (All underlying distributions are the same, so the data in hand are reasonably thought of not as
is a natural estimate of the common mean. (All underlying distributions are the same, so the data in hand are reasonably thought of not as  are indicators of possible differences among the
are indicators of possible differences among the 
 or as an unweighted sum, where there is a term in the sum for each raw data point and therefore
or as an unweighted sum, where there is a term in the sum for each raw data point and therefore  , giving
, giving
 distribution. So the hypothesis of equality of
distribution. So the hypothesis of equality of  : not
: not  and the 8 sample means
and the 8 sample means  , in this situation,
, in this situation,


 distribution. So
distribution. So![p \text {-value }=P\left[\text { an } F_{7,16} \text { random variable } \geq 20.0\right]<.001 p \text {-value }=P\left[\text { an } F_{7,16} \text { random variable } \geq 20.0\right]<.001](https://atu0g9ctah.execute-api.ca-central-1.amazonaws.com/latest/latex?latex=p%20%5Ctext%20%7B-value%20%7D%3DP%5Cleft%5B%5Ctext%20%7B%20an%20%7D%20F_%7B7%2C16%7D%20%5Ctext%20%7B%20random%20variable%20%7D%20%5Cgeq%2020.0%5Cright%5D%3C.001&fg=000000&font=TeX&svg=1)
 are not all equal.
are not all equal.




 , the sum of squared differences between the raw data values and the grand sample mean, will be called the total sum of squares and denoted as SSTot.
, the sum of squared differences between the raw data values and the grand sample mean, will be called the total sum of squares and denoted as SSTot. will be called the treatment sum of squares and denoted as SSTr.
will be called the treatment sum of squares and denoted as SSTr. (which is
(which is  in the unstructured situation) will be called the error sum of squares and denoted as SSE.
in the unstructured situation) will be called the error sum of squares and denoted as SSE.
 of
of  (corresponding to the source), degrees of freedom (corresponding to the source), Mean Square (corresponding to the source), and
(corresponding to the source), degrees of freedom (corresponding to the source), Mean Square (corresponding to the source), and  (for testing the significance of the source in contributing to the overall observed variability). The entries in the Source column of the table are shown here as being Treatments, Error, and Total. But the name Treatments is sometimes replaced by Between (Samples), and the name Error is sometimes replaced by Within (Samples) or Residual. The first two entries in the SS column must sum to the third, as indicated in equation (6.3.3.3). Similarly, the Treatments and Error degrees of freedom add to the Total degrees of freedom,
(for testing the significance of the source in contributing to the overall observed variability). The entries in the Source column of the table are shown here as being Treatments, Error, and Total. But the name Treatments is sometimes replaced by Between (Samples), and the name Error is sometimes replaced by Within (Samples) or Residual. The first two entries in the SS column must sum to the third, as indicated in equation (6.3.3.3). Similarly, the Treatments and Error degrees of freedom add to the Total degrees of freedom,  . Notice that the entries in the
. Notice that the entries in the  column are those attached to the numerator and denominator, respectively, of the test statistic in equation (6.3.2.3). The ratios of sums of squares to degrees of freedom are called mean squares, here the mean square for treatments (MSTr) and the mean square for error (MSE). Verify that in the present context,
column are those attached to the numerator and denominator, respectively, of the test statistic in equation (6.3.2.3). The ratios of sums of squares to degrees of freedom are called mean squares, here the mean square for treatments (MSTr) and the mean square for error (MSE). Verify that in the present context,  and
and  is the numerator of the
is the numerator of the 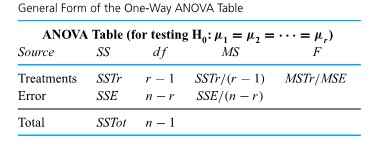

 and
and 

 .
.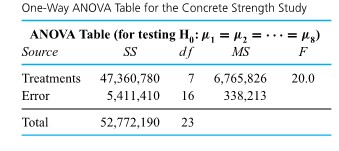
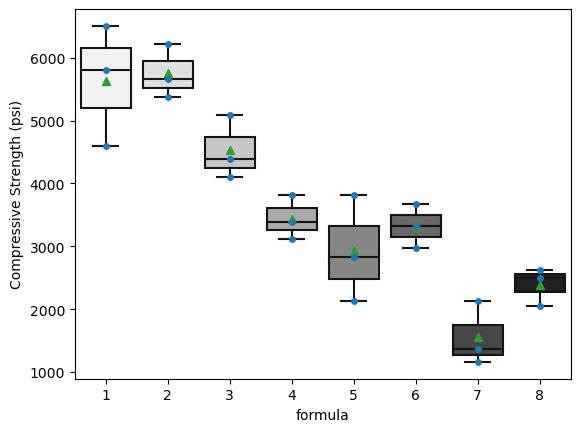
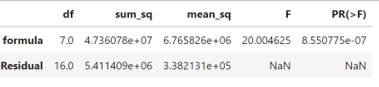
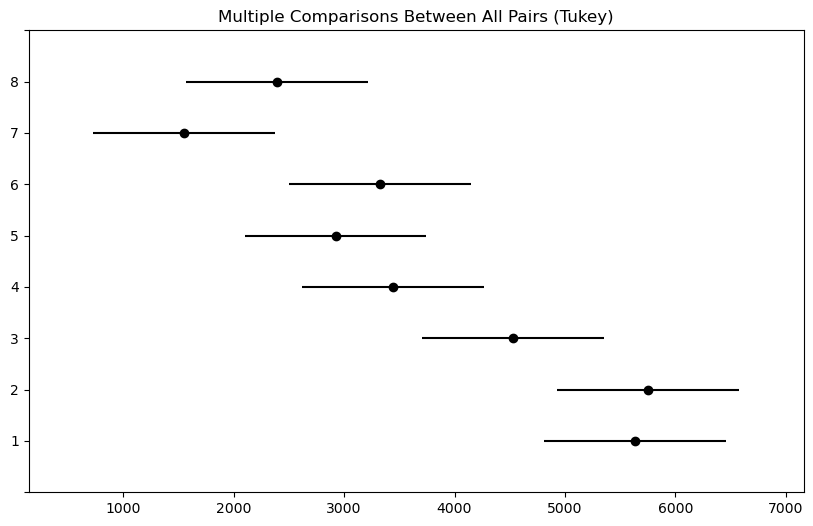

 , polyvinyl alcohol, and water was prepared, dried overnight, crushed, and sieved to obtain 100 mesh size grains. These were pressed into cylinders at pressures from 2,000 psi to 10,000 psi, and cylinder densities were calculated. Table 7.1.1.1 gives the data that were obtained, and a simple scatterplot of these data is given in Figure 7.1.1.1.
, polyvinyl alcohol, and water was prepared, dried overnight, crushed, and sieved to obtain 100 mesh size grains. These were pressed into cylinders at pressures from 2,000 psi to 10,000 psi, and cylinder densities were calculated. Table 7.1.1.1 gives the data that were obtained, and a simple scatterplot of these data is given in Figure 7.1.1.1.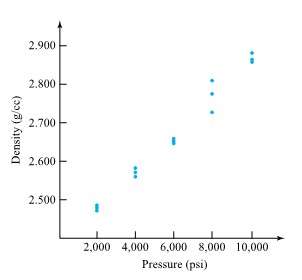


 are the observed responses and
are the observed responses and  are corresponding responses predicted or fitted by the equation.
are corresponding responses predicted or fitted by the equation.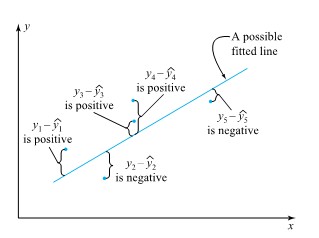

 and intercept
and intercept  is
is
 is an exercise in calculus. The partial derivatives of
is an exercise in calculus. The partial derivatives of  and
and  may be set equal to zero, and the two resulting equations may be solved simultaneously for
may be set equal to zero, and the two resulting equations may be solved simultaneously for 



 and
and .
.



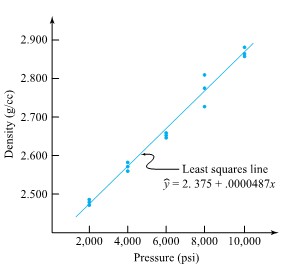



 is
is
 so that
so that 


 . Further,
. Further,  is a measure of raw variability in y, while
is a measure of raw variability in y, while  is a measure of variation in y remaining after fitting the equation. So the nonnegative difference
is a measure of variation in y remaining after fitting the equation. So the nonnegative difference  is a measure of the variability in y accounted for in the equation-fitting process.
is a measure of the variability in y accounted for in the equation-fitting process.  values for all n = 15 data points in the original data set. These are given in Table 7.1.2.1
values for all n = 15 data points in the original data set. These are given in Table 7.1.2.1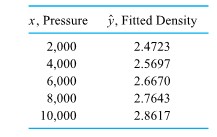

 from equation 7.1.2.2
from equation 7.1.2.2
 and the fitted values
and the fitted values  . (Since in the present situation of fitting a line, the
. (Since in the present situation of fitting a line, the  values,
values, 


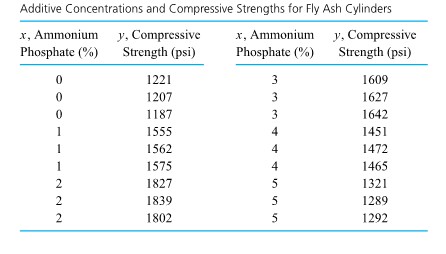

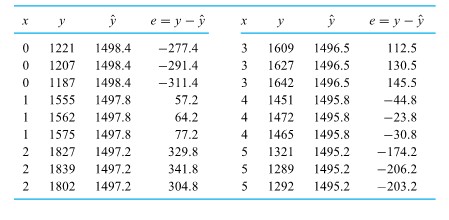
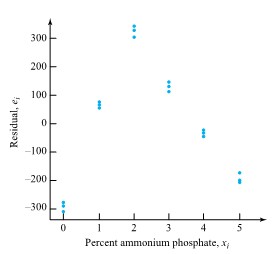

 were treated as a sample of 15 numbers and normal-plotted (using the methods we have introduced previously) to produce Figure 7.1.3.4.
were treated as a sample of 15 numbers and normal-plotted (using the methods we have introduced previously) to produce Figure 7.1.3.4.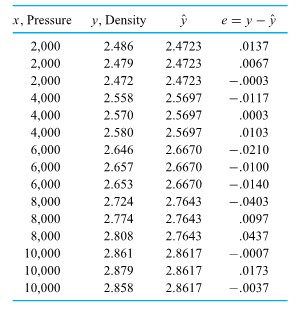
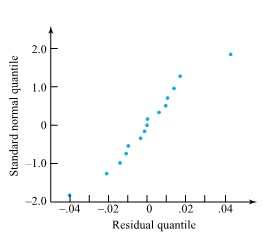

 is considered, along with inference for the average response at a given x . There follows a discussion of prediction and tolerance intervals for responses at a given setting of x . Next is an exposition of ANOVA ideas in the present situation. The section then closes with an illustration of how statistical software expedites the calculations introduced in the section.
is considered, along with inference for the average response at a given x . There follows a discussion of prediction and tolerance intervals for responses at a given setting of x . Next is an exposition of ANOVA ideas in the present situation. The section then closes with an illustration of how statistical software expedites the calculations introduced in the section. were treated as r unrestricted parameters. Turning now to the matter of inference based on data pairs
were treated as r unrestricted parameters. Turning now to the matter of inference based on data pairs 
 exhibiting an approximately linear scatterplot, one once again proceeds by imposing a restriction on the one-way model (7.2.1.1). In words, the model assumptions will be that there are underlying normal distributions for the response y with a common variance
exhibiting an approximately linear scatterplot, one once again proceeds by imposing a restriction on the one-way model (7.2.1.1). In words, the model assumptions will be that there are underlying normal distributions for the response y with a common variance  that change linearly in
that change linearly in  ,
,
 . Figure 7.2.1.1 is a pictorial representation of the “constant variance, normal, linear (in x ) mean” model.
. Figure 7.2.1.1 is a pictorial representation of the “constant variance, normal, linear (in x ) mean” model.


 ).
).
 ).
). degrees of freedom and the standard error of the line-fitting model (
degrees of freedom and the standard error of the line-fitting model ( , an estimated standard deviation of the response variable (
, an estimated standard deviation of the response variable ( ).
).

 estimates the level of basic background variation,
estimates the level of basic background variation,  (the pooled sample standard deviation) is another way of investigating the appropriateness of model 7.2.1.2. A
(the pooled sample standard deviation) is another way of investigating the appropriateness of model 7.2.1.2. A 





 and
and 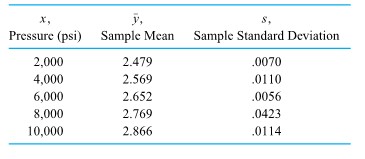


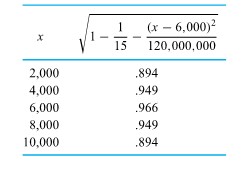
 times the appropriate entry of the second column of Table 7.2.1.3 then puts them all on equal footing, so to speak. Table 7.2.1.4 shows both the raw residuals
times the appropriate entry of the second column of Table 7.2.1.3 then puts them all on equal footing, so to speak. Table 7.2.1.4 shows both the raw residuals
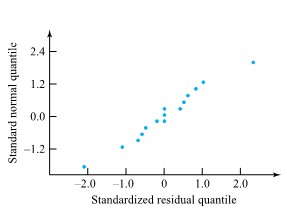




 distribution. The standard arguments of Part 5 applied to expression 7.2.2.2 then show that
distribution. The standard arguments of Part 5 applied to expression 7.2.2.2 then show that

 reference distribution. More importantly, under the simple linear re-
reference distribution. More importantly, under the simple linear re-

 distribution in formula (7.2.2.5). That is, one can use endpoints
distribution in formula (7.2.2.5). That is, one can use endpoints


 have mean responses differing by
have mean responses differing by  . One then simply multiplies endpoints of a confidence interval for
. One then simply multiplies endpoints of a confidence interval for 

 is (i.e., the more spread out the
is (i.e., the more spread out the ![[a,b] [a,b]](https://atu0g9ctah.execute-api.ca-central-1.amazonaws.com/latest/latex?latex=%5Ba%2Cb%5D&fg=000000&font=TeX&svg=1) , taking
, taking  of them at
of them at  and
and  produces the best possible precision for estimating the slope
produces the best possible precision for estimating the slope 



 term appearing as a numerator in expression (7.2.3.3), the
term appearing as a numerator in expression (7.2.3.3), the 




 distribution. A one-sided interval is made in the usual way based on one endpoint from formula (7.2.3.7).
distribution. A one-sided interval is made in the usual way based on one endpoint from formula (7.2.3.7).




 probability assigned to the interval (0,
probability assigned to the interval (0, 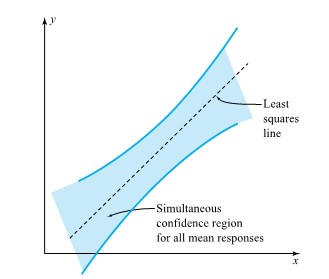
 and
and  degrees of freedom are involved in the use of formula (7.2.3.8), simultaneous limits of the form
degrees of freedom are involved in the use of formula (7.2.3.8), simultaneous limits of the form



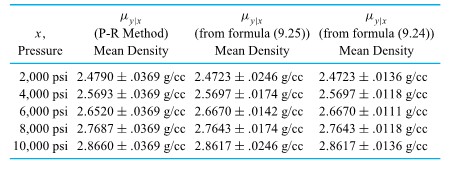
 is one additional observation, coming from the distribution of responses corresponding to a particular x ,and
is one additional observation, coming from the distribution of responses corresponding to a particular x ,and 



 is appropriately chosen (depending upon the data, p, x , and the desired confidence level).
is appropriately chosen (depending upon the data, p, x , and the desired confidence level). to
to 










 reference distribution, where large observed values of the test statistic constitute evidence against
reference distribution, where large observed values of the test statistic constitute evidence against  , which doesn’t depend on x . (Actually, a better interpretation of a test of hypothesis (7.2.5.2) is as a test of whether a linear term in x adds significantly to one’s ability to model the response y after accounting for an overall mean response.)
, which doesn’t depend on x . (Actually, a better interpretation of a test of hypothesis (7.2.5.2) is as a test of whether a linear term in x adds significantly to one’s ability to model the response y after accounting for an overall mean response.)



![[latex]\mathrm{H}_0: \beta_1=0 [latex]\mathrm{H}_0: \beta_1=0](https://atu0g9ctah.execute-api.ca-central-1.amazonaws.com/latest/latex?latex=%5Blatex%5D%5Cmathrm%7BH%7D_0%3A%20%5Cbeta_1%3D0&fg=000000&font=TeX&svg=1) [/latex] is
[/latex] is![P\left[\text { an } F_{1,13} \text { random variable }>717\right]<.001 P\left[\text { an } F_{1,13} \text { random variable }>717\right]<.001](https://atu0g9ctah.execute-api.ca-central-1.amazonaws.com/latest/latex?latex=P%5Cleft%5B%5Ctext%20%7B%20an%20%7D%20F_%7B1%2C13%7D%20%5Ctext%20%7B%20random%20variable%20%7D%3E717%5Cright%5D%3C.001&fg=000000&font=TeX&svg=1)
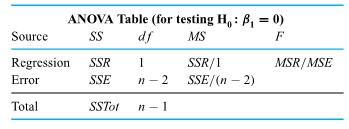
 =
=  and
and 
 data. Next comes the fitting of surfaces to data where a response
data. Next comes the fitting of surfaces to data where a response  . In both cases, the discussion will stress how useful
. In both cases, the discussion will stress how useful  and residual plotting are and will consider the question of choosing between possible fitted equations. Lastly, we include some additional practical cautions.
and residual plotting are and will consider the question of choosing between possible fitted equations. Lastly, we include some additional practical cautions.

 is conceptually only slightly more difficult than the task of fitting equation (8.1.1.1). The function of
is conceptually only slightly more difficult than the task of fitting equation (8.1.1.1). The function of  variables
variables
 equal to 0 , the set of normal equations is obtained for this least squares problem, generalizing the pair of equations from Part 7.1. There are
equal to 0 , the set of normal equations is obtained for this least squares problem, generalizing the pair of equations from Part 7.1. There are  . And typically, they can be solved simultaneously for a single set of values,
. And typically, they can be solved simultaneously for a single set of values,  , minimizing
, minimizing  version of equation (8.1.1.2)
version of equation (8.1.1.2)
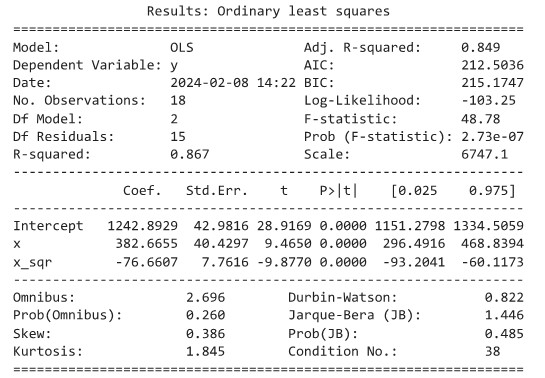





 produces
produces  . So
. So  of the raw variability in compressive strength is accounted for using the fitted quadratic. The sample correlation between the observed strengths
of the raw variability in compressive strength is accounted for using the fitted quadratic. The sample correlation between the observed strengths  and fitted strengths
and fitted strengths  is
is  .
. , and
, and  for each
for each 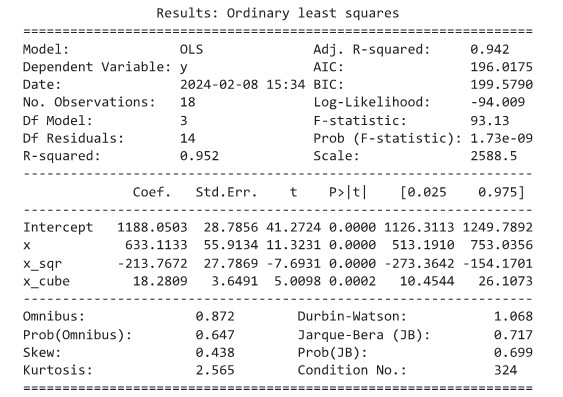

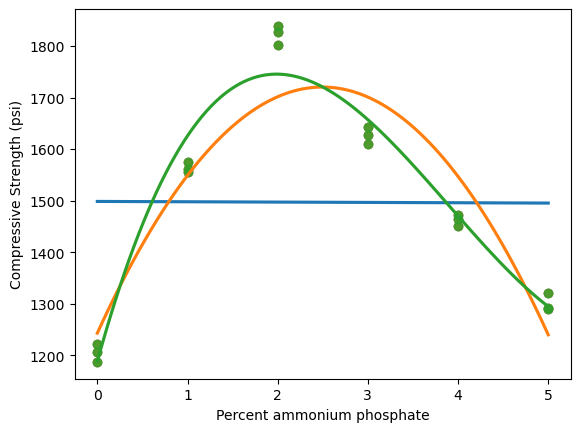
 . Unfortunately, this is where compressive strength is greatest—precisely the area of greatest practical interest.
. Unfortunately, this is where compressive strength is greatest—precisely the area of greatest practical interest. intervals beginning at some unknown time
intervals beginning at some unknown time  (less than
(less than 

 ) will be
) will be  . This is in fact how the value
. This is in fact how the value  , quoted in Section 1.4, was obtained.
, quoted in Section 1.4, was obtained.
 ) with
) with 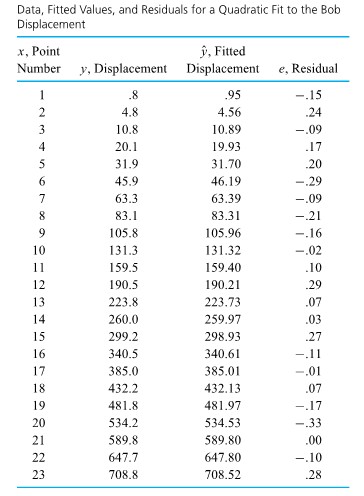

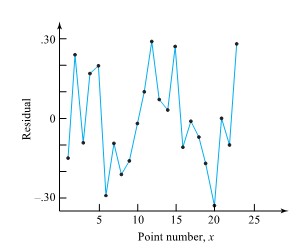
 current waveform is one matter to be addressed.
current waveform is one matter to be addressed. . But having identified the region around
. But having identified the region around  ammonium phosphate. It is quite possible that a quadratic fit only to data with
ammonium phosphate. It is quite possible that a quadratic fit only to data with  would be both adequate and helpful as a summarization of the follow-up data.
would be both adequate and helpful as a summarization of the follow-up data. in equation (8.1.1.2) can be replaced by any (known) functions of
in equation (8.1.1.2) can be replaced by any (known) functions of 

 that is linear in the parameters
that is linear in the parameters  and
and  . So, presented with a set of
. So, presented with a set of  (and thus
(and thus  and
and  .
. for some function
for some function  .
. . To illustrate its use in the present context, normal plots of both discovery times and log discovery times are given in Figure 8.1.2.2. These plots indicate that Elliot, Kibby, and Meyer could not have reasonably applied standard methods of inference to the discovery times, but they could have used the methods with log discovery times. The second normal plot is far more linear than the first.
. To illustrate its use in the present context, normal plots of both discovery times and log discovery times are given in Figure 8.1.2.2. These plots indicate that Elliot, Kibby, and Meyer could not have reasonably applied standard methods of inference to the discovery times, but they could have used the methods with log discovery times. The second normal plot is far more linear than the first.


 , transformation (8.1.2.1) tends to lengthen the right tail of a distribution for
, transformation (8.1.2.1) tends to lengthen the right tail of a distribution for  , the transformation tends to shorten the right tail of a distribution for
, the transformation tends to shorten the right tail of a distribution for 
 power of the response mean, try transformation (4.34) with
power of the response mean, try transformation (4.34) with  .
. versus
versus  and see if there is approximate linearity. If so, a slope of roughly 1 makes (1) appropriate, while a slope of
and see if there is approximate linearity. If so, a slope of roughly 1 makes (1) appropriate, while a slope of  signals what version of (2) might be helpful.
signals what version of (2) might be helpful.
 data points are pictured in three dimensions, along with a possible fitted surface of the form (8.1.3.1). To fit a surface defined by equation (8.1.3.1) to a set of
data points are pictured in three dimensions, along with a possible fitted surface of the form (8.1.3.1). To fit a surface defined by equation (8.1.3.1) to a set of  via least squares, the function of
via least squares, the function of 
 .
.
 , is the percent circulating minus 50 times 10 . The response variable,
, is the percent circulating minus 50 times 10 . The response variable,  , and
, and 
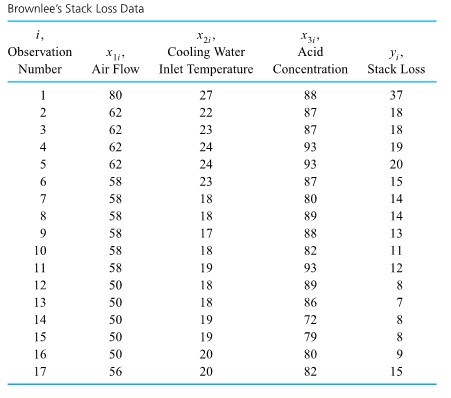

 . The coefficients in this equation can be thought of as rates of change of stack loss with respect to the individual variables
. The coefficients in this equation can be thought of as rates of change of stack loss with respect to the individual variables  can be interpreted as the increase in stack loss
can be interpreted as the increase in stack loss  is positive indicates that the higher the rate at which the plant is run, the larger
is positive indicates that the higher the rate at which the plant is run, the larger 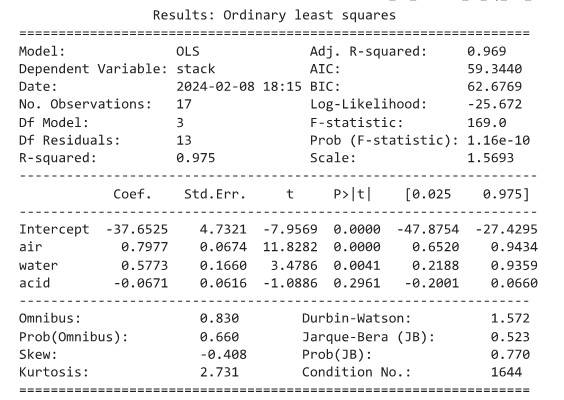

 data to “see” how an equation is fitting. About all that we can do at this point is to (1) offer the broad advice that what is wanted is the simplest equation that adequately fits the data and then (2) provide examples of how
data to “see” how an equation is fitting. About all that we can do at this point is to (1) offer the broad advice that what is wanted is the simplest equation that adequately fits the data and then (2) provide examples of how  of the raw variability in stack loss. Inclusion of
of the raw variability in stack loss. Inclusion of 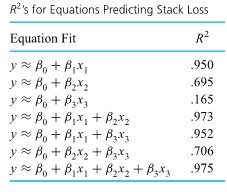

 the fitted rate of change in
the fitted rate of change in 
 , and
, and  in equation (8.1.3.3) differ somewhat from the corresponding values in equation (8.1.3.2). That is, equation (8.1.3.3) was not obtained from equation
in equation (8.1.3.3) differ somewhat from the corresponding values in equation (8.1.3.2). That is, equation (8.1.3.3) was not obtained from equation will change depending on which
will change depending on which  term to the fitted equation (8.1.3.3).
term to the fitted equation (8.1.3.3).

 and residuals that show even less of a pattern than those for the fitted equation (8.1.3.3). In particular, the hint of curvature on the plot of residuals versus
and residuals that show even less of a pattern than those for the fitted equation (8.1.3.3). In particular, the hint of curvature on the plot of residuals versus ![x_{3}[latex] and equation (8.1.3.4) does not.</div> </div> <div>.</div> <div> [caption id="attachment_450" align="aligncenter" width="546"]<img class="wp-image-450 size-full" src="https://ecampusontario.pressbooks.pub/app/uploads/sites/4023/2024/02/120_1.jpg" alt="" width="546" height="454" /> Figure 8.1.3.2 Plots of residuals from a two-variable equation fit to the stack loss data ( yˆ =−42.00 − .78x1 + .57x2 )[/caption] . Equation (8.1.3.4) is somewhat more complicated than equation (8.1.3.3). But because it still really only involves two different input [latex]x x_{3}[latex] and equation (8.1.3.4) does not.</div> </div> <div>.</div> <div> [caption id="attachment_450" align="aligncenter" width="546"]<img class="wp-image-450 size-full" src="https://ecampusontario.pressbooks.pub/app/uploads/sites/4023/2024/02/120_1.jpg" alt="" width="546" height="454" /> Figure 8.1.3.2 Plots of residuals from a two-variable equation fit to the stack loss data ( yˆ =−42.00 − .78x1 + .57x2 )[/caption] . Equation (8.1.3.4) is somewhat more complicated than equation (8.1.3.3). But because it still really only involves two different input [latex]x](https://atu0g9ctah.execute-api.ca-central-1.amazonaws.com/latest/latex?latex=x_%7B3%7D%5Blatex%5D%20and%20equation%20%288.1.3.4%29%20does%20not.%3C%2Fdiv%3E%20%20%3C%2Fdiv%3E%20%20%3Cdiv%3E.%3C%2Fdiv%3E%20%20%3Cdiv%3E%20%20%20%20%5Bcaption%20id%3D%22attachment_450%22%20align%3D%22aligncenter%22%20width%3D%22546%22%5D%3Cimg%20class%3D%22wp-image-450%20size-full%22%20src%3D%22https%3A%2F%2Fecampusontario.pressbooks.pub%2Fapp%2Fuploads%2Fsites%2F4023%2F2024%2F02%2F120_1.jpg%22%20alt%3D%22%22%20width%3D%22546%22%20height%3D%22454%22%20%2F%3E%20Figure%208.1.3.2%20Plots%20of%20residuals%20from%20a%20two-variable%20equation%20%EF%AC%81t%20to%20the%20stack%20loss%20data%20%28%20y%CB%86%20%3D%E2%88%9242.00%20%E2%88%92%20.78x1%20%2B%20.57x2%20%29%5B%2Fcaption%5D%20%20%20%20.%20%20%20%20Equation%20%288.1.3.4%29%20is%20somewhat%20more%20complicated%20than%20equation%20%288.1.3.3%29.%20But%20because%20it%20still%20really%20only%20involves%20two%20different%20input%20%5Blatex%5Dx&fg=000000&font=TeX&svg=1) 's and also eliminates the slight pattern seen on the plot of residuals for equation (8.1.3.3) versus
's and also eliminates the slight pattern seen on the plot of residuals for equation (8.1.3.3) versus 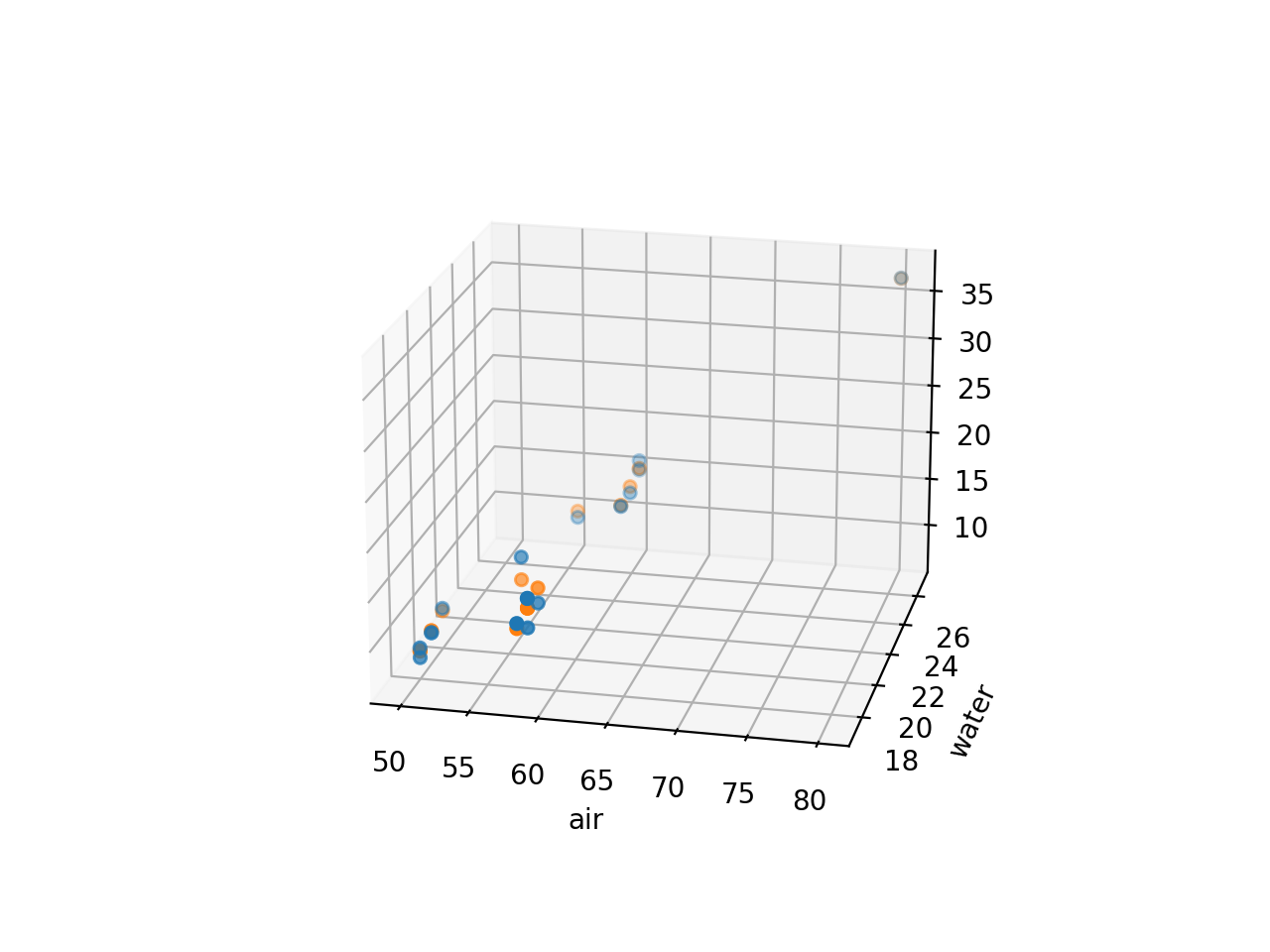
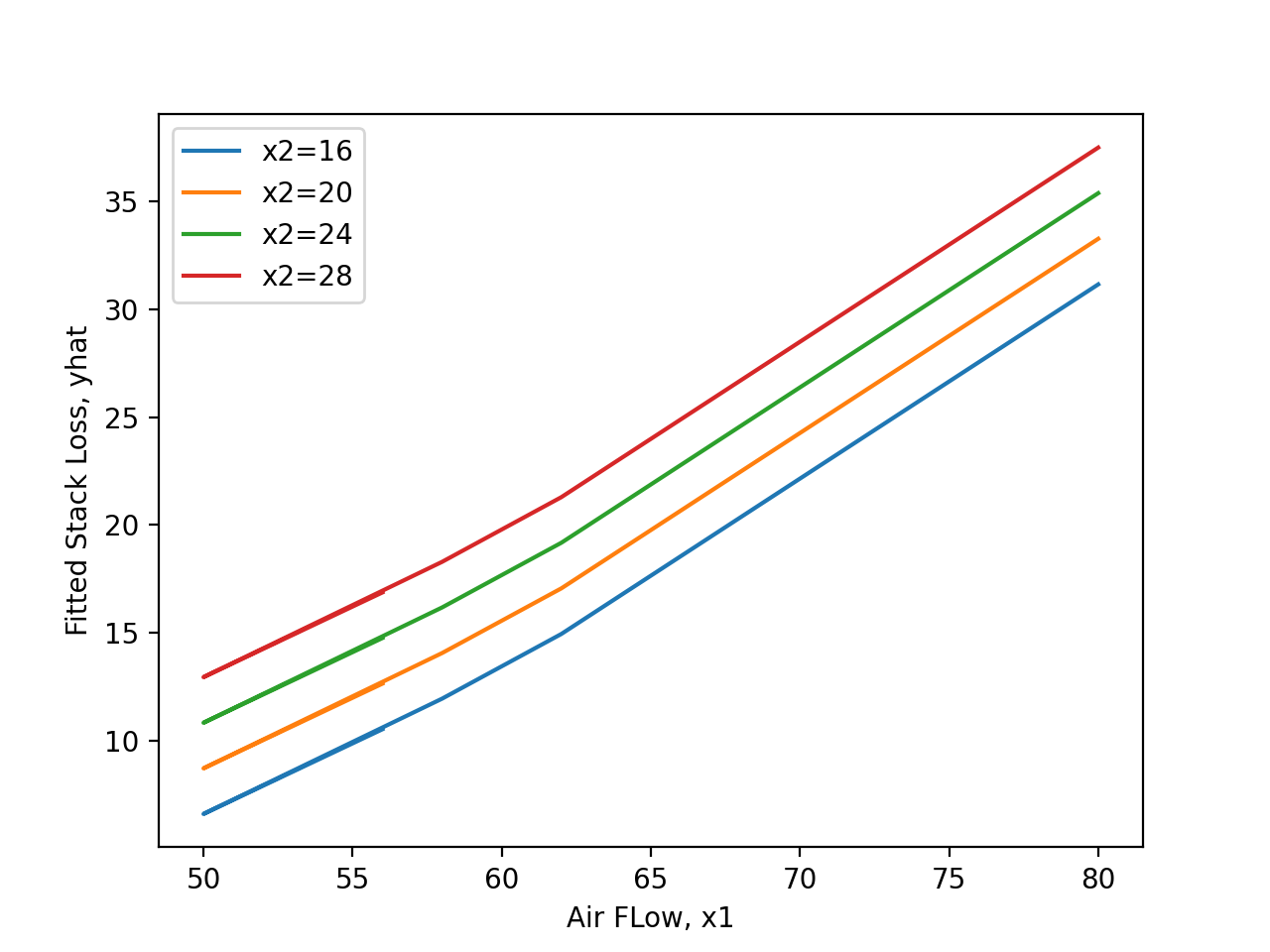
 canard placement in inches above the plane defined by the main wing
canard placement in inches above the plane defined by the main wing tail placement in inches above the plane defined by the main wing
tail placement in inches above the plane defined by the main wing


 and the fitted relationship
and the fitted relationship
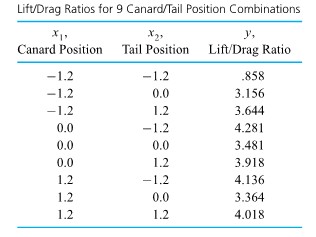
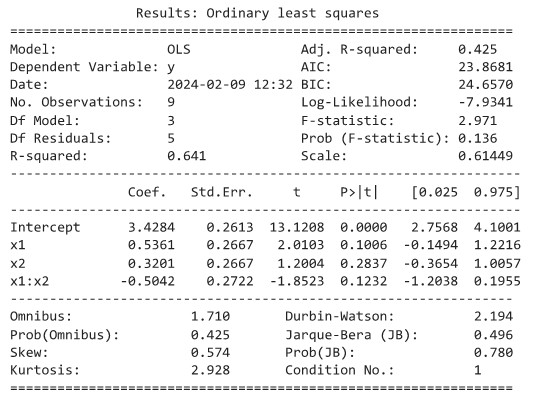
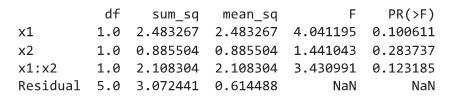

 products were created and
products were created and  surface would be parallel for various
surface would be parallel for various 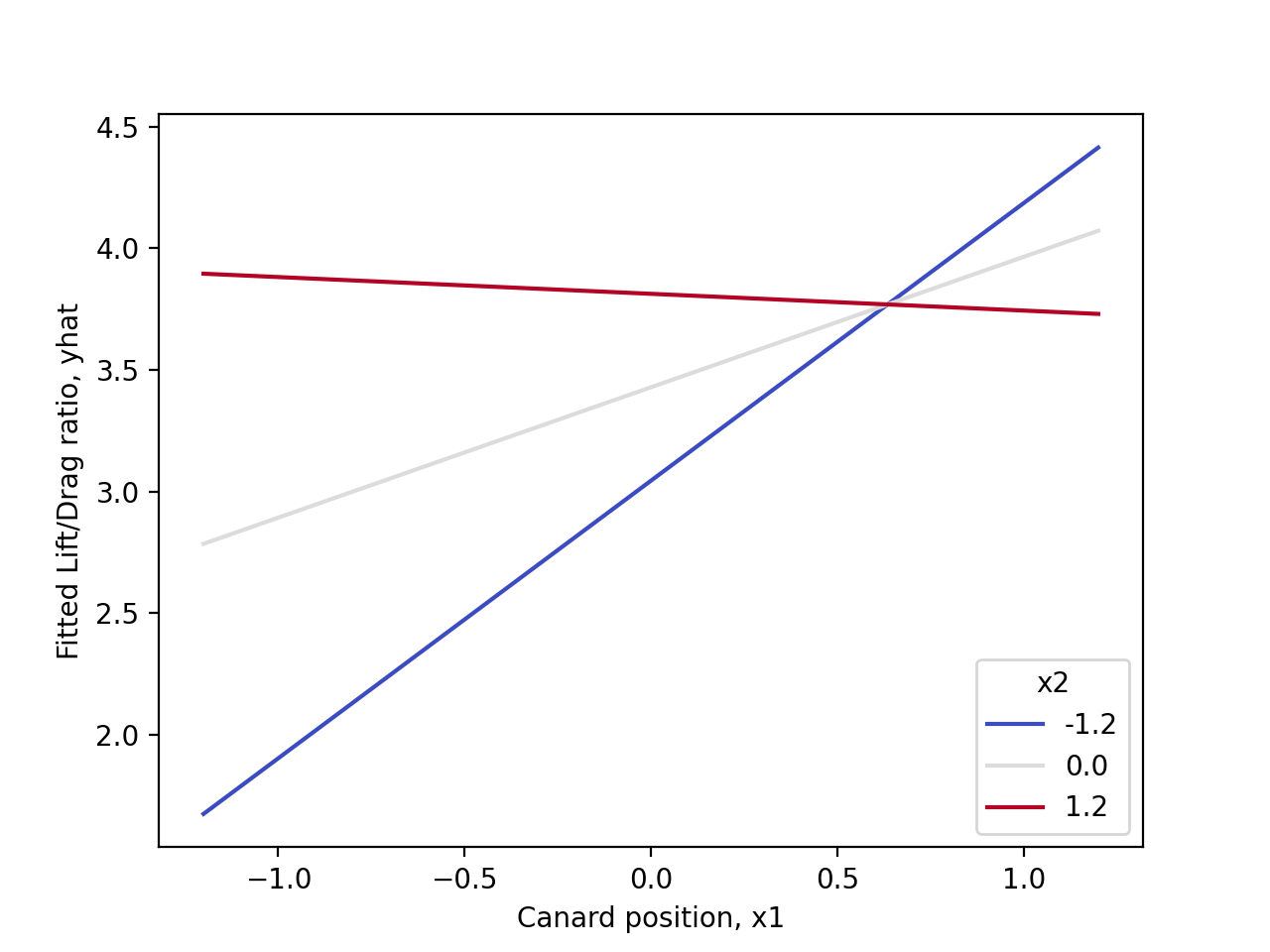

 and generally random-looking residuals. It can be verified by plotting
and generally random-looking residuals. It can be verified by plotting 
 pairs for the data in Table 8.1.3. It shows that by most qualitative standards, observation 1 in Table 8.1.3. is unusual or outlying.
pairs for the data in Table 8.1.3. It shows that by most qualitative standards, observation 1 in Table 8.1.3. is unusual or outlying.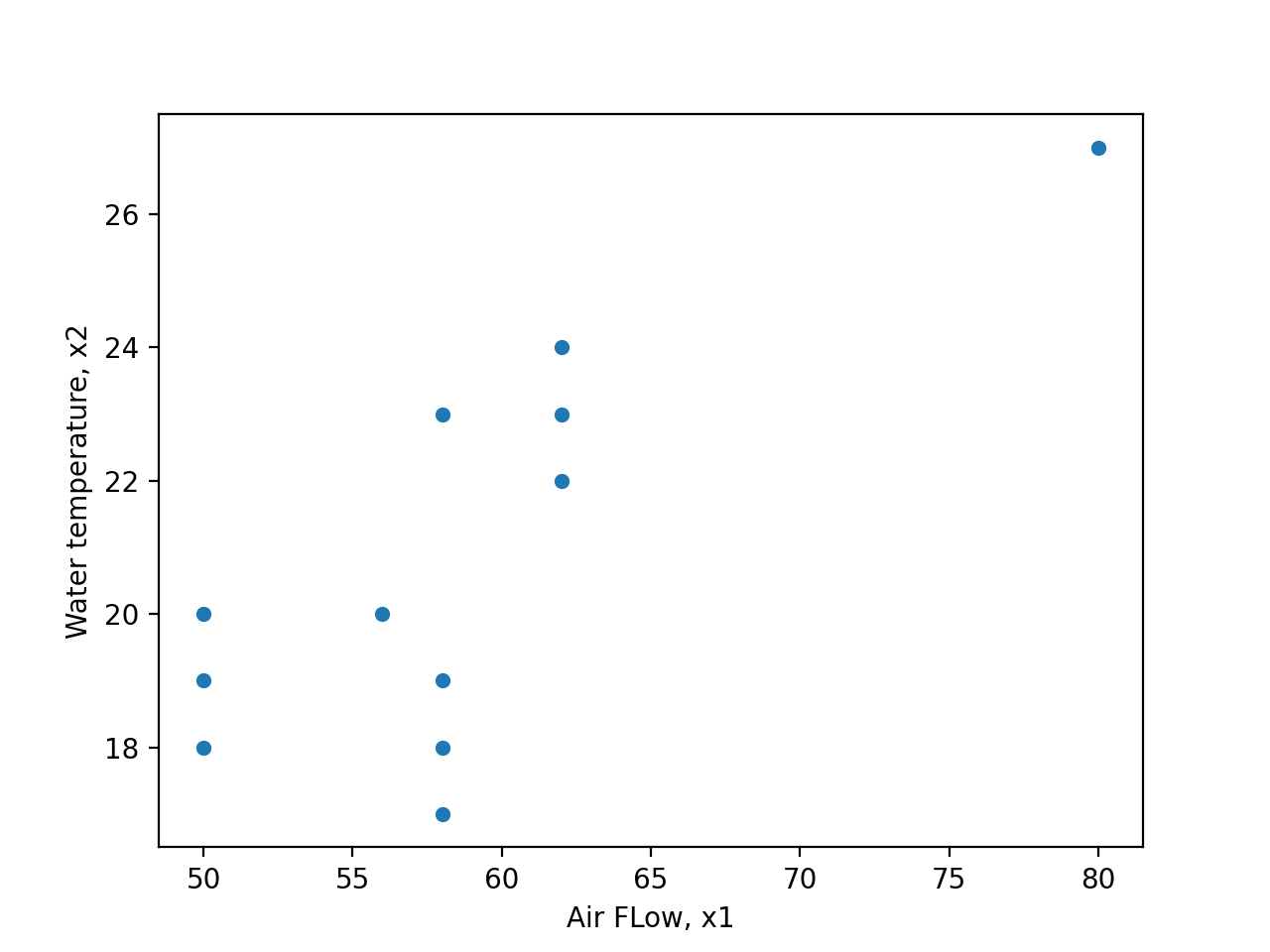

 are obtained. Using equation (8.1.61) as a description of stack loss and limiting attention to
are obtained. Using equation (8.1.61) as a description of stack loss and limiting attention to  version of a polynomial through each of these points. But in most physical problems, such a curve would do a much worse job of predicting
version of a polynomial through each of these points. But in most physical problems, such a curve would do a much worse job of predicting  codes for each category except the referent group (which is omitted). Several examples of categorical variables that can be represented in multiple regression with dummy variables include:
codes for each category except the referent group (which is omitted). Several examples of categorical variables that can be represented in multiple regression with dummy variables include: , control
, control  for the “dummied” group. This is illustrated in Figure 8.2.1.1. In this illustration, the value of
for the “dummied” group. This is illustrated in Figure 8.2.1.1. In this illustration, the value of  (a continuous variable) and
(a continuous variable) and  (a dummy variable). When
(a dummy variable). When  , the value of
, the value of 
 .
. .
. women,
women,  men
men  could be interacted with ideology
could be interacted with ideology  strong liberal,
strong liberal,  strong conservative) to predict levels of perceived risk of climate change (
strong conservative) to predict levels of perceived risk of climate change (  no risk,
no risk,  extreme risk). If your hypothesized interaction was correct, you would observe the kind of pattern as shown in Figure 8.2.1.2.
extreme risk). If your hypothesized interaction was correct, you would observe the kind of pattern as shown in Figure 8.2.1.2.
 . Using matrix notation, the same equation can be expressed in a more compact and (believe it or not!) intuitive form:
. Using matrix notation, the same equation can be expressed in a more compact and (believe it or not!) intuitive form:  .
. . In the following example,
. In the following example, ![A_{m, n}=\left[\begin{array}{cccc}a_{1,1} & a_{1,2} & \cdots & a_{1, n} \\ a_{2,1} & a_{2,2} & \cdots & a_{2, n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m, 1} & a_{m, 2} & \cdots & a_{m, n}\end{array}\right] A_{m, n}=\left[\begin{array}{cccc}a_{1,1} & a_{1,2} & \cdots & a_{1, n} \\ a_{2,1} & a_{2,2} & \cdots & a_{2, n} \\ \vdots & \vdots & \ddots & \vdots \\ a_{m, 1} & a_{m, 2} & \cdots & a_{m, n}\end{array}\right]](https://atu0g9ctah.execute-api.ca-central-1.amazonaws.com/latest/latex?latex=A_%7Bm%2C%20n%7D%3D%5Cleft%5B%5Cbegin%7Barray%7D%7Bcccc%7Da_%7B1%2C1%7D%20%26%20a_%7B1%2C2%7D%20%26%20%5Ccdots%20%26%20a_%7B1%2C%20n%7D%20%5C%5C%20a_%7B2%2C1%7D%20%26%20a_%7B2%2C2%7D%20%26%20%5Ccdots%20%26%20a_%7B2%2C%20n%7D%20%5C%5C%20%5Cvdots%20%26%20%5Cvdots%20%26%20%5Cddots%20%26%20%5Cvdots%20%5C%5C%20a_%7Bm%2C%201%7D%20%26%20a_%7Bm%2C%202%7D%20%26%20%5Ccdots%20%26%20a_%7Bm%2C%20n%7D%5Cend%7Barray%7D%5Cright%5D&fg=000000&font=TeX&svg=1)
![A=\left[\begin{array}{ccc}10 & 5 & 8 \\ -12 & 1 & 0\end{array}\right] A=\left[\begin{array}{ccc}10 & 5 & 8 \\ -12 & 1 & 0\end{array}\right]](https://atu0g9ctah.execute-api.ca-central-1.amazonaws.com/latest/latex?latex=A%3D%5Cleft%5B%5Cbegin%7Barray%7D%7Bccc%7D10%20%26%205%20%26%208%20%5C%5C%20-12%20%26%201%20%26%200%5Cend%7Barray%7D%5Cright%5D&fg=000000&font=TeX&svg=1)
 and
and  .
.![A=\left[\begin{array}{c}6 \\ -1 \\ 8 \\ 11\end{array}\right] A=\left[\begin{array}{c}6 \\ -1 \\ 8 \\ 11\end{array}\right]](https://atu0g9ctah.execute-api.ca-central-1.amazonaws.com/latest/latex?latex=A%3D%5Cleft%5B%5Cbegin%7Barray%7D%7Bc%7D6%20%5C%5C%20-1%20%5C%5C%208%20%5C%5C%2011%5Cend%7Barray%7D%5Cright%5D&fg=000000&font=TeX&svg=1)
![A=\left[\begin{array}{llll}1 & 2 & 8 & 7\end{array}\right] A=\left[\begin{array}{llll}1 & 2 & 8 & 7\end{array}\right]](https://atu0g9ctah.execute-api.ca-central-1.amazonaws.com/latest/latex?latex=A%3D%5Cleft%5B%5Cbegin%7Barray%7D%7Bllll%7D1%20%26%202%20%26%208%20%26%207%5Cend%7Barray%7D%5Cright%5D&fg=000000&font=TeX&svg=1)

 Surface Roughness and
Surface Roughness and  Water Contact Angle):
Water Contact Angle):


 has only non-zero values on the diagonal. Therefore:
has only non-zero values on the diagonal. Therefore:



 , can be interpreted the same manner as before. For example, a 1 unit increase in roughness corresponds to a 16.25 a.u. increase in cell viability. This method also explains why we had to divide by 2 a second time earlier since this coefficient represents the effect of changing surface roughness from 0 to 1 or from 325 to 350 µm. The same is true for water contact angle as well. Finally, the interaction term decreases cell viability by 3.25 units if both surface roughness and water contact angle are at the same level (both high or both low).
, can be interpreted the same manner as before. For example, a 1 unit increase in roughness corresponds to a 16.25 a.u. increase in cell viability. This method also explains why we had to divide by 2 a second time earlier since this coefficient represents the effect of changing surface roughness from 0 to 1 or from 325 to 350 µm. The same is true for water contact angle as well. Finally, the interaction term decreases cell viability by 3.25 units if both surface roughness and water contact angle are at the same level (both high or both low).
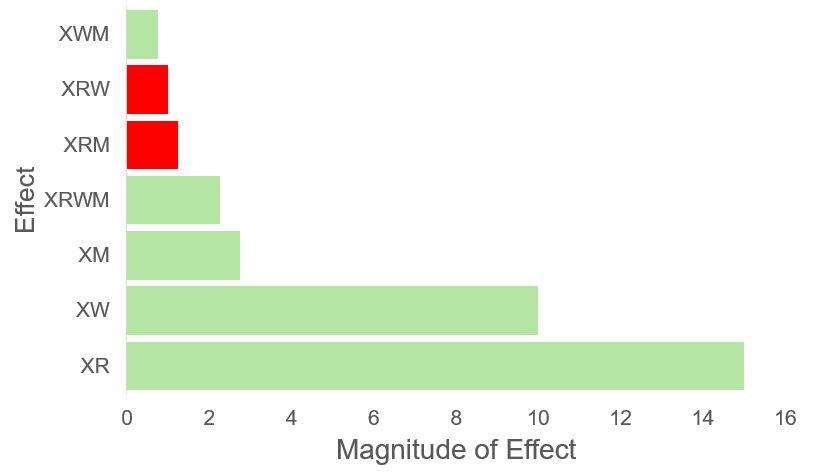
 Material Coefficient):
Material Coefficient):

 ABC interaction effect + disturbance.
ABC interaction effect + disturbance. ) will now be confounded with an interaction term.
) will now be confounded with an interaction term.


 is confounded with the interaction of
is confounded with the interaction of  , since the model coefficient is the sum of these two effects. From this we can state that
, since the model coefficient is the sum of these two effects. From this we can state that  is an alias for
is an alias for  , that
, that  is an alias for
is an alias for  and that the intercept is aliased with the 3-factor interaction
and that the intercept is aliased with the 3-factor interaction 



 . Factors
. Factors  . This is called the generating relation.
. This is called the generating relation. is a column of ones.
is a column of ones.

 . Take the generating relation and multiply both sides by Through some algebra we can also establish the defining relation of
. Take the generating relation and multiply both sides by Through some algebra we can also establish the defining relation of  by the following equation:
by the following equation:
 which tells us that
which tells us that 
 . Here the roman numerals
. Here the roman numerals  indicate the level of resolution for the design. This number is equivalent to the number of factors present in the defining relation. Since
indicate the level of resolution for the design. This number is equivalent to the number of factors present in the defining relation. Since 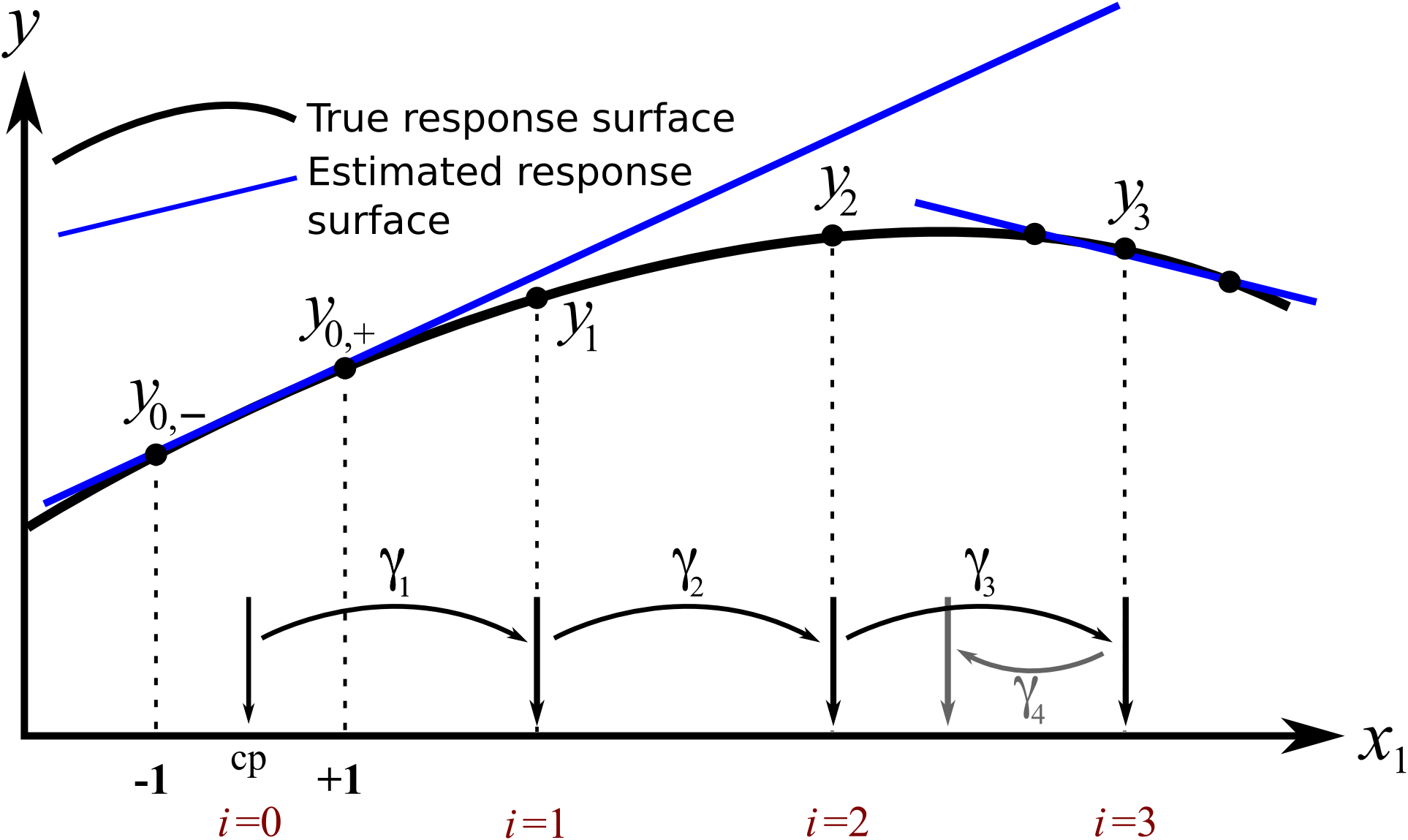












 .
.