Mathématiques pour les gens de métier Volume 1 Copyright © 2023 by eCampusOntario is licensed under a Licence Creative Commons Attribution 4.0 International, except where otherwise noted.
Mathématiques pour les gens de métier Volume 1 Copyright © 2023 by eCampusOntario is licensed under a Licence Creative Commons Attribution 4.0 International, except where otherwise noted.
1
Mathématiques pour les gens de métier: Le volume 1 de Chad Flinn et Mark Overgaard, est protégé par une licence internationale Creative Commons Attribution 4.0, sauf indication contraire.
© 2020 Chad Flinn et Mark Overgaard
La licence CC vous permet de conserver, réutiliser, copier, redistribuer et réviser ce livre — en tout ou en partie — gratuitement, à condition que les auteurs soient cités comme suit :
Si vous redistribuez la totalité ou une partie de ce livre, il est recommandé d’ajouter l’énoncé suivant à la page du droit d’auteur afin que les lecteurs puissent accéder gratuitement au livre original :
Télécharger gratuitement à partir de B.C. Open Textbook Collection.
Note sur les images utilisées dans ce texte
Sauf indication contraire, toutes les images incluses dans le présent texte proviennent de Pixabay (à l’exception des images d’équations). Pixabay propose une vaste collection d’images gratuites disponibles sous la licence Pixabay. La licence Pixabay autorise l’utilisation et la modification des images à des fins commerciales et non commerciales sans qu’il soit nécessaire de les attribuer.
Exemple de citation de style APA :
Ce manuel peut être référencé. Selon les normes de citation APA, il se présenterait comme suit :
Attribution de l’image de couverture :
Fractals by insspirito on Pixabay.
ISBN version électronique : 978-1-77420-061-2
ISBN version imprimé : 978-1-77420-060-5
Visitez BCcampus Open Education pour en savoir plus sur l’éducation ouverte en Colombie-Britannique.
Ce livre a été produit en collaboration avec Pressbooks.
2
3
La version Web de la présente ressource a été conçue pour répondre aux Directives pour l’accessibilité aux contenus Web 2.0,, niveau AA. En outre, elle respecte toutes les lignes directrices de l’Annexe A : Liste de contrôle pour l’accessibilité de la Boîte à outils d’accessibilité – 2e édition. Cette liste comprend les éléments suivants :
Le son des vidéos ne fournit pas toujours une description de ce qui se passe visuellement dans les vidéos.
Nous nous efforçons en permanence de rendre nos manuels plus accessibles. Si vous avez des difficultés à accéder à ce manuel, veuillez nous contacter pour nous en informer afin que nous puissions résoudre le problème.
Veuillez fournir les renseignements suivants :
Vous pouvez nous contacter de l’une des manières suivantes :
La dernière mise à jour de la présente déclaration remonte au 8 avril 2020.
4
Vous pouvez accéder au manuel en ligne et télécharger gratuitement tous les formats ici : Mathématiques pour les gens de métier : Volume 1. Pour télécharger le livre dans un format différent, recherchez le menu déroulant « Télécharger ce livre » et sélectionnez le type de fichier souhaité.
| Format | Internet requis? | Appareil | Applications requises | Caractéristiques d’accessibilité | Compatible avec les lecteurs d’écran |
|---|---|---|---|---|---|
| Livre Web en ligne | Oui | Ordinateur, tablette, téléphone | Un navigateur Internet (Chrome, Firefox, Edge ou Safari) | Conformité WCAG 2.0 AA, possibilité d’agrandir le texte et compatibilité avec les outils de synthèse vocale du navigateur, vidéos sous-titrées | Oui |
| Non | Ordinateur, copie imprimée | Adobe Reader (pour lecture sur ordinateur) ou une imprimante | Possibilité de mettre en surbrillance et d’annoter le texte. Si vous lisez sur l’ordinateur, vous pouvez faire un zoom avant. | Incertain | |
| EPUB et MOBI | Non | Ordinateur, tablette, téléphone | Application Kindle (MOBI) ou application eReader (EPUB) | Possibilité d’agrandir le texte, de modifier le style, la taille et la couleur de la police. | Incertain |
| HTML | Non | Ordinateur, tablette, téléphone | Un navigateur Internet (Chrome, Firefox, Edge ou Safari) | Conformité WCAG 2.0 AA et compatible avec les outils de synthèse vocale des navigateurs. | Oui |
Le livre Web comprend un certain nombre d’éléments interactifs et multimédias. Il s’agit notamment de vidéos de démonstration des questions pratiques et de jeux-questionnaires interactifs proposés à la fin de chaque chapitre. Les vidéos et les questionnaires interactifs ne seront pas inclus si vous n’utilisez pas le livre Web. Votre copie du texte fournira plutôt un lien vous permettant d’accéder à ces éléments interactifs.
Cependant, les activités interactives et les réponses aux vidéos sont également fournies dans des formats alternatifs pour les personnes qui n’utilisent pas le livre Web. En ce qui concerne les réponses aux vidéos, elles se trouvent également dans l’Annexe B : Réponses aux questions pratiques. Quant aux questionnaires des chapitres, ils sont disponibles dans un format statique dans l’Annexe C : Copies hors ligne des questionnaires des chapitres.
Même si vous décidez d’utiliser une version PDF ou imprimée du manuel, vous pouvez accéder au livre Web et télécharger d’autres formats à tout moment.
5
Les ressources éducatives libres (RÉL) sont des ressources d’enseignement, d’apprentissage et de recherche qui, grâce aux autorisations accordées par le détenteur des droits d’auteur, permettent à d’autres personnes de les utiliser, de les distribuer, de les conserver ou d’y apporter des modifications. Nos manuels scolaires à accès libre sont sous licence Creative Commons et sont proposés gratuitement dans différents formats de livres électroniques ou sous forme de livres imprimés disponibles à prix coûtant.
Pour plus d’informations sur l’éducation ouverte en Colombie-Britannique, veuillez consulter le site Web BCampus Open Education. Si vous êtes un enseignant qui utilise ce livre dans le cadre d’un cours, veuillez remplir notre formulaire Adoption d’un manuel libre.
Le guide de style ci-joint a été utilisé pour l’édition du présent livre : Feuille de style pour Mathématiques pour les gens de métier [fichier Word]
6
Un élément BCcampus a été exclu de cette version du texte. Vous pouvez le consulter en ligne ici : https://opentextbc.ca/mathfortrades1/?p=26
Bienvenue à tous dans cette vidéo d’introduction aux mathématiques pour les métiers!
Apprendre les mathématiques, n’est-ce pas comparable au fait d’apprendre une nouvelle langue? Elles ont leur propre vocabulaire, leurs propres phrases, leur propre structure et leurs propres règles.
Eh bien, dans ce manuel Mathématiques pour les gens de métier : Volume 1, nous allons commencer à construire tout cela. Nous allons construire les mots. Nous allons nous servir des mots pour construire des phrases. Nous allons trouver les règles, nous allons créer une structure, et nous allons le faire par étapes.
Vous pouvez considérer le Chapitre 1 comme première étape. Il porte sur les « Nombres entiers ». Une fois que nous l’avons parcouru, nous passons au Chapitre 2, « Fractions ». Chapitre 3, une autre étape, « Nombres décimaux ». Et enfin, le Chapitre 4, « Les pourcentages ».
Alors, quand vous parcourez ce livre, il y a plusieurs choses auxquelles vous devez penser. Tout d’abord, prenez votre temps, mais soyez efficace. N’oubliez pas qu’il s’agit de vous. Que voulez-vous en retirer? Par exemple, si vous constatez que vous connaissez les nombres entiers et que vous n’avez pas besoin de parcourir ce livre, c’est parfait. Parfaite. Ne le faites pas. Par contre, vous pourriez avoir besoin d’un peu plus d’aide pour les fractions. Dans ce cas, consultez la partie consacrée aux fractions. Il s’agit de vous, et c’est pour vous, alors faites ce qui vous convient.
Suivez les étapes. Les exemples sont présentés par étapes. Suivez ces étapes, elles constituent la clé. Cela vous aidera à passer de l’étape 1 à l’étape 4 ou 5 et à comprendre le processus entre les deux.
Pensez aux concepts et aux corrélations. En mathématiques, tout est lié, donc plus vous comprenez les concepts et les corrélations, plus vous vous facilitez la tâche.
Regardez les vidéos après avoir répondu aux questions. Il s’agit de la partie la plus intéressante du présent livre. Vous trouverez des vidéos partout dans le livre [indique une icône vidéo de Mathématiques pour les gens de métier] et il s’agit de réponses vidéo. Donc, lorsque nous vous proposons des questions pratiques, sortez votre stylo ou votre crayon, sortez votre papier et exercez-vous. Pensez à ce que vous êtes en train de faire ou au processus que vous êtes en train de suivre pendant que vous vous exercez. Puis vérifiez les réponses. Comparez avec ce que vous avez fait.
Étudiez également dans un environnement sans distraction. Pas de téléphone, pas de télévision, rien de tout cela. Cela vous aidera vraiment parce que vous serez à fond dans votre travail, ce qui vous permettra de passer à l’étape suivante.
Concentrez-vous pendant 20 à 30 minutes, à 110 %, puis faites une pause. Cela vous aidera probablement à retenir plus d’informations et à être plus efficace dans votre temps d’étude. Sommes-nous d’accord? 20 à 30 minutes.
Autre chose, et c’est la plus importante, car si vous ne le faites pas, les choses deviendront de plus en plus difficiles. Amusez-vous. Appréciez le processus.
I
II
Nombres entiers
Objectifs
· Distinguer les chiffres des nombres entiers.
· Localiser les chiffres dans le système de valeurs de position
· Additionner des nombres entiers.
· Soustraire des nombres entiers
· Multiplier des nombres entiers.
· Diviser des nombres entiers.
1
1.
Le système de valeur de position
Avez-vous déjà entendu l’expression « nombre entier »? Cela peut sembler un concept étrange : les chiffres ne sont-ils pas tous entiers? J’ai mangé six pommes cette semaine, ou j’ai chargé mon véhicule électrique pendant trois heures hier. Ce sont des chiffres entiers, n’est-ce pas?
Eh bien, les chiffres ne sont pas tous entiers. Vous auriez pu manger 3½ pommes pendant une semaine où vous mangiez très peu de pommes, et vous n’avez peut-être pas conduit votre véhicule électrique aussi longtemps hier, alors vous n’avez eu à le recharger que pendant 2,3 heures. Ce ne sont pas des chiffres entiers.
Le but de ce chapitre est de définir ce qu’est un nombre entier et d’apprendre ensuite à travailler avec ces nombres entiers, que ce soit en les additionnant, en les soustrayant, en les multipliant ou en les divisant.
Tous les chapitres de ce manuel, notamment celui-ci, contiendront des exemples et des exercices axés sur les métiers. Ils contiennent des renseignements pertinents pour tous les métiers, peu importe le métier.
Il y a quelques années, un étudiant du nom de Harpreet a suivi un programme d’apprentissage en plomberie. Après avoir terminé ses études et reçu sa désignation Sceau rouge comme plombier, il a décidé d’ouvrir sa propre entreprise de plomberie.
Comme la plupart des nouveaux entrepreneurs, il a connu une forte courbe d’apprentissage, surtout lorsqu’il s’agissait de commander du matériel pour des travaux et d’organiser et de planifier des horaires lorsqu’il avait plusieurs travaux en même temps.
Même s’il ne pensait peut-être pas compter des chiffres ou des nombres entiers, il a fini par travailler avec ces derniers lorsqu’il a commandé des matériaux et pendant les activités quotidiennes de l’entreprise.
Si nous voulons commencer par les éléments de base, nous devons commencer par les chiffres, que l’on appelle parfois nombres naturels. Ce sont les unités les plus élémentaires en algèbre et celles que nous utilisons pour compter les objets. Par exemple, Harpreet a dû commander une toilette, deux ensembles de robinets, trois raccords, quatre tuyaux tressés et cinq tablettes de chocolat (il semble que Harpreet ait un bec sucré).
Autre chose : dans les chiffres, il n’y a pas de parties décimales ou de fractions. De plus, il n’y a pas de négatif ni de zéro.
D’accord. Il n’y a donc pas de zéro. Mais que se passerait-il si nous décidions d’ajouter un zéro à l’ensemble des chiffres? Est-ce que ce serait si mauvais? Non, cela ne serait pas si terrible, mais nous ne pourrions plus dire que nous comptons des chiffres. L’ensemble des chiffres en ajoutant zéro devient ce qu’on appelle l’ensemble de nombres entiers.
Chiffres : 1, 2, 3, 4, 5,…
Nombres entiers : 0, 1, 2, 3, 4, 5,…
La découverte du zéro a été un grand pas dans l’histoire des mathématiques. Ne me demandez pas pourquoi, mais il semble que ce soit le cas. Quant à Harpreet, espérons qu’il soumissionne correctement et que son profit ne sera pas nul.
Craignant de mal estimer la valeur des travaux, Harpreet décide qu’il a besoin d’aide pour estimer et soumissionner, ainsi que pour tenir les livres. Il appelle son ami Jamieson et lui demande s’il veut l’aider. Jamieson, qui travaille dans l’industrie de la plomberie depuis plusieurs années, a eu une blessure persistante au dos et il estime que ce pourrait être une bonne occasion de se reposer un peu et d’aider son ami en même temps.
Le premier travail pour lequel Jamieson soumissionne est de 931 $. Jetez un coup d’œil aux trois chiffres de 931 et remarquez où ils se trouvent. C’est très important, parce que si Jamieson avait inversé les chiffres, il aurait soumissionné pour 139 $ et aurait probablement perdu de l’argent.
L’écriture du bon nombre repose sur ce que notre système de nombres appelle le système de valeur de position. Le 9, le 3 et le 1 sont tous situés à différents endroits dans le grand nombre, et chacun d’eux est appelé un chiffre. Le fait de placer les chiffres au mauvais endroit pourrait entraîner un désastre lorsqu’il s’agit d’argent et dans de nombreuses autres situations.
Voici un exemple visuel : disons que je prends un portefeuille, que je l’ouvre et que je retire l’argent. Supposons que ce portefeuille ait deux billets de 100 $, trois billets de 20 $ et un billet de 5 $. Quel serait le montant total du portefeuille?
J’aurais :
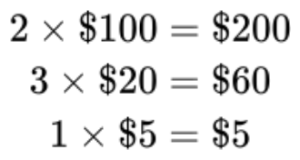
En faisant le total, j’aurais :
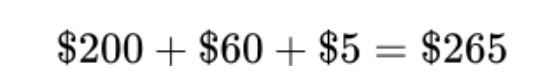
Remarquez que chacune des valeurs originales a une place précise dans le total. Le fait de placer les chiffres dans l’ordre inverse donnerait l’impression que nous avons beaucoup plus d’argent que nous en avons en réalité :
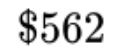
C’est l’importance du système de valeur des positions.
Un autre aspect de ce système est connu sous le concept de base 10. Chaque position dans un nombre est un endroit précis. Si on prend le nombre 265 comme exemple, on voit que :
5 = unités
6 = dizaines
2 = centaines
Chaque chiffre du système de valeurs de position peut avoir une valeur comprise entre zéro et neuf. Lorsque la valeur d’un chiffre dépasse 9, nous recommençons à zéro, mais nous ajoutons une valeur à la valeur du chiffre dans la deuxième valeur la plus élevée.
La façon la plus simple de voir les choses est de passer de 9 à 10 :
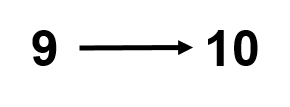
Dans ce cas-ci, les unités redeviennent zéro et les dizaines augmentent de 1.
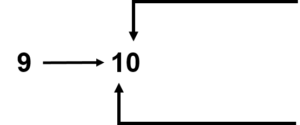
La valeur de l’unité est passée de neuf à zéro.
Il n’y avait pas de valeur dans les dizaines lorsque nous avons commencé, mais maintenant, les dizaines ont augmenté de 1.
Vous pensez peut-être que c’est vraiment trop simple à lire, mais ce sont les fondements du langage de l’algèbre. Bien que l’exemple utilisé ici soit assez simple, lorsque vous arrivez à des nombres plus grands et plus complexes, la grammaire mathématique que vous apprenez ici est la base pour comprendre une grammaire mathématique plus compliquée dans les chapitres à suivre.
Examinons maintenant un nombre plus élevé. Une façon de comprendre le système de valeur de la position est de prendre un nombre comme :
Si nous devions lire ce nombre, nous dirions :
Cinq milliards, deux cent dix-sept millions, trois cent soixante-quatre mille, neuf cent cinquante-huit.
On le lit ainsi parce que chaque chiffre correspond à une certaine valeur dans le système de valeur de la position. Jetez un coup d’œil au tableau de la valeur de la position suivant, dans lequel nous commençons par les unités et progressons vers le haut :
| Unités | 8 |
| Dizaines | 5 |
| Centaines | 9 |
| Milliers | 4 |
| Dix milliers | 6 |
| Centaines de milliers | 3 |
| Millions | 7 |
| Dix millions | 1 |
| Centaines de millions | 2 |
| Milliards | 5 |
| Dix milliards | – |
| Centaines de milliards | – |
Cette tendance se poursuivrait dans les billions, les billiards, les trillions, et ainsi de suite.
Le tableau ci-dessous illustre une autre façon courante d’exprimer les nombres dans le système de valeurs de la position.
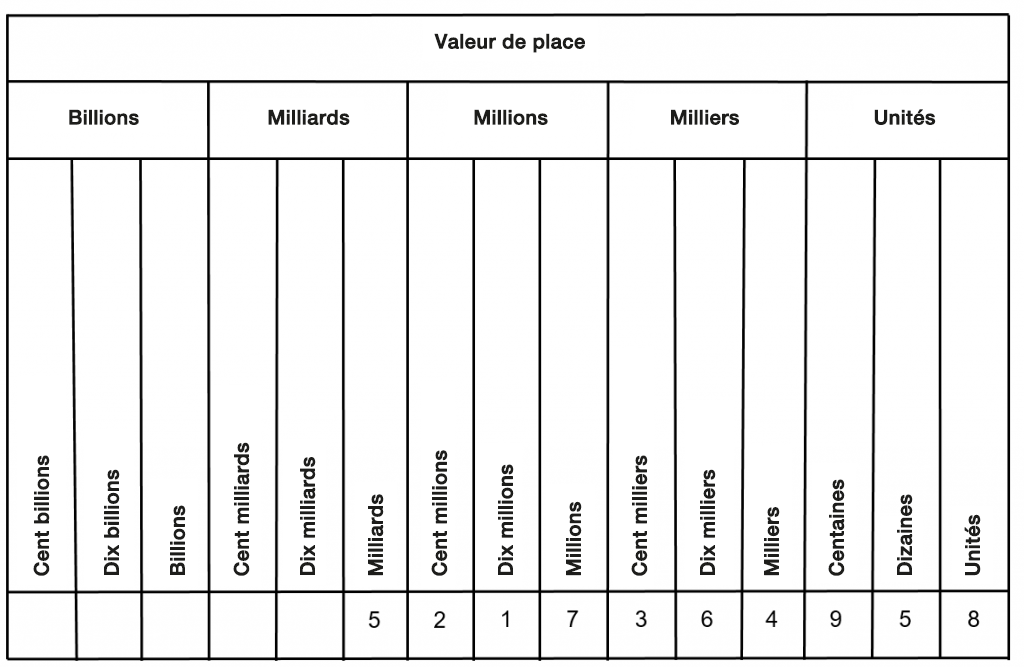
De gauche à droite, on obtient :
Essayez un exemple.
En répondant à cette question, pensez à la valeur réelle de chacun des chiffres. Par exemple, les 4 à la gauche du nombre ci-dessous représentent 40 000 000. Cela vous aidera à visualiser la valeur que chaque nombre représente réellement.
Trouvez la valeur de position de chacun des chiffres suivants :
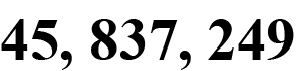
Utilisez la mise en page suivante comme guide pour vous aider à répondre à la question.
4 = ___________________
5 = ____________________
8 =____________________
3 =____________________
7 =____________________
2 = ____________________
4 = ____________________
9 = ____________________
Insérer les chiffres dans le tableau ci-dessous est également un bon point de départ :
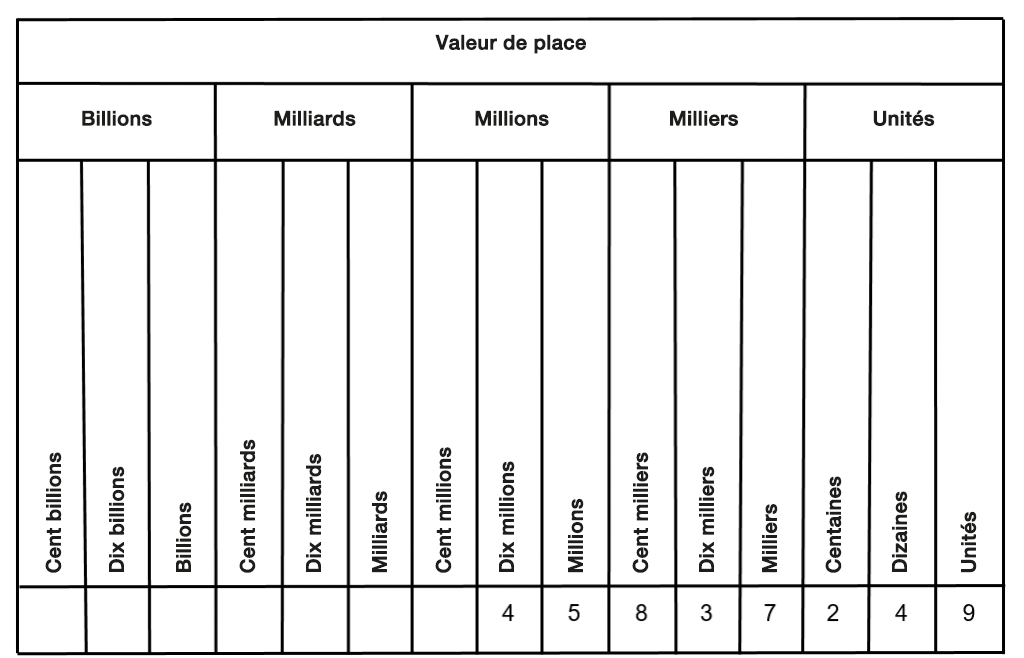
Solution :
En utilisant le tableau ci-dessus, vous obtenez :
4 = dix millions
5 = millions
8 = centaines de milliers
3 = dizaines de milliers
7 = milliers
2 = centaines
4 = dizaines
9 = unités
Essayez quelques autres exemples et jetez un coup d’œil aux réponses de la vidéo.
Trouvez la valeur de chaque chiffre des nombres suivants.
Question 1
Un élément BCcampus a été exclu de cette version du texte. Vous pouvez le consulter en ligne ici : https://opentextbc.ca/mathfortrades1/?p=83
Question 2
Un élément BCcampus a été exclu de cette version du texte. Vous pouvez le consulter en ligne ici : https://opentextbc.ca/mathfortrades1/?p=83
2
2
Ajout de nombres entiers
Harpreet et Jamieson effectuent actuellement un travail qui nécessite l’installation de sept toilettes dans un secteur du bâtiment et de six toilettes dans un autre. Au total, ils doivent installer 13 toilettes.
Ce n’est peut-être pas trop difficile à faire dans un calcul mental, mais que se passera-t-il si nous devons ajouter des chiffres plus importants? Par exemple, il y a 53 toilettes et 34 éviers de cuisine pour un travail qui fait l’objet d’un appel d’offres. C’est peut-être plus difficile à calculer mentalement.
Une façon facile d’additionner est d’utiliser une calculatrice, et si c’était le cas, nous obtiendrions une réponse de 87. Mais apprendre à additionner ces deux nombres entiers à l’aide des principes mathématiques peut nous aider non seulement à additionner les chiffres, mais aussi à visualiser comment ces chiffres vont ensemble.
Revenons au système de valeur de la position pour nous aider :
Premièrement, il y a 53, qui compte 5 dizaines et 3 unités.
Ensuite, regardez 34, qui compte trois dizaines et quatre unités.
Additionnez les dizaines : 5 dizaines + 3 dizaines = 8 dizaines.
Additionnez les unités : 3 unités + 4 unités = 7 unités.
Lorsque nous mettons les chiffres originaux dans le système de valeur de la position et que nous les additionnons, nous obtenons un total de 87. Séparer ce nombre dans chacun de ses chiffres et les positionner dans le système de valeurs de la position peut nous aider à visualiser la valeur de chacun des chiffres.
Suivez les étapes ci-dessous pour voir à quoi ressemble ce processus sur le plan mathématique.
Nous utiliserons les mêmes nombres que dans l’exemple précédent :
Étape 1 : Changez la question en formule facile à utiliser.
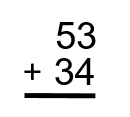Étape 2 : Additionnez les unités. Dans ce cas-ci, nous avons un 3 et un 4. Ensemble, ils totalisent 7.
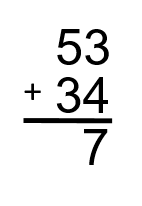Étape 3 : Additionnez les dizaines. Dans ce cas-ci, nous avons un 5 et un 3. Ensemble, ils totalisent 8.
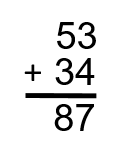
Cet exemple a bien fonctionné, car ni les unités ni les dizaines n’ont donné plus de 9. Et si c’était le cas? Jetez un coup d’œil à l’exemple suivant pour voir comment cela fonctionne.
Le mot « somme » est un langage mathématique pour additionner des chiffres. Lorsque nous disons : « Quelle est la somme de 27 et 45? », nous disons : « Quel est le total de ces chiffres si nous les additionnons? »
;
Trouvez la somme de 27 et 45.
Pour obtenir la somme de ces nombres, nous allons revenir à nos trois étapes.
Étape 1 : Changez la question en formule facile à utiliser.
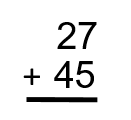
Étape 2 : Additionnez les unités. Dans ce cas-ci, nous avons un 7 et un 5. Ensemble, ils totalisent 12. C’est là que nous faisons ce qu’on appelle « reporter ». Regardez l’image suivante pour le voir en action :
Remarque : Dans ce cas-ci, on ne met pas le nombre 12 au bas de l’équation. Au lieu de cela, nous « reportons » le chiffre à la position suivante (les dizaines) dans le système de valeurs de la position.
Étape 3 : Additionnez les dizaines. Dans ce cas-ci, nous avons un 2 et un 4. Ensemble, ils totalisent 6. Il faut aussi tenir compte de l’unité que nous avons reporté. Nous l’ajoutons également pour obtenir un total de 7 à la position des dizaines.
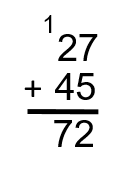
Remarque : S’il s’avérait que les dizaines totalisaient plus de 9, nous pourrions reporter l’unité dans la colonne des centaines. Jetez un coup d’œil ci-dessous pour voir comment cela fonctionne.
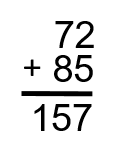
Comme il n’y a pas d’autres valeurs dans la colonne des centaines dans cette question, nous allons simplement placer celle-ci dans la colonne des centaines.
Essayez de vous exercer avec quelques questions et vérifiez les réponses dans la vidéo pour voir comment vous vous en êtes tiré. Assurez-vous de suivre les étapes décrites ci-dessus et de réfléchir à la valeur de la position de chacun des chiffres.
Un élément BCcampus a été exclu de cette version du texte. Vous pouvez le consulter en ligne ici : https://opentextbc.ca/mathfortrades1/?p=97
Un élément BCcampus a été exclu de cette version du texte. Vous pouvez le consulter en ligne ici : https://opentextbc.ca/mathfortrades1/?p=97
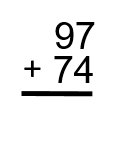
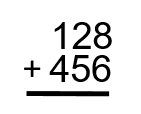
3
3
Soustraire des nombres entiers
À mesure que son entreprise prend de l’expansion, Harpreet demande à Jamieson de soumissionner pour plus de travaux. Harpreet a dû embaucher quelques plombiers pour l’aider à faire le travail, car les choses vont bien pour l’entreprise et les profits augmentent. Les choses vont si bien qu’ils ont dû refuser certains des travaux pour lesquels ils ont soumissionné (et obtenu). En fait, le mois dernier, ils ont soumissionné pour 17 travaux et ils les ont tous obtenus. Ils ne pensaient pas qu’ils gagneraient les 17 travaux et ils ont dû en refuser 5, alors il en restait 12. Voici un exemple de soustraction de nombres entiers.
La clé pour soustraire des nombres entiers est de trouver la différence entre les deux nombres. Si nous commençons avec 17 travaux et que Harpreet en a refusé 5, il en aurait accepté 12. Nous pourrions aussi considérer que cinq est la différence entre le nombre de travaux qu’il a obtenus et le nombre qu’il a pris. Nous pourrions formuler cette question de la façon suivante :
Nous utiliserons la première version écrite comme exemple, puis nous la transformerons en une autre version plus facile à utiliser.
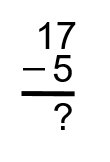
Vous remarquerez peut-être que la formulation de la question est semblable à la façon dont nous avons travaillé l’équation lorsque nous avons ajouté des nombres entiers. Cette façon de l’écrire nous donne une meilleure représentation des colonnes des unités et des dizaines, que nous devrons utiliser lorsque nous traiterons de la question.
La soustraction, comme l’addition, nous oblige à examiner chacune des colonnes une par une jusqu’à ce que nous atteignions notre réponse finale. Nous allons répondre à cette question de façon visuelle pour avoir une idée générale.
Commencez par 7 pommes dans la colonne des unités.
Enlevez (ou soustrayez) 5 de ces pommes, et il vous reste 2 pommes.
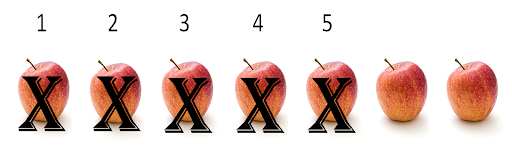
Cela règle la question de la colonne des unités. Nous avons commencé avec 7 pommes, puis nous avons soustrait 5 pommes, ce qui nous laisse 2 pommes dans la colonne des unités. Nous dirions que 2 est la différence entre 7 et 5.
Passons maintenant à la colonne des dizaines.
Il est intéressant de noter qu’il n’y a qu’un seul chiffre dans la colonne des dizaines, et il se trouve que c’est le chiffre 1. Cela facilite les choses, car il n’y a pas de travail à faire. Nous plaçons simplement le chiffre 1 dans la colonne des dizaines de la réponse, puis nous avons notre réponse finale.
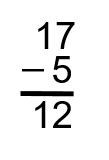
D’accord, c’était assez simple. Nous allons maintenant essayer quelque chose d’un peu plus difficile.
Imaginez que les choses se sont déroulées différemment pour Harpreet et Jamieson. Disons que, sur les 17 travaux pour lesquels ils ont soumissionné avec succès, ils ont dû en refuser 9. Combien de ces travaux auraient-ils effectué? Avant de continuer à lire et de voir la réponse, essayez de visualiser ce à quoi cela ressemblerait lorsque nous inscrirons ces chiffres dans la formule. Voyez-vous le problème?
Si nous commencions par la colonne des unités, comme nous l’avons fait dans le dernier exemple, le problème se poserait immédiatement. Le problème, c’est que si vous essayez de soustraire 9 de 7, vous vous retrouverez en négatif. Nous devons donc trouver une façon de soustraire ces chiffres.
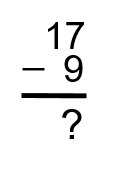
En fin de compte, nous empruntons un chiffre à partir de la colonne des dizaines. Nous nous retrouverions avec quelque chose qui ressemblerait à ceci :
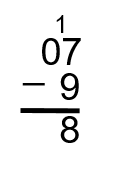
Lorsqu’on emprunte à partir de la colonne des dizaines, on emprunte une valeur de 10 et on l’ajoute à la colonne des unités pour aider les unités. Nous nous retrouvons avec 17 dans la colonne des unités, ce qui est maintenant plus que suffisant pour traiter le 9 à soustraire. De plus, peu importe la valeur que nous avions dans la colonne des dizaines (dans ce cas, il s’agissait d’un 1), elle est réduite de 1 pour tenir compte du fait qu’une dizaine a été empruntée.
Nous allons passer en revue un autre exemple dans lequel nous revenons à nos plombiers, Harpreet et Jamieson. Ils ont embauché trois employés, soit Dixon, Kavanir et Arman, et c’est une bonne chose. Les 17 travaux pour lesquels ils ont soumissionné au départ comprenaient l’installation de 246 appareils, notamment des baignoires, des toilettes et des éviers. Harpreet et Jamieson ne pouvaient pas faire tout ce travail par eux-mêmes.
Mais comme ils ont refusé cinq emplois, ils n’auront pas besoin d’installer 75 de ces appareils. Donc, avec l’aide des trois nouveaux employés, ils devraient être en mesure de terminer tous les travaux. La question est la suivante : « Combien d’appareils devront-ils installer? »
Comme d’habitude, commencez par la formule mathématique qui nous permet de bien répondre à la question. Mais cette fois-ci, nous allons suivre le processus par étapes, de sorte que lorsque vous regarderez en arrière, vous verrez comment ventiler les étapes.
Vous avez peut-être remarqué dans les deux premières sections que nous donnons souvent des exemples par étapes. Cela permet de diviser une grande question en parties faciles à gérer. Si vous suivez cette idée lorsque vous avez des problèmes de mathématiques, cela peut vous aider à rester sur la bonne voie.
D’accord, revenons au problème :
Étape 1 : Présentez la question dans un format facile à utiliser.
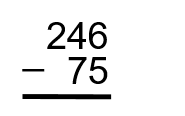
Étape 2 : Soustraire les unités. Dans ce cas-ci, nous avons 6 moins 5, ce qui donne 1.
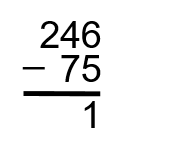
Étape 3 : Soustraire les dizaines. Ici, nous avons le problème suivant : le chiffre en haut (4) est inférieur au chiffre en bas (7), alors nous devons emprunter aux centaines. Le 2 dans la colonne des centaines doit être réduit à 1, puis l’autre 1 s’ajoute aux dizaines. Nous nous retrouvons avec 14 moins 7, ce qui donne 7.
Étape 4 : Soustraire les centaines. Dans ce cas-ci, nous n’avons que le 1, donc 1 moins 0 est 1.
Essayez quelques exemples de questions vous-même et vérifiez les réponses de la vidéo pour voir comment vous vous en êtes tiré.
Un élément BCcampus a été exclu de cette version du texte. Vous pouvez le consulter en ligne ici : https://opentextbc.ca/mathfortrades1/?p=117
Un élément BCcampus a été exclu de cette version du texte. Vous pouvez le consulter en ligne ici : https://opentextbc.ca/mathfortrades1/?p=117
4
Multiplication des nombres entiers
Au fur et à mesure que l’entreprise de Harpreet grandit, il doit acheter des fourgonnettes utilitaires pour lui-même et ses employés. Il est en mesure d’obtenir un contrat et d’acheter 4 fourgonnettes. Chacune de ces camionnettes doit être équipée d’outils, donc il commence par des clés. Il décide que chaque fourgonnette a besoin de 5 clés. Combien de clés y aura-t-il au total?
C’est un exemple de multiplication de nombres entiers. La façon dont nous pourrions exprimer ou écrire la multiplication est la suivante :
Quatre fois cinq OU 4 x 5
Si nous l’examinons d’un point de vue plus visuel, cela ressemblerait à ceci :
Dans ce cas, nous pouvions physiquement compter toutes les clés, et nous nous retrouvions avec 20. Nous pourrions également compter chaque rangée de 5 et les ajouter comme suit :
5 + 5 + 5 + 5 = 20
Ou nous pourrions prendre une ligne de 5 et la multiplier 4 fois parce qu’il y a 4 lignes. L’équation serait la suivante :
4 x 5 = 20
Chaque méthode devrait nous donner la même réponse, mais faire 4 fois 5 nous amène à la réponse plus rapidement. Si nous multiplions des nombres plus grands comme 8 temps 9 (8 × 9), nous pourrions passer beaucoup de temps à compter les clés ou à ajouter des nombres. La multiplication simplifie le processus.
Avant de multiplier les nombres plus grands, pourquoi ne pas passer par un autre exemple de multiplication des nombres plus petits et utiliser des éléments visuels pour nous aider avec notre réponse.
Exemple
Harpreet décide d’acheter des tournevis pour la fourgonnette et décide que chaque fourgonnette a besoin de 7 tournevis. Il décide également d’acheter 2 ensembles supplémentaires pour l’atelier. Au total, il décide d’acheter 6 ensembles de tournevis.
La première chose que nous devrions faire est d’écrire la question sous une forme avec laquelle nous pouvons travailler.
6 x 7 =
nombre d’ensembles de tournevis x nombre de tournevis dans chaque ensemble =
N’oubliez pas que vous pouvez aussi penser comme ceci :
7 + 7 + 7 + 7 + 7 + 7 =
Et encore une fois, nous pourrions les regarder visuellement et compter les tournevis.
Si nous les comptions, nous verrions que nous avons 42 tournevis. Si nous prenons notre calculatrice et entrons 6 fois 7, nous obtenons la même réponse. Si nous ajoutons 7 plus 7 plus 7 et ainsi de suite, nous obtenons aussi 42.
Maintenant, nous ne voulons pas avoir à passer à travers tout ce travail de comptage des tournevis chaque fois que nous multiplions de petits nombres ensemble. Ce que les élèves finissent par faire, c’est utiliser leur calculatrice ou simplement mémoriser leurs « tables de multiplication ». Les tables de multiplication sont une liste de nombres multipliés, commençant par 1 fois 1 et allant jusqu’à 12 fois 12. Jetez un coup d’œil à la photo à gauche pour avoir une idée de ce dont je parle ici. L’idée est que vous mémorisez ces tables de multiplication de sorte que lorsque vous voyez de petits nombres se multiplier, vous pouvez simplement accéder à votre mémoire pour la réponse.
Bien que la mémorisation de vos tables de multiplication est excellente pour les petits nombres, vous allez quand même rencontrer la multiplication de plus grands nombres. L’explication suivante passe en revue la façon dont nous abordons ce problème d’un point de vue mathématique.
Supposons que nous voulons multiplier de grands nombres ensemble. Comment pensez-vous que cela serait fait? La méthode suivante est utilisée pour calculer de grands nombres entiers, et nous allons passer directement à un exemple complet avec les étapes pour celui-ci comme étant tout le processus, et nous ne voulons vraiment pas passer par cela deux fois.
Quel est le produit de quatre cent trente-sept fois trois cent quatre-vingt-douze?
Le mot « produit » en mathématiques signifie la multiplication de deux nombres ensemble.
;
Une chose à garder à l’esprit, c’est que le processus que nous allons suivre ici prend un certain temps et représente beaucoup de travail. Si pendant le processus vous vous demandez, Serait-il plus facile d’utiliser une calculatrice?, vous auriez un bon cas. Mais le but de cet exercice est une fois de plus d’aider à comprendre comment les nombres vont ensemble. Rappelez-vous qu’une fois que vous aurez compris les bases des mathématiques, les concepts les plus difficiles seront traités plus facilement. Prendre le temps maintenant de bien comprendre le concept vous aidera à l’avenir et vous permettra également d’économiser de l’argent.
Étape 1 : Comme toujours, la première étape consiste à mettre la question dans un format facile à utiliser.
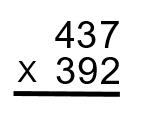
La procédure consiste généralement à simplement multiplier un groupe de plus petits nombres ensemble pour finalement obtenir le plus grand nombre. C’est là qu’il est vraiment utile de connaître vos tables de multiplication. Le nombre au bas de l’équation (dans ce cas, 392) sera utilisé et changera beaucoup plus que le nombre supérieur (437).
Étape 2 : Nous commençons le processus en agissant comme si nous ne faisions que multiplier le 437 par 2, le nombre dans la colonne des unités. Pensez-y comme à l’équation ci-dessous.
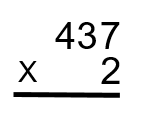
Comment cela fonctionne, c’est que vous allez d’abord prendre le 2 et le multiplier par le 7, puis le 2 sera multiplié par le 3, et finalement le 2 sera multiplié par le 4. Maintenant, tout cela ne se produit pas en une seule étape. Jetez un coup d’œil ci-dessous pour voir comment cela se fait.
Pour commencer, multipliez le 2 par le 7 pour obtenir 14 ; (2 × 7 = 14).
Entrez le 4 dans la colonne des « unités » et retenez le 1. Vous vous souvenez d’avoir retenu le 1? Étant donné que le nombre 14 est trop grand pour être placé dans la colonne des unités, nous devons prendre l’extra et le mettre dans le prochain calcul avec la colonne des dizaines.
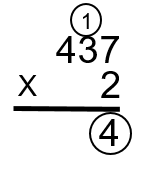
Étape 3 : Multipliez maintenant le 2 par le 3 pour obtenir le 6. Le 1 que nous venons de retenir est ensuite ajouté au 6 pour obtenir 7. Placez cette réponse dans la colonne des dizaines (2 × 3 + 1 = 7).
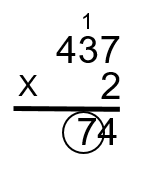
Étape 4 : Prenez le 2 et multipliez-le par le 4 pour obtenir le 8. Placez ce nombre dans la colonne des centaines (2 × 4 = 8).
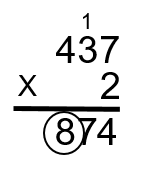
Remarque : 874 n’est pas la réponse finale. Nous avons encore quelques pas à réaliser. Une fois de plus, vous vous demandez peut-être si le fait d’utiliser une calculatrice serait plus facile, et vous avez raison. Ce serait beaucoup plus facile, mais travailler pour répondre à la question en utilisant cette méthode vous aidera à visualiser le processus derrière la multiplication.
Aussi, avant de passer à autre chose, prenez une seconde et revenez aux étapes initiales. Assurez-vous de comprendre le processus que nous venons de réaliser.
Étape 5 : La prochaine étape serait de faire la même chose avec le nombre dans la colonne des dizaines. Dans ce cas, le 9. Pensez-y comme en regardant l’équation comme celle ci-dessous.
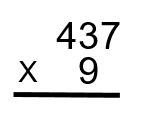
Notez l’espace vide à côté du 9. Lorsque nous commençons à prendre le 9 et à le multiplier par le nombre 437, cet espace vide dans la colonne des unités à côté du 9 doit être pris en compte. Pour ce faire, il faut placer un zéro pour commencer le processus et le placer dans la colonne des unités. Cela ressemblerait à quelque chose comme ce qui est montré ci-dessous.
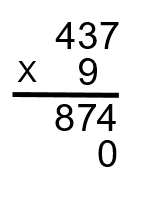
Étape 6 : Maintenant, allez-y et multipliez le 9 par les trois nombres dans la partie supérieure de l’équation, en commençant par le 7. Quand on prend le 9 et on le multiplie par le 7, on en obtient 63. Le 3 est placé dans la colonne des dizaines au-dessous du 7, puis retenez le 6 (9 × 7 = 63).
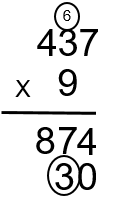
Étape 7 : Ensuite, multipliez ensuite le 9 par le 3 pour obtenir 27. Nous ajoutons ensuite le 6 qui a été retenu pour obtenir 33. Le 3 est placé dans la colonne des centaines sous le 8 et l’autre 3 est transporté dans la colonne des centaines à utiliser dans le prochain calcul(9 × 3 + 6 = 33).
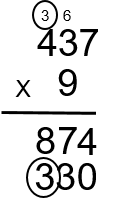
Étape 8 : Le 9 est ensuite multiplié par le 4 pour obtenir 36. Nous ajoutons ensuite le 3 qui a été retenu pour obtenir 39. Comme il s’agit du dernier calcul pour cette partie, mettez le 3 et le 9 dans la réponse. (9 × 4 + 3 = 39)
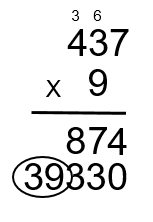
Maintenant, faites la même procédure en utilisant le 3 du nombre 392. Comme le chiffre 3 est tiré de la colonne des centaines, on peut y penser en regardant l’équation ci-dessous. Encore une fois, dans la réponse, nous devons tenir compte du fait que nous utilisons un chiffre dans la colonne des centaines et que nous ajoutons deux zéros dans la réponse pour commencer le processus.
Étape 9 : Prenez le 3 et multipliez-le par le 7 pour obtenir 21. Répétez la même procédure qu’avant (3 × 7 = 21).
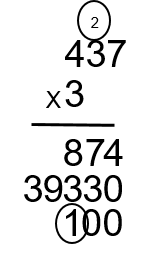Étape 10 : Maintenant prenez le 3 et multipliez-le par le 3 pour obtenir 9 et ajoutez le 2 retenu à partir de la première multiplication. Cela vous donnera 11 (3 × 3 + 2 = 11).
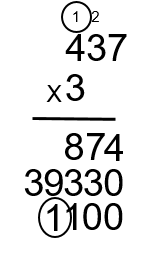Étape 11 : Prenez le 3 et multipliez-le par le 4 pour obtenir 12. Ajouter le 1 pour obtenir 13 (3 × 4 + 1 = 12).
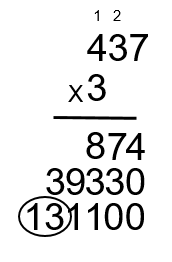
Étape 12 : ;Enfin, additionnez 874, 39 330 et 131 100 pour obtenir votre réponse finale.
Vous pourriez vouloir faire quelques choses à ce stade. L’une est de faire une pause et de se détendre. C’était beaucoup de travail à faire. Prenez une minute pour réaliser visuellement le processus dans votre esprit. Si vous avez le sentiment que vous avez besoin de le faire, repassez le travail en revue et assurez-vous de comprendre ce qui se passe.
La deuxième chose que vous pourriez vouloir faire à ce stade est de vérifier la réponse à l’aide d’une calculatrice. Entrez les chiffres et voyez ce que vous obtenez.
Essayez quelques exemples de questions vous-même, et vérifiez les réponses vidéo pour voir votre résultat. N’oubliez pas qu’il s’agit d’un long processus, alors prenez votre temps et portez attention aux détails.
Un élément BCcampus a été exclu de cette version du texte. Vous pouvez le consulter en ligne ici : https://opentextbc.ca/mathfortrades1/?p=141
Un élément BCcampus a été exclu de cette version du texte. Vous pouvez le consulter en ligne ici : https://opentextbc.ca/mathfortrades1/?p=141
5
Harpreet a fini avec un total de 12 travaux en production. Il a décidé d’embaucher 3 autres personnes pour l’aider avec tous les travaux. Ils sont Dixon, Kavanir et Arman. Il compte maintenant 4 employés, dont Jamieson et il répartit les travaux de façon égale entre les 4. Combien de travaux chacun d’entre eux fera-t-il?
Ce serait un exemple de division des nombres entiers. Harpreet a un total de 12 emplois et il a 4 employés qui divisent le nombre de travaux uniformément. Nous écrivons cette division comme ceci :
Comment pourrions-nous résoudre ce problème? Regardons-le visuellement pour commencer. Nous avons 12 travaux avec lesquels travailler.
Ce que nous faisons maintenant en divisant, c’est prendre le nombre que nous avons (12) et le diviser en nombre de groupes que nous allons avoir. Dans ce cas, nous avons 4 employés, nous allons donc les diviser en 4 groupes égaux.
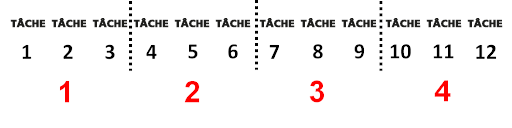
Vous pouvez maintenant compter qu’il y a 3 travaux dans chaque groupe. Ce que nous obtenons en fin de compte est :
Comme la multiplication, la division en petits nombres entiers est généralement assez directe. Mais que se passerait-il si nous avions un cas où nous avons un plus grand nombre. Comment feriez-vous ce calcul sans avoir recours à une calculatrice?
Ce que nous utilisons est un système appelé la « DIVISION NON ABRÉGÉE » qui ressemble à quelque chose comme ceci :
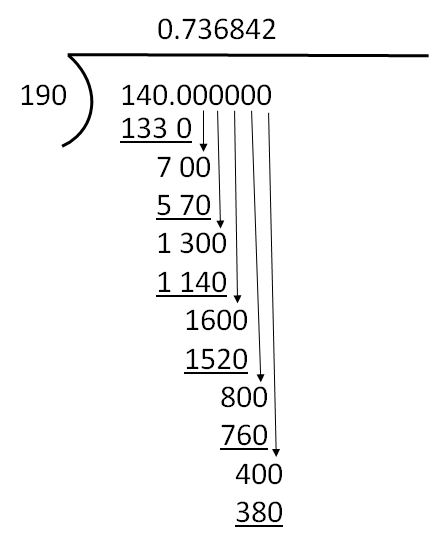
Nous utiliserons ce processus de division non abrégée pour répondre à la question suivante. Combien de fois 5 va-t-il dans 90?
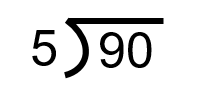
Remarque : le symbole situé à gauche sert à désigner une question de division non abrégée. Le placement des cinq dans l’équation indique que c’est le nombre à diviser par le 90. Essentiellement, l’équation est de demander combien de fois 5 peut aller dans 90.
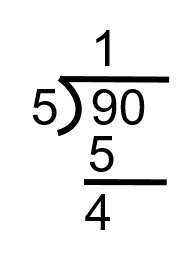
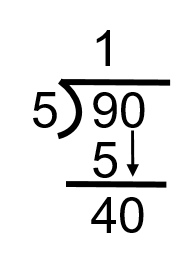
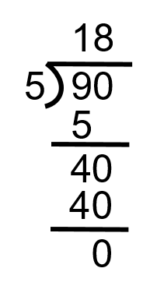
Puisque nous finissons avec zéro, il n’y a plus de chiffres avec lesquels travailler, ce qui signifie que nous avons fini.
Essayons un autre exemple.
Combien de fois 7 va-t-il dans 167?
Étape 1 : Configurez l’équation sous une forme utilisable.
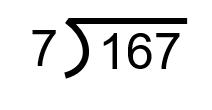
Étape 2 : Prenez le 7 et divisez-le dans le premier chiffre du nombre à diviser. Dans ce cas, c’est le 1, et nous pouvons voir que cela ne va pas fonctionner. Ainsi, nous ne faisons qu’avancer d’un pas vers la droite et divisons le 7 par 16.
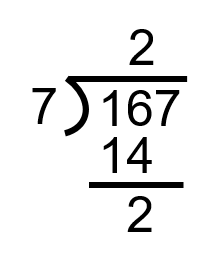
Pour terminer cette étape, nous devons faire descendre le prochain chiffre de l’équation. Dans ce cas, c’est le 7. Nous en avons maintenant 27 et l’étape suivante devient combien de fois 7 va dans 27.
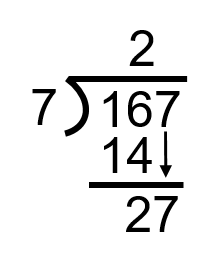
Étape 3 : Déterminez combien de fois 7 va dans 27 sans dépasser le nombre.
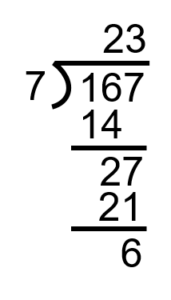
Nous nous retrouvons avec un scénario un peu différent ici que dans la première question. Quand nous arrivons à la fin de la question, il nous en reste 6. Ce que cela nous dit, c’est que 7 va dans 167 vingt-trois fois avec 6 restant.
Essayez quelques exemples de questions vous-même, et vérifiez les réponses vidéo pour voir votre résultat. N’oubliez pas de définir la question dans un format qui fonctionne.
Un élément BCcampus a été exclu de cette version du texte. Vous pouvez le consulter en ligne ici : https://opentextbc.ca/mathfortrades1/?p=155
Un élément BCcampus a été exclu de cette version du texte. Vous pouvez le consulter en ligne ici : https://opentextbc.ca/mathfortrades1/?p=155
6
6.
Un élément interactif H5P a été exclu de cette version du texte. Vous pouvez le consulter en ligne ici :
https://ecampusontario.pressbooks.pub/mathematiquesdemetier/?p=377#h5p-3
Si vous utilisez la copie papier, PDF ou de livre électronique de ce livre, accédez au lien ci-dessus pour réaliser le jeu-questionnaire. Cependant, les questions du jeu-questionnaire sont également fournies à l’Annexe C à la fin du livre pour une utilisation hors ligne.
II
Fractions
Résultats
· Distinguer et décrire différents types de fractions.
· Additionner et soustraire des fractions.
· Multipliez des fractions.
· Diviser des fractions.
7
Qu’est-ce qu’une fraction, de toute façon? Avez-vous déjà traité de fractions dans vos études ou dans votre travail? Une fraction est une partie (ou une portion) d’un tout. Disons que vous avez commandé une pizza et qu’il y avait un total de 8 tranches. Vous aviez faim ce jour-là et vous en aviez 5, mangeant donc 5 des 8 tranches. Cela peut être représenté comme une fraction.
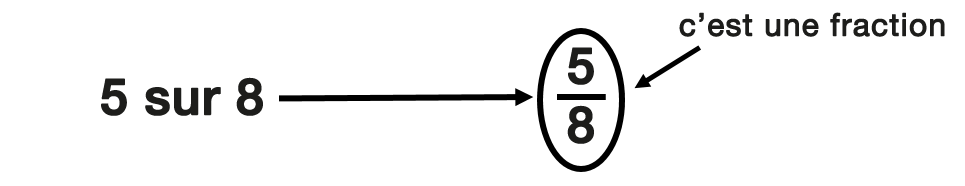
Notre histoire des fractions commence avec Abigail, Hanna, et Naomi, qui sont des apprenties électriciennes qui réalisent leur scolarité en même temps et qui espèrent ouvrir une entreprise ensemble une fois qu’ils auront leurs billets électriques du Sceau rouge.
Nous commencerons par quelques définitions. Chaque fraction comporte deux parties : le numérateur et le dénominateur. ; Jetons un coup d’œil à une fraction pour définir chacun.
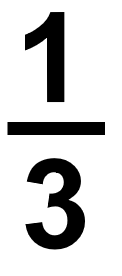
Numérateur : Le nombre au-dessus de la ligne dans une fraction. Il indique le nombre de parties du tout qui sont comptées.
Dénominateur : Le nombre sous la ligne dans une fraction. Il indique le nombre total de parties dans l’ensemble.
Si Abigail, Hanna et Naomi finissaient par posséder une entreprise, chacune en détiendrait ⅓. Chaque personne représente 1 propriétaire, et ensemble, il y a 3 propriétaires dans toute l’entreprise.
Voici quelques autres exemples de fractions :
Les exemples ci-dessus sont tous des fractions typiques, mais nous ne voyons pas toujours les fractions sous cette forme. Nous traitons de deux autres types de fractions : nombres mixtes et fractions impropres.
Disons que les trois apprenties se réunissent une nuit pour parler du futur, et elles commandent 2 pizzas, chacune avec 8 morceaux.
(Je sais que les pizzas ont l’air exactement les mêmes, mais vous devrez me faire confiance. Une chose est sûre, chaque pizza a 8 tranches, et quelqu’un est allé de l’avant et a réalisé un test de dégustation des deux pizzas.)
Nous devons décomposer cela : nous avons un total de 2 pizzas, chacune avec 8 tranches. Cela fait un total de 16 tranches. Si les apprenties mangent 1 pizza complète, ils auront mangé 8 tranches sur 8.
Maintenant, disons que l’une des trois prend une autre tranche de la deuxième pizza. Elles auront maintenant mangé 1 pizza entière plus 1 tranche.
nombre mixte
C’est ce qu’on appelle un nombre mixte. Un nombre mixte peut être défini comme suit :
Nombre mixte : Une combinaison d’un nombre entier et d’une fraction.
Ensuite, nous couvrons les fractions impropres.
Fraction impropre : Une fraction dans laquelle le numérateur est supérieur au dénominateur.
Cela signifie que le nombre sur le haut de la fraction est plus grand que le nombre sur le bas. Nous nous en tiendrons à notre exemple de pizza. Ensemble, les apprenties ont mangé un total de 9 tranches. Cela représente 1 pizza entière plus 1 tranche de la deuxième pizza. Écrit comme une fraction impropre, le nombre de pizzas mangées ressemblerait à ceci :
Maintenant, nous voulons changer un nombre mixte en une fraction impropre, puis faire l’inverse, prendre une fraction impropre et le changer en un nombre mixte.
Modifier le nombre mixte suivant en une fraction impropre :
Donc :
Voici une autre façon de trouver votre réponse :
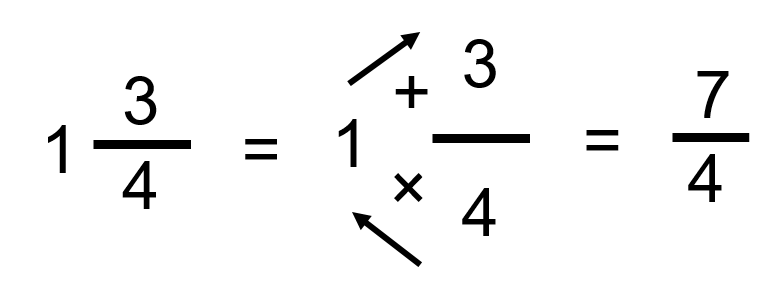
Cela peut paraître un peu déroutant, mais accompagnez-moi à travers l’équation. Avec le nombre mixte 1 ¾, prendre le 4 et le multiplier par le 1. Ajoutez 3, et vous obtenez 7. C’est la même réponse – juste une façon différente d’y arriver.
Essayez de passer d’un nombre mixte à une fraction impropre par vous-même.
Modifier le nombre suivant en une fraction impropre. Consultez la réponse vidéo pour voir comment vous avez fait.
Un élément BCcampus a été exclu de cette version du texte. Vous pouvez le consulter en ligne ici : https://opentextbc.ca/mathfortrades1/?p=45
Très bien : espérons que vous avez compris le calcul de nombre mixte à fraction impropre. Mais qu’en est-il de l’inverse? Nous devrions aussi passer en revue un exemple de cela, et ensuite vous donner la chance de le réaliser vous-même.
Modifier la fraction impropre suivante en un nombre mixte :
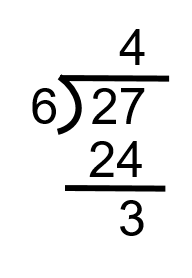
Essayez une autre question de pratique.
Modifier la fraction impropre suivante en un nombre mixte. Consultez la réponse vidéo pour voir comment vous avez fait.
Un élément BCcampus a été exclu de cette version du texte. Vous pouvez le consulter en ligne ici : https://opentextbc.ca/mathfortrades1/?p=45
Avant de passer à l’addition et à la soustraction des fractions, nous devrions aborder un autre concept appelé réduction des fractions. La réduction est ce que nous faisons quand nous voulons faire une version plus petite d’une fraction qui a toujours la même valeur mathématique que l’original.
Revenons à notre pizza. Encore une fois, nous avons 8 tranches par pizza. Maintenant, disons que nous mangeons 4 de ces tranches. Nous avons mangé :
Si quelqu’un vous demandait combien de pizza avez-vous mangé, comment répondriez-vous? Diriez-vous : « J’ai mangé 4 sur 8 tranches possibles », ou diriez-vous : « J’ai mangé la moitié de la pizza »? Je pense que nous sommes tous d’accord pour dire que nous avons mangé la moitié de la pizza, car 4 morceaux équivaudraient à la moitié de la pizza. Si nous écrivions la moitié en fraction, cela ressemblerait à ceci :
Nous pourrions alors conclure que les deux fractions représentent mathématiquement la même chose, et qu’elles ne sont que deux façons différentes de représenter la même chose. Vous pourriez le voir de cette façon : J’ai coupé deux morceaux de bois. L’un mesure 12 po de long, l’autre mesure 1 pied de long. Ils ont la même longueur – leurs longueurs sont simplement exprimées de différentes manières. Finalement, nous nous retrouvons avec ceci :
Nous avons réduit la fraction de 4 sur 8 à 1 sur 2 sans modifier la valeur réelle représentée. Comment cela a été fait mathématiquement, nous avons pris le numérateur d’origine de 4 et nous l’avons divisé par 4. Ce qui est fait à une partie de la fraction doit aussi être fait à l’autre, donc nous avons aussi divisé le dénominateur de 8 par 4, ce qui donne une fraction de 1 sur 2.
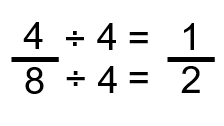
Le fait de faire la même chose au numérateur et au dénominateur garantit que la fraction originale et la fraction finale sont égales en valeur.
Nous réduisons les fractions lorsque nous pouvons diviser uniformément le même nombre pour le numérateur et le dénominateur. Dans notre exemple, 4 peuvent être divisés en deux. Notez que le nombre 2 peut aussi être divisé dans le numérateur et le dénominateur. Si nous divisons les deux par 2, nous obtiendrions :
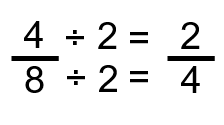
Bien que cela fonctionne encore mathématiquement, nous voulons souvent ramener une fraction à son expression la plus basse, ce qui signifie qu’elle ne peut plus être réduite. La fraction 2 sur 4 pourrait être réduite encore plus à 1 sur 2, donc il y a d’autres travaux que nous pourrions faire, si nous le voulions.
Passons en revue l’image mentale lors de la réduction des fractions. Prenez la fraction suivante et réduisez-la à son expression la plus basse :
Étape 1 : Ce que nous voulons faire ici, c’est jeter un coup d’œil à la fois au numérateur et au dénominateur et déterminer s’il y a un nombre qui peut entrer dans les deux. Il pourrait être plus facile si vous écrivez des nombres commençant par 1 et que vous décidez ensuite quels nombres peuvent aller à la fois dans 8 et 12.
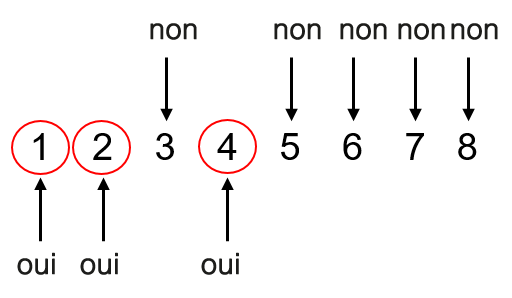
À partir de là, nous pouvons conclure que le plus grand nombre qui peut aller à la fois dans 8 et 12 est 4.
Étape 2 : Divisez le numérateur et le dénominateur par 4.
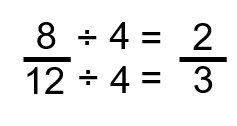
Voilà : la fraction est maintenant réduite à son expression la plus basse. Jetez toujours un coup d’œil à la réponse lorsque vous avez terminé, juste pour vous assurer qu’il n’y a certainement pas un autre nombre qui peut entrer dans le numérateur et le dénominateur, car cela signifierait que la fraction pourrait être réduite davantage.
L’exemple ci-dessus est assez simple. Une fois qu’il y a des nombres plus grands, il est parfois plus facile de résoudre la question en quelques étapes pour réduire lentement la fraction. Jetez un œil à l’exemple suivant pour voir ce que je veux dire.
Réduisez la fraction suivante à son expression la plus basse :
Étape 1 : Déterminez s’il y a un nombre qui peut aller dans le numérateur et le dénominateur. S’il y a plus d’un nombre, utilisez le plus grand nombre.
C’est un peu plus difficile que la première question, car les nombres sont beaucoup plus grands et plus difficiles à travailler avec eux. Revenons aux tables de multiplication, nous pouvons voir que 6, 8 et 12 vont tous dans 24. On pourrait aussi dire que 24 rentre dans 24. Mais qu’en est-il de 168? Quel nombre va dans cela?
Une chose que nous savons est que 2 va dans les deux, alors pourquoi ne pas commencer par prendre chaque partie de la fraction et la diviser par 2. Si vous avez du mal à diviser 168 par 2 dans votre tête, allez-y et utilisez votre calculatrice.
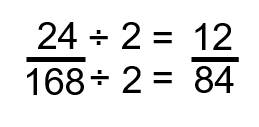
Étape 2 : Déterminer si la fraction peut être réduite davantage. Nous pouvons voir qu’une fois de plus, nous pouvons diviser les deux nombres par 2.
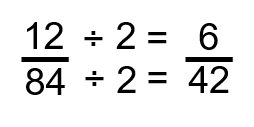
Étape 3 : Répéter l’étape 2 et déterminer si la fraction peut être réduite davantage. Ce que nous remarquons cette fois-ci, c’est que 6 peut aller dans 6 et 42, donc nous divisons le numérateur et le dénominateur par 6.
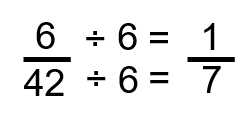
Voilà : nous avons réduit cette grande fraction à son expression la plus basse en quelques étapes. J’admets que si nous avions utilisé une calculatrice pour toute cette procédure, nous aurions pu trouver la réponse avec moins de travail, mais ce n’est pas le but. Le faire de la manière longue commence à entraîner votre cerveau dans les relations entre les nombres. En vous familiarisant davantage avec les nombres, vous serez en mesure de distinguer les structures et de comprendre les relations formées en mathématique. Bien que cela puisse prendre un peu plus de temps au début, le gain au fil du temps est immense.
Essayez quelques questions pour vous-même et vérifiez les réponses vidéo pour voir votre résultat.
Réduisez les fractions suivantes à leur expression la plus basse.
Un élément BCcampus a été exclu de cette version du texte. Vous pouvez le consulter en ligne ici : https://opentextbc.ca/mathfortrades1/?p=45
Un élément BCcampus a été exclu de cette version du texte. Vous pouvez le consulter en ligne ici : https://opentextbc.ca/mathfortrades1/?p=45
8
L’équation suivante est un exemple de multiplication de fractions. À première vue, cela peut sembler plus difficile que d’ajouter ou de soustraire des fractions, mais en réalité, c’est beaucoup plus facile. Ce qui pourrait être plus difficile à comprendre est la réponse que vous obtenez quand vous multipliez les fractions.
Nous allons jeter un coup d’œil à ceci visuellement, en utilisant un cercle découpé en parties pour régler cela. Pour commencer, nous allons diviser le cercle en 4 parties égales. Une de ces parties équivaudrait au quart du cercle.
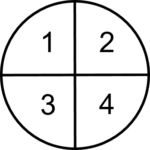
Si nous multipliions ce ¼ par ½, ce que nous faisions mathématiquement, c’est prendre ½ de la pièce de ¼, ou essentiellement diviser ce ¼ en deux parties égales. Cela finirait par représenter le ⅛ du cercle.
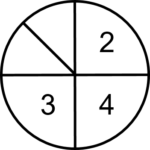
Mathématiquement, cela se fait de cette façon :
Multipliez les numérateurs ensemble
1 x 1 = 1
ET
Multipliez les dénominateurs ensemble
2 x 4 = 8
Nous en arrivons à :
Revenons à Abigail, Hanna et Naomi. Ils ont maintenant terminé un autre niveau de leurs études et arrivent à la fin de leur apprentissage. Tous trois travaillent sur le même travail, qui est un bâtiment de trois étages à ossature de bois, et chacune est responsable de l’installation brute de 30 bureaux. Elles sont tenues de câbler ⅙ de ces bureaux toutes les semaines. Une semaine, Hanna a dû manquer deux jours. Par conséquent, elle n’a travaillé que 3 jours sur 5, ou ⅗ du temps. Quelle fraction de bureaux aurait-elle pu mettre en place les câbles cette semaine-là, en tenant compte de son absence?
Commencez par noter les fractions avec lesquelles nous allons travailler dans cette situation.
le nombre de bureaux qui doivent être terminé au cours d’une semaine de 5 jours.
la fraction du temps travaillé pendant la semaine, 3 des 5 jours.
Ensuite, multipliez les deux fractions ensemble, en nous utilisant notre formule de multiplication des numérateurs ensemble, puis en multipliant les dénominateurs ensemble.
numérateurs (ligne du haut), dénominateurs (ligne du bas)
La réponse est donc :
Laquelle qui peut ensuite être réduite à son expression la plus basse :
Voici un autre exemple. Passons en revue les étapes de celle-ci.
Étape 1 : Multipliez les numérateurs ensemble.
Étape 2 : Multipliez les dénominateurs ensemble.
Étape 3 : Placez chacune des réponses à la place appropriée dans la fraction.
Étape 4 : Mettez la réponse à son expression la plus basse, si nécessaire, et changez-la en nombre mixte, si nécessaire. Dans cette question, nous sommes bons sur les deux plans.
Jusqu’à maintenant, vous avez peut-être pensé que vous avez compris cela et que c’est facile, mais maintenant, augmentons un peu le niveau de difficulté.
Avant de commencer, voyez-vous un problème? Le problème est que vous essayez maintenant de multiplier deux nombres mixtes ensemble. Comment cela fonctionne? Pouvez-vous simplement aller de l’avant et essayer de les multiplier tel qu’ils sont? La réponse est NON, mais la solution au problème n’est pas si difficile : il suffit de faire une étape de plus avant de passer par le processus.
La première chose à faire est de changer chacun des nombres mixtes en fractions impropres. À partir de là, le processus est le même.
Étape 1 : Changez chacun des nombres mixtes en fractions impropres. C’est la seule façon de répondre à cette question. Vous ne pouvez pas multiplier les nombres dans l’état où ils se trouvent.
Étape 2 : Multipliez les numérateurs ensemble.
Étape 3 : Multipliez les dénominateurs ensemble.
Étape 4 : Placez chacune des réponses à la place appropriée dans la fraction.
Étape 5 : Mettez la réponse à son expression la plus basse, si nécessaire, et changez-la en nombre mixte, si nécessaire. Dans ce cas, nous devons faire les deux. Nous commencerons par mettre la fraction à son expression la plus basse.
Alors, prenez cela et mettez-le dans un nombre mixte.
Essayez quelques questions vous-même. Assurez-vous d’inscrire votre réponse dans son expression la plus basse et, si nécessaire, de la transformer en un nombre mixte. Consultez les réponses vidéo lorsque vous avez terminé pour voir si vous êtes sur la bonne voie.
Un élément BCcampus a été exclu de cette version du texte. Vous pouvez le consulter en ligne ici : https://opentextbc.ca/mathfortrades1/?p=63
Un élément BCcampus a été exclu de cette version du texte. Vous pouvez le consulter en ligne ici : https://opentextbc.ca/mathfortrades1/?p=63
Un élément BCcampus a été exclu de cette version du texte. Vous pouvez le consulter en ligne ici : https://opentextbc.ca/mathfortrades1/?p=63
Un élément BCcampus a été exclu de cette version du texte. Vous pouvez le consulter en ligne ici : https://opentextbc.ca/mathfortrades1/?p=63
9
Abigail, Hanna et Naomi étudient pour leur examen de mi-session. Le matériel qu’elles doivent étudier comprend 16 chapitres de lecture. Les trois d’entre elles réalisent que 16 chapitres sont beaucoup de lecture pour chacune d’elles, alors elles décident d’étudier de manière plus efficace. Elles élaborent un plan dans lequel chacune d’elles lit un certain nombre de chapitres et le résume ensuite pour les deux autres. Elles partageront des notes, et chacune trouvera des vidéos en ligne correspondant à leur ensemble particulier de chapitres.
Par contre, les chapitres ne sont pas créés de façon égale. Certains sont plutôt faciles, tandis que d’autres sont beaucoup plus difficiles. Leur but est de répartir la charge de travail de façon égale entre les trois. Rappelez-vous qu’il y a 16 chapitres.
Abigail a le plus grand nombre de chapitres à lire avec 6. Hanna en a 5, et Naomi en a seulement 4. Si vous les additionnez, vous remarquerez qu’il ne s’agit que de 15 chapitres. Le dernier chapitre de l’ouvrage porte sur le dépannage des systèmes électriques, et les apprenties décident qu’elles liront celui-ci ensemble.
Nous pouvons représenter chacune de leurs charges de travail en une fraction de l’ensemble :
Abigail a 
Hanna a 
Naomi a
Et si on ajoutait ces fractions? Cela ressemblerait à ceci :
Vous remarquerez que les numérateurs sont tous différents, alors que les dénominateurs sont tous les mêmes (16). Lorsque vous ajoutez ou soustrayez des fractions, les dénominateurs doivent être les mêmes. Nous appelons cela un dénominateur commun.
Donc, pour obtenir la réponse à la question ci-dessus, vous n’avez qu’à ajouter tous les numérateurs. L’addition des fractions est très simple à cet égard.
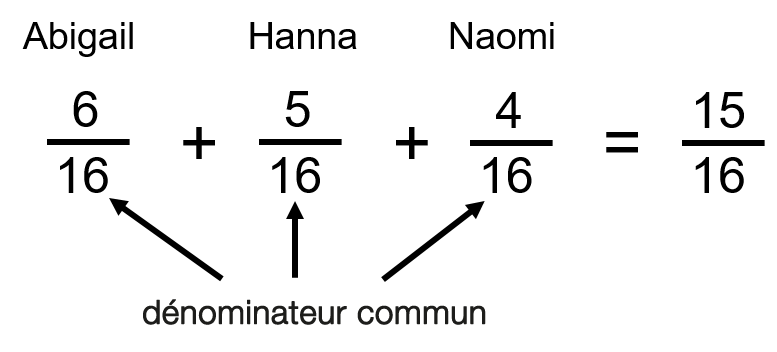
Notez que le dénominateur dans la réponse finale est le même que celui des fractions ajoutées. D’ici la fin, les apprenties auront examiné 15 des 16 chapitres séparément, puis elles liront le dernier chapitre ensemble.
Le concept d’addition de fractions avec des dénominateurs communs est assez facile, et nous avons assez fait pour ajouter des nombres entiers que passer en revue des exemples à ce stade pourrait ne pas en valoir la peine (mais si vous avez besoin d’une révision, voir Addition de nombres entiers). Ce que nous allons plutôt faire, c’est d’écrire quelques exemples d’addition de fractions pour que vous puissiez voir l’idée.
Remarquez-vous quoi que ce soit à propos de la réponse à la dernière équation? Elle peut être réduite.
Avant d’aller plus loin dans le travail sur les fractions, il serait peut-être bon de dire que, lorsqu’on travaille avec les fractions, on veut généralement mettre la réponse à son expression la plus basse.
Qu’en est-il de la soustraction des fractions? Elle suit le même principe : vous devez avoir un dénominateur commun, et ensuite vous soustrayez les numérateurs. Voici quelques exemples de soustraction des fractions :
Nous allons intensifier un peu maintenant. Nos exemples d’addition et de soustraction de fractions sont assez simples, car les dénominateurs sont les mêmes. Une situation plus difficile consiste à ajouter ou à soustraire des fractions qui ont des dénominateurs différents. Jetez un œil à l’exemple suivant :
Nous ne pouvons pas simplement additionner les numérateurs et les dénominateurs, car cela ne fonctionnera tout simplement pas. Jetez un coup d’œil aux deux cercles ci-dessous. L’un est divisé en 2 parties et l’autre en 8 parties. Remarquez-vous quelque chose sur la taille des parties?
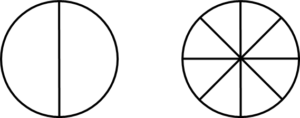
Vous remarquerez que les parties du cercle à 2 parties sont beaucoup plus grandes que celles du cercle à 8 parties. Si on additionnait les parties dans chaque cercle, ce serait comme ajouter des pommes et des oranges.
Donc l’idée devient de le faire de sorte que les parties que nous ajoutons soient de la même taille. Si nous pouvons en arriver à ce point, alors nous sommes prêts, et nous pouvons ajouter les deux fractions. C’est ce qu’on appelle la recherche d’un dénominateur commun, et le plus souvent, nous essayons de trouver le plus petit dénominateur commun.
Plus petit dénominateur commun : Le nombre le plus bas que les deux dénominateurs peuvent être égal.
Jetez un coup d’œil à l’équation ci-dessous. L’un des dénominateurs est 2, tandis que l’autre est 8.
Le processus ici est semblable à celui où nous avons placé les fractions à leur expression la plus basse dans la dernière section, seulement cette fois-ci, nous allons augmenter au moins un des dénominateurs, et parfois, nous allons augmenter les deux jusqu’à ce que nous en trouvions un qui est commun. Ce que nous cherchons, c’est un chiffre que les deux dénominateurs peuvent s’égaler. Dans cet exemple, nous voyons que 2 peut entrer dans 8 et 8 peut entrer dans 8. Cela nous laisse avec un dénominateur commun de 8.
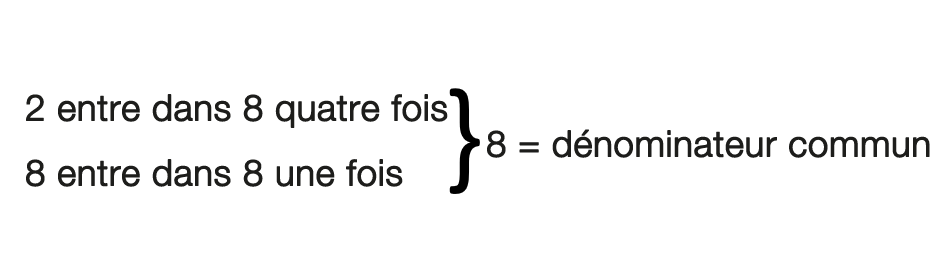
Nous avons déterminé que 8 sera notre dénominateur commun, ce qui signifie qu’une des fractions est déjà prête.
Mais qu’en est-il de 1 sur 2, ou la moitié? Nous devons transformer la moitié en une fraction avec 8 comme dénominateur.
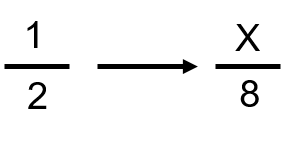
Comme nous l’avons calculé ci-dessus, 2 va dans 8 quatre fois.
C’est bon pour le dénominateur, mais qu’en est-il du numérateur? Quoi que nous fassions à une partie de la fraction, nous devons faire de même à l’autre partie. Cela laisse la fraction avec la même valeur. Nous devons ensuite multiplier le 1 par 4.
Si nous voulions tout faire en une seule étape, cela ressemblerait à ceci :
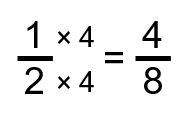
Nous avons maintenant quelque chose avec lequel nous pouvons travailler. Retournez à l’équation d’origine et remplacez le 1 sur 2 par 4 sur 8.
Bon, ça marche pour l’addition des fractions, mais qu’en est-il de la soustraction des fractions? La soustraction des fractions suit le même principe : si les dénominateurs ne sont pas les mêmes, alors nous devons trouver un dénominateur commun avant de soustraire les deux fractions.
Calculez les éléments suivants :
Étape 1 : Trouvez le dénominateur commun. Cela peut devenir un peu délicat quand les nombres commencent à grossir. À mesure que vous vous familiariserez avec les structures dans les nombres, les réponses seront plus faciles à trouver. La question que nous nous posons maintenant est : « Quel nombre peut entrer dans 8 et 16 pour qu’ils s’égalisent? »
On pourrait même commencer par voir si le plus petit dénominateur peut entrer dans le plus grand dénominateur. Dans ce cas, c’est le cas.
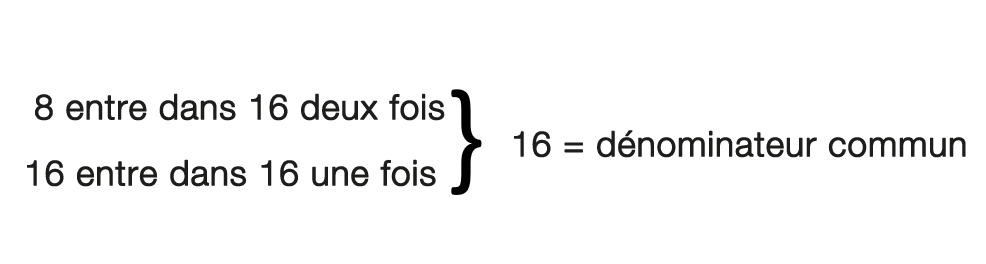
La fraction avec le dénominateur commun de 16 est déjà bonne, mais nous devons travailler avec la fraction avec un dénominateur de 8.
Étape 2 : Multiplier à la fois le numérateur et le dénominateur de ⅞ par 2 pour donner le dénominateur commun de 16.
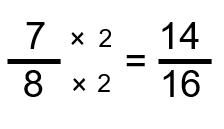
Étape 3 : Soustrayez les nouvelles versions des fractions.
Répondez aux questions pratiques suivantes et vérifiez les réponses vidéo. Assurez-vous d’inscrire chaque réponse dans son expression la plus faible ou en un nombre mixte, au besoin.
Un élément BCcampus a été exclu de cette version du texte. Vous pouvez le consulter en ligne ici : https://opentextbc.ca/mathfortrades1/?p=58
Un élément BCcampus a été exclu de cette version du texte. Vous pouvez le consulter en ligne ici : https://opentextbc.ca/mathfortrades1/?p=58
Un élément BCcampus a été exclu de cette version du texte. Vous pouvez le consulter en ligne ici : https://opentextbc.ca/mathfortrades1/?p=58
Un élément BCcampus a été exclu de cette version du texte. Vous pouvez le consulter en ligne ici : https://opentextbc.ca/mathfortrades1/?p=58
Attendez une minute! Cette dernière question est montée d’un cran en ajoutant des nombres mixtes. Je sais que vous avez déjà jeté un coup d’œil à la réponse vidéo, mais prenons un peu de recul et examinons les motions de l’addition et de la soustraction de nombres mixtes. Nous commencerons par une brève explication.
Le problème que nous rencontrons lors de l’ajout ou de la soustraction de nombres mixtes est qu’un nombre mixte est composé de deux parties distinctes : il y a le nombre entier, et puis il y a la fraction. Lors de l’addition des nombres, ceci peut être simple, comme l’équation suivante :
Plutôt simple, n’est-ce pas? Vous ajoutez simplement les deux nombres entiers, puis vous additionnez les fractions. Cela fonctionne assez bien. Mais qu’en est-il d’une situation comme l’exemple suivant?
Le problème (ce n’est pas vraiment un problème) est que, quand on ajoute les fractions, on obtient un plus grand nombre dans le numérateur que dans le dénominateur.
La solution est de changer la partie inappropriée de la réponse en un nombre mixte, puis de l’ajouter à la partie du nombre entier de la réponse.
Prenez le 7 et ajoutez-le au nombre mixte pour obtenir notre réponse finale.
Cela semblait assez simple, mais qu’en est-il de la soustraction? Nous suivons les mêmes règles. Jetez un œil à l’exemple suivant :
La procédure est similaire à celle pour additionner des fractions, mais au lieu d’additionner, nous soustrayons. Nous pouvons diviser l’équation en deux parties. Nous commençons par soustraire les nombres entiers, puis nous continuons en soustrayant la partie des fractions.
Étape 1 : Soustrayez les nombres entiers.
Étape 2 : Soustrayez la partie des fractions de l’équation.
Étape 3 : Rassemblez le tout ensemble.
Ce n’est pas trop difficile, n’est-ce pas? Mais jetez un coup d’œil à l’exemple suivant et voyez si vous pouvez comprendre le problème que nous allons avoir au fur et à mesure que nous l’effectuons.
Le problème n’apparaît pas quand on soustrait les nombres entiers, mais quand on soustrait les fractions.
Nous nous retrouverions avec une réponse inférieure à zéro. Cela ne va pas fonctionner pour nous. Alors comment résoudre le problème? La réponse réside dans l’emprunt, et ce que nous empruntons est le nombre entier, 5. Disons qu’on emprunte 1 de 5. Cela nous laisserait avec 4, et puis quoi? Jetez un coup d’œil à la logique suivante.
Si nous allons de l’avant et divisons les 5 en 4 et 1, et que nous divisons ce 1 en parties de 8, nous avons beaucoup plus de huit pour réaliser l’équation. Nous pouvons maintenant tout rassembler pour obtenir ce qui suit :
Nous avons maintenant des nombres avec lesquels nous pouvons travailler dans notre question initiale.
Nous suivons maintenant les mêmes étapes qu’avant.
Étape 1 : Soustrayez les nombres entiers.
Étape 2 : Soustrayez la partie des fractions de l’équation.
Étape 3 : Rassemblez le tout ensemble.
Ajoutez ou soustrayez les nombres mixtes suivants, en vous assurant de mettre votre réponse à l’expression la plus basse. Consultez les réponses à la vidéo à la fin pour voir votre résultat.
Un élément BCcampus a été exclu de cette version du texte. Vous pouvez le consulter en ligne ici : https://opentextbc.ca/mathfortrades1/?p=58
Un élément BCcampus a été exclu de cette version du texte. Vous pouvez le consulter en ligne ici : https://opentextbc.ca/mathfortrades1/?p=58
Un élément BCcampus a été exclu de cette version du texte. Vous pouvez le consulter en ligne ici : https://opentextbc.ca/mathfortrades1/?p=58
Un élément BCcampus a été exclu de cette version du texte. Vous pouvez le consulter en ligne ici : https://opentextbc.ca/mathfortrades1/?p=58
10
La division des fractions suit une logique similaire à la multiplication des fractions. Il s’agit de travailler séparément avec les numérateurs et les dénominateurs. Une fois que vous avez fait vos calculs initiaux, vous devez tout rassembler pour obtenir votre réponse. Il y a cependant un petit revirement que nous devrons examiner au fur et à mesure que nous aborderons certaines questions.
Avant d’aborder tout cela, commençons par revoir la division des nombres entiers, et ensuite nous allons travailler jusqu’aux fractions.
Commencez par 20 tournevis :
Divisez maintenant ces 20 tournevis par 10 (ou en groupes de 10).
Vous vous retrouvez avec 2 groupes de 10.
Divisez maintenant ces 20 tournevis par 5 (ou en groupes de 5).
Vous vous retrouvez avec 4 groupes de 5.
Divisez maintenant ces 20 tournevis par 2 (ou par groupes de 2).
Vous vous retrouvez avec 10 groupes de 2.
Regardez les mathématiques ici. Voyez-vous une tendance? Qu’avez-vous trouvé? Avez-vous remarqué que, lorsque vous prenez votre montant initial (dans ce cas, 20) et divisez-le par un nombre qui continue de diminuer (10, puis 5, puis 2), nous finissons avec une réponse qui devient plus grande.
Suivez cette logique dans les fractions, en gardant à l’esprit que les fractions ne sont pas seulement inférieures à 10, 5 et 2, mais aussi 1. En utilisant cette tendance, nous déterminons que diviser les 20 tournevis par un nombre inférieur à 1 nous donnerait une réponse plus grande que si nous divisions le 20 par 10, 5 ou 2.
Essayez ceci. Prenez les 20 tournevis, et divisez-les par ½. À votre avis, quelle sera votre réponse?
Selon notre logique, la réponse devrait être de plus de 10, et en fait, elle l’est.
Cela ne signifie pas que nous nous retrouvons avec 40 tournevis, cependant. Ça veut dire que nous nous retrouvons avec 40 parties de tournevis. Vous devez imaginer que chacun des tournevis a été divisé en 2. Vingt tournevis divisés en deux nous donneraient 40 pièces en fin de compte. La question qui se pose maintenant est : comment faire cela mathématiquement? La réponse est d’utiliser ce qu’on appelle la réciproque. Voici la définition.
Réciproque : Un nombre qui a une relation avec un autre nombre de façon que son produit est 1.
Cela signifie que, lorsque vous prenez un nombre tel que 5 et que vous le multipliez par sa réciproque, vous obtiendrez une réponse de 1. Nous commencerons par le chiffre 5. Nous pourrions aussi écrire le chiffre 5 sous forme de fraction.
En utilisant notre définition de réciproque, nous devons trouver un nombre qui, lorsqu’il est multiplié par 5/1, nous donne une réponse de 1.
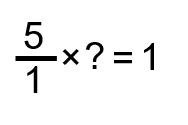
Pour trouver la réponse, nous devons revenir à la multiplication des fractions. Rappelez-vous que, quand nous multiplions les fractions, nous multiplions simplement les numérateurs ensemble et ensuite multiplions les dénominateurs ensemble. À partir de là, nous pouvons conclure que :
En fin de compte, pour trouver la réciproque d’une fraction, nous prenons simplement le numérateur et en faisons le dénominateur et prenons le dénominateur et en faisons le numérateur. Essentiellement, nous ne faisons qu’inverser la fraction. Voici d’autres exemples de réciproques.
ET 
Bon, maintenant que nous avons réglé la question des réciproques, la question devient alors : pourquoi avons-nous besoin de la réciproque en premier lieu? La réponse se trouve dans la règle pour diviser les fractions.
La règle pour diviser les fractions est de prendre la première fraction et de la multiplier par la réciproque de la seconde fraction. Oui, vous avez entendu : pour diviser, vous multipliez, mais seulement après avoir retourné la deuxième fraction.
En retournant la deuxième fraction (en trouvant sa réciproque), on modifie la valeur de l’équation. Pour que l’équation reste mathématiquement la même, nous devons changer la question de division en question de multiplication. Jetez un coup d’œil à l’exemple suivant pour voir comment cela se fait.
Exemple
Étape 1 : Mettez la question sous une forme avec laquelle vous pouvez travailler. Cela comprend de trouver la réciproque de la deuxième fraction puis de la multiplier par la première.
Nous en arrivons à :
La réciproque de 
est 
Vérifiez : 
Alors nous obtenons :
devient 
Étape 2 : Suivez la même procédure que lors de la multiplication des fractions. Multipliez les numérateurs ensemble, puis multipliez les dénominateurs ensemble.
Multipliez les numérateurs ensemble
Multipliez les dénominateurs ensemble
Étape 3 : Prenez ces réponses et remettez-les dans une fraction.
Étape 4 : Mettez la réponse à son expression la plus basse, puis en un nombre mixte, si nécessaire.
chiffres mixtes
Réponse finale :
Exemple
Étape 1 : Mettez la question sous une forme avec laquelle vous pouvez travailler. Cela comprend de trouver la réciproque de la deuxième fraction puis de la multiplier par la première.
devient 
Étape 2 : Multipliez les numérateurs ensemble, puis multipliez les dénominateurs ensemble.
Multipliez les numérateurs ensemble
Multipliez les dénominateurs ensemble
Étape 3 : Prenez ces réponses et remettez-les en une fraction.
Étape 4 : Mettez la réponse à son expression la plus basse, puis en un nombre mixte, si nécessaire. Dans ce cas, la réponse est à la fois à son expression la plus basse et est déjà une fraction adéquate, donc nous avons terminé.
Essayez ces questions pratiques et jetez un œil aux réponses vidéo pour voir votre résultat.
Un élément BCcampus a été exclu de cette version du texte. Vous pouvez le consulter en ligne ici : https://opentextbc.ca/mathfortrades1/?p=72
Remarque : Celui-ci est légèrement différent de ce que nous avons fait, car il s’agit de diviser des nombres mixtes. Que pensez-vous qu’il vous faudra faire lorsque vous réalisez cette question?
RÉPONSE : Vous devez d’abord changer le nombre mixte en une fraction impropre. Ensuite, vous pouvez résoudre la question de la même façon que nous l’avons fait auparavant.
Un élément BCcampus a été exclu de cette version du texte. Vous pouvez le consulter en ligne ici : https://opentextbc.ca/mathfortrades1/?p=72
11
Jeu-questionnaire sur les fractions
Un élément interactif H5P a été exclu de cette version du texte. Vous pouvez le consulter en ligne ici :
https://ecampusontario.pressbooks.pub/mathematiquesdemetier/?p=423#h5p-3
Si vous utilisez la copie papier, PDF ou de livre électronique de ce livre, accédez au lien ci-dessus pour réaliser le jeu-questionnaire. Cependant, les questions du jeu-questionnaire sont également fournies à l’Annexe C à la fin du livre pour une utilisation hors ligne.
III
Nombres décimaux
Objectifs
· Comprendre la notation décimale.
· Comparer et arrondir les nombres décimaux.
· Convertir des fractions en nombres décimaux.
· Convertir des nombres décimaux en fractions.
12
Passons en revue quelques exemples, juste pour nous assurer que nous sommes tous sur la même longueur d’onde.
Dans le nombre ci-dessous, indiquez le chiffre qui se trouve à la place des millièmes.
La façon la plus simple de le faire est d’écrire le nombre, puis, en commençant par la gauche, d’indiquer la valeur de place de chacun des chiffres.
Le 6 est à la place des millièmes.
Essayons un autre exemple.
Dans le nombre ci-dessous, indiquez le chiffre qui se trouve à la place des cent-millièmes.
Une fois de plus, pour trouver la réponse, notez le nombre, puis indiquez la valeur de la place de chacun des chiffres.
Le 1 est à la place des cent-millièmes.
13
Chad veut s’assurer que tous ses étudiants comprennent la valeur de l’argent, et un aspect important de cela est de savoir comment déterminer avec précision la taille des décimales. Jetez un coup d’œil aux quatre décimales suivantes.
Laquelle d’entre elles est la plus grande? Pour répondre à la question, il faudrait comparer les décimales.
À première vue, vous pourriez dire que le plus grand nombre est 8,151 38, car il a le plus de chiffres et peut sembler être le plus grand. Mais si nous revenons au chapitre sur Comprendre la notation décimale, nous nous souviendrons que, lorsque vous allez plus loin à droite à partir de la virgule (,), les chiffres deviennent plus petits. Ainsi, dans l’exemple 8,15138, le 3 près de la fin valent beaucoup moins que le 5 deux positions à la gauche de la virgule.
Si nous suivonscette logique, alors le plus grand nombre des quatre serait 8,16, même s’il a le moins de chiffres. Quand on compare les décimales, il faut vraiment commencer par le nombre entier. Dans cette situation, il est 8 pour les quatre réponses, donc il n’entre pas en jeu.
Une fois que nous avons décidé que le nombre entier est égal dans les quatre cas, la prochaine chose que nous devons examiner est le nombre directement à droite de la décimale. C’est la place des dixième et vaut le plus en décimales. Encore une fois, les quatre réponses nous donnent une valeur de 1 dans la colonne des dixièmes, donc ce ne sera pas le facteur déterminant. Déplacez encore d’un espace vers la droite et vous obtenez la place des centièmes. Tous les nombres contiennent un 5, sauf le premier, où nous avons un 6. Par conséquent, il s’agit de la valeur décisive de la place.
Je vais passer en revue un autre exemple, et ensuite vous pouvez essayer quelques questions tout seul.
Lequel des nombres suivants est le plus grand?
En suivant la même structure qu’avant, nous passerions par les étapes suivantes.
Étape 1 : Commencez par le nombre entier. Quel nombre a le plus grand nombre entier? Comme ils sont tous égaux, ce ne sera pas le facteur déterminant.
Étape 2 : Allez au premier chiffre à droite de la décimale. Il s’avère que le chiffre est 3 dans tous les cas. Par conséquent, ce n’est pas non plus le facteur décisif.
Étape 3 : Déplacez-vous à nouveau d’un espace à droite. Ce serait la place des centièmes. Ici, nous trouvons la première différence. La réponse A nous donne le plus grand nombre dans cette colonne. Par conséquent, la réponse A est le plus grand nombre.
Par conséquent, le plus grand nombre des quatre est :
Essayez maintenant quelques questions par vous-même et regardez les réponses vidéo.
Trouvez le plus grand nombre.
Un élément BCcampus a été exclu de cette version du texte. Vous pouvez le consulter en ligne ici : https://opentextbc.ca/mathfortrades1/?p=177
Un élément BCcampus a été exclu de cette version du texte. Vous pouvez le consulter en ligne ici : https://opentextbc.ca/mathfortrades1/?p=177
Au cours du cours, Chad parle de l’importance de l’argent et de la manière de travailler efficacement avec celle-ci, en particulier en matière de tenue des comptes. Assurez-vous de suivre les transactions commerciales jusqu’au centime (ou à la décimale). Comme nous avons 100 cents dans un dollar, si nous arrondissions les totaux comptables, nous arrondirions aux 10 cents les plus près (dixièmes) ou même au dollar le plus près (un dollar).
Avant d’arriver à l’arrondissement des décimales, nous devrions commencer par l’arrondissement en général. On demande aux étudiants de compter les raccords sur une table.
Il y a un total de 22 raccords sur la table, et on demande maintenant aux étudiants d’arrondir le nombre de raccords au 10 près. Cela signifierait arrondir à 10, 20, 30, 40, etc. Cet exemple peut sembler simple, puisque nous sommes beaucoup plus près de 20 qu’à 30, et si vous avez répondu 20, alors vous auriez raison. Mais quelle est la règle que nous suivons?
RÈGLE : Trouvez la valeur de place que nous arrondissons (dans ce cas, la position des dizaines). Regardez le chiffre à droite de ce numéro (dans ce cas, la place des unités). Si ce nombre est de 4 ou moins, nous arrondissons vers le bas. Si ce nombre est 5 ou plus, nous arrondissons vers le haut.
Dans notre exemple avec les 22 raccords, nous avons un 2 dans la colonne des unités, donc nous finissons par arrondir à 20. Si le nombre dans la colonne des unités était de 5 ou plus, nous arrondirions à 30.
Passons en revue quelques exemples avant de passer à autre chose.
Arrondir les nombres suivants au 10 le plus près. N’oubliez pas votre système de valeur de place ici.
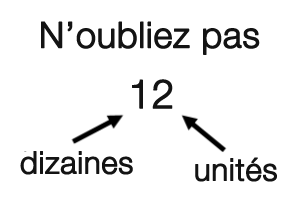
Vérifiez la réponse pour D. Lorsque nous arrondissons la colonne des dizaines, nous finissons par arrondir vers le haut. Nous n’avons plus de place dans la colonne des dizaines, car le nombre le plus élevé que nous puissions faire avec ce nombre est 90. Cela nous force à entrer dans la colonne des centaines et à commencer par 1, ce qui donne la réponse 100.
Maintenant que nous avons arrondi des nombres entiers complets, passons à l’arrondissement des décimales. L’arrondissement des décimales suit les mêmes principes. Il est important ici de se rappeler le système de valeur de place, non seulement pour les nombres entiers, mais aussi pour les décimales. Prenez note de la règle suivante lors du traitement des nombres :
Lorsque vous passez de droite à gauche dans un nombre, y compris les décimales, la valeur des chiffres devient plus grande. En ce qui concerne les décimales, ce principe signifie que, plus vous allez loin à droite de la décimale, plus vous traitez avec des portions de plus en plus petites d’un nombre entier.
Commençons par un exemple.
Arrondir le nombre suivant jusqu’au centième le plus près.
Étape 1 : Identifiez le chiffre dans la colonne des centièmes.
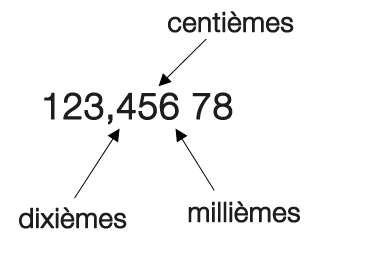
Étape 2 : Regardez le chiffre directement à droite de la colonne des centièmes. Dans ce cas, ce serait le chiffre dans la colonne des millièmes, qui est 6.
Étape 3 : Suivez les règles de l’arrondissement.
RÈGLE : Si le nombre est de 4 ou moins, arrondissez vers le bas. Si le nombre est égal ou supérieur à 5, arrondissez vers le haut.
Puisque nous en avons 6 dans la colonne des millièmes, nous arrondissons vers le haut.
Par conséquent, 123,456 7 arrondis au centième près est :
Arrondir les décimales suivantes. Assurez-vous de tenir compte du système de valeur de place lorsque vous répondez aux questions. Consultez les réponses vidéo pour voir votre résultat.
Arrondir au dixième près.
Un élément BCcampus a été exclu de cette version du texte. Vous pouvez le consulter en ligne ici : https://opentextbc.ca/mathfortrades1/?p=177
Arrondir au millième près.
Un élément BCcampus a été exclu de cette version du texte. Vous pouvez le consulter en ligne ici : https://opentextbc.ca/mathfortrades1/?p=177
Arrondir jusqu’au centième le plus près. C’est un nouveau concept. Avant de vérifier la réponse vidéo, essayez de résoudre ce problème et voyez si vous avez la bonne réponse.
Un élément BCcampus a été exclu de cette version du texte. Vous pouvez le consulter en ligne ici : https://opentextbc.ca/mathfortrades1/?p=177
14
Chad a décidé qu’il voulait travailler avec l’argent sous forme de fraction et non sous forme décimale. Pourquoi, demandez-vous? Je ne sais pas. Travaillez avec moi ici, cependant, parce qu’il a été difficile de faire entrer Chad dans l’histoire de la décimale. Peut-être veut-il juste que ses étudiants en sachent un peu plus sur les mathématiques. Il n’y a pas de problème ici. Voici ce que nous examinons :Il est important de savoir comment le faire afin de travailler avec différentes formes numériques en milieu de travail. Par exemple, David, un étudiant de la classe Chad, est un machiniste. Les machinistes produisent des pièces métalliques avec une précision allant jusqu’à un millième de pouce. Si vous travaillez continuellement en décimales, vous pourriez oublier comment travailler avec les fractions, alors David veut savoir comment changer ces décimales en fractions. La meilleure façon d’illustrer comment le faire est simplement d’avoir un exemple.
Nous commencerons par une décimale facile comme 0,25 et nous nous efforcerons de changer cela en une fraction.
Étape 1 : Mettez la question sous forme de fraction de sorte que la décimale soit supérieure à 1.
Étape 2 : Prenez le numérateur et le dénominateur et multipliez chacun par 10 pour chaque chiffre à droite de la virgule décimale. Dans ce cas, nous avons 2 chiffres à la droite. Par conséquent, nous multiplions chacun par 100 (10 × 10).
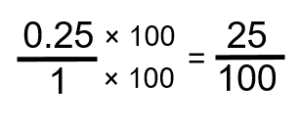
Étape 3 : Réduisez la fraction à son expression la plus basse, et nous obtenons la réponse finale.
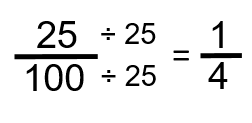
Changez la décimale 0,729 en une fraction.
Étape 1 : Mettez l’équation sous forme de fraction de sorte que la décimale soit supérieure à 1.
Étape 2 : Prenez le numérateur et le dénominateur et multipliez chacun par 10 pour chaque chiffre à droite de la virgule décimale. Dans ce cas, nous avons 3 chiffres à la droite. Par conséquent, nous multiplions chacun par 1000 (10 × 10 × 10).
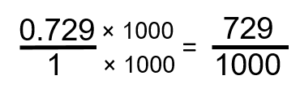
Étape 3 : Réduisez la fraction pour obtenir notre réponse finale.
C’est un nombre difficile à réduire. Ma suggestion serait de le faire par étapes. Commencez par de petits nombres comme 2 et 3. Est-ce que le chiffre 2 va à la fois dans le numérateur et le dénominateur? La réponse serait non. Et qu’en est-il de 3? Cela ne fonctionne pas non plus. Continuez ce processus jusqu’à ce que vous trouviez un numéro qui fonctionne.
Il est possible que vous ne trouviez pas un chiffre et que nous soyons déjà à l’expression la plus basse. C’est le cas ici. Notre dernière réponse est simplement :
Essayez quelques questions pratiques et vérifiez les réponses vidéo.
Changez les décimales suivantes en fractions. Mettez votre réponse à son expression la plus basse.
Un élément BCcampus a été exclu de cette version du texte. Vous pouvez le consulter en ligne ici : https://opentextbc.ca/mathfortrades1/?p=184
Un élément BCcampus a été exclu de cette version du texte. Vous pouvez le consulter en ligne ici : https://opentextbc.ca/mathfortrades1/?p=184
Maintenant, il est temps de passer à une situation que nous pourrions trouver en lieu de travail;. Avez-vous déjà été sur un lieu de travail, et votre patron vous a demandé de couper un morceau de tuyau, ou peut-être un morceau de bois? Quelle était la mesure? Peut-être que c’était à peu près 8 ⅜ pouces. Peut-être que c’était 2 pieds et 2 ¼ pouces. C’est plutôt standard.
Mais si on vous demandait de couper une pièce de 2,938 4 pieds? Pour David, le machiniste, c’est peut-être exactement le type de mesure qu’il obtiendrait en créant des produits métalliques. Mais que feriez-vous dans d’autres métiers?
C’est la raison pour laquelle nous devons être en mesure de changer les décimales en fractions. Le nombre entier dans cet exemple reste le même, donc nous n’avons pas vraiment besoin de traiter cela. Nous devons travailler avec le 0,9384.
L’objectif est de changer 2,938 4 en pieds, pouces et en fractions d’un pouce. Nous allons passer en revue un exemple pour vous montrer comment cela se fait.
Étape 1 : Tout d’abord, notez que le nombre dont nous parlons est en pieds. Nous avons 2,938 4 pieds. Les 2 pieds entiers ne nécessiteront aucun changement et ce nombre est bon comme il est. Ce que nous devons faire en premier, c’est de changer 0,938 4 en pouces avant de passer à des fractions d’un pouce. Commencez par le nombre de pouces qu’il y a dans un pied.
Prenez la décimale d’un pied et multipliez-la par 12.
Étape 2 : Il nous reste 11 pouces et les décimales d’un pouce. Le 11 pouces est bon comme il est, mais nous devons changer la décimale d’un pouce en fractions d’un pouce. La question devient : en quelle fraction d’un pouce devront-ils le changer?
C’est à vous de décider. Cela pourrait être en quatrièmes, en huitièmes, en seizièmes ou en trente-deuxièmes. La façon la plus courante serait de changer la décimale d’un pouce en seizièmes. Pour ce faire, on multiplie la décimale d’un pouce par le nombre dans le dénominateur de la fraction vers laquelle vous travaillez. Par exemple, nous cherchons à convertir la décimale en seizièmes, donc nous la multiplions par 16.
Quand nous regardons 4,172 8, ce que nous regardons en fait est :
Si nous avions pris le 0,260 8 pouces et nous l’avions multiplié par 8, notre réponse serait en huitièmes d’un pouce. Si nous avions multiplié par 4, notre réponse serait en quatrièmes (ou quarts) d’un pouce.
Étape 3 : Arrondissez la réponse à la fraction la plus proche d’un pouce, puis réduisez la fraction si nécessaire.
Notre réponse finale devient alors :
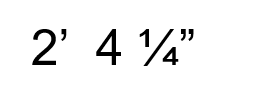
Changez les pieds et les décimales suivants d’un pied en pieds, en pouces et en seizièmes d’un pouce.
Étape 1 : Changez la décimale d’un pied en pouces.
Étape 2 : Il nous reste 8 pouces et les décimales d’un pouce. Le 8 pouces est bon comme il est, mais nous devons changer la décimale d’un pouce en fractions d’un pouce. Nous devons changer la décimale d’un pouce en seizièmes, donc multipliez-la par 16.
Étape 3 : Arrondissez la réponse à la fraction la plus proche d’un pouce, puis réduisez la fraction si nécessaire.
Notre réponse finale devient :
Changez les pieds et les décimales suivants d’un pied en pieds, en pouces et en seizièmes d’un pouce. Mettez votre réponse à l’expression la plus basse et regardez les réponses vidéos lorsque vous avez terminé.
Un élément BCcampus a été exclu de cette version du texte. Vous pouvez le consulter en ligne ici : https://opentextbc.ca/mathfortrades1/?p=184
Un élément BCcampus a été exclu de cette version du texte. Vous pouvez le consulter en ligne ici : https://opentextbc.ca/mathfortrades1/?p=184
15
Nous venons d’apprendre comment changer les fractions en décimales, et maintenant il est temps de faire le contraire. Comment pensez-vous que cela soit fait? Si vous avez deviné que c’est l’inverse de ce que nous venons de faire, alors vous avez raison. Nous commencerons par passer en revue un exemple portant sur le changement des fractions aux décimales, puis nous passerons aux pieds, aux pouces et aux fractions d’un pouce à des pieds et aux décimales d’un pied. Ce que nous cherchons à faire, c’est de :
Encore une fois, la façon rapide et facile de le faire est de passer en revue quelques exemples. Commencez par une fraction et travaillez pour la changer en décimale.
Cela peut se faire de plusieurs façons, la plus simple étant :
Vous pourriez entrer les chiffres dans votre calculatrice, ou vous pourriez utiliser une division non abrégée pour trouver la réponse.
Bon, c’était assez facile, mais passons maintenant à un exemple un peu plus difficile. Nous allons changer un nombre écrit en pieds, pouces et fractions de pouce en une décimale.
Changez ce nombre en décimale :
Étape 1 : Identifiez toute partie du nombre qui est déjà sous une forme qui fonctionne. Dans ce cas, le 7 pieds est bon et il n’est pas nécessaire de le changer.
Étape 2 : Prenez la fraction d’un pouce et transformez-la en décimale.
Prenez une pause ici pour un moment et demandez-vous dans quelle unité se trouve 0.3125 en pouce. Tout ce que nous avons fait est de changer la fraction d’un pouce en décimales d’un pouce. Nous avons maintenant transformé le 9 pouces et les fractions d’un pouce en 9 pouces et les décimales d’un pouce.
Étape 3 : Changer les pouces et les décimales d’un pouce en décimales d’un pied en utilisant le fait que 1 pied = 12 pouces.
Dans la dernière section, quand nous sommes passés des décimales aux fractions, nous avons multiplié par 12 pour obtenir des pouces. Alors que nous faisons le calcul inverse ici en allant des fractions aux décimales, nous finissons par nous diviser par 12 pouces pour obtenir les décimales d’un pied.
Une fois de plus, demandez-vous avec quelles unités vous vous retrouvez ici. Quand on prend les pouces et on les divise par 12, on finit avec des pieds ou, dans ce cas, les décimales d’un pied. Notre réponse finale devient alors :
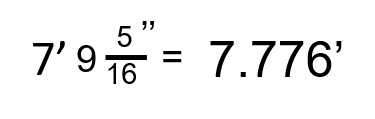
Nous allons passer en revue un autre exemple, et ensuite vous pouvez essayer quelques questions par vous-même après cela.
Modifier le nombre suivant en pieds, en pouces et en fractions de pouce en pieds et en décimales d’un pied.
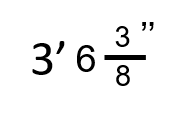
Étape 1 : Identifiez toute partie du nombre qui est déjà sous une forme qui fonctionne. Dans ce cas, le 3 pieds est bon et il n’est pas nécessaire de le changer.
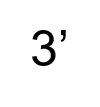
Étape 2 : Prenez la fraction d’un pouce et transformez-la en décimale.
Mettez les pouces et les décimales d’un pouce ensemble.
Étape 3 : Changer les pouces et les décimales d’un pouce en décimales d’un pied en utilisant le fait que 1 pied = 12 pouces.
Notre réponse finale devient alors :
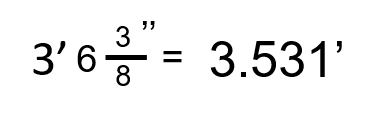
Modifier le nombre suivant en pieds, en pouces et en fractions de pouce en pieds et en décimales d’un pied. Consultez les réponses vidéo pour vous assurer que vous êtes sur la bonne voie.
Un élément BCcampus a été exclu de cette version du texte. Vous pouvez le consulter en ligne ici : https://opentextbc.ca/mathfortrades1/?p=196
Un élément BCcampus a été exclu de cette version du texte. Vous pouvez le consulter en ligne ici : https://opentextbc.ca/mathfortrades1/?p=196
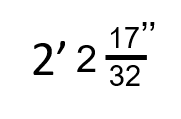
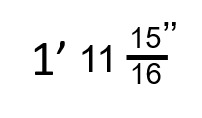
16
11.
Un élément interactif H5P a été exclu de cette version du texte. Vous pouvez le consulter en ligne ici :
https://ecampusontario.pressbooks.pub/mathematiquesdemetier/?p=465#h5p-1
Si vous utilisez la copie papier, PDF ou de livre électronique de ce livre, accédez au lien ci-dessus pour réaliser le jeu-questionnaire. Cependant, les questions du jeu-questionnaire sont également fournies à l’Annexe C à la fin du livre pour une utilisation hors ligne.
IV
Pourcentages
Objectifs
· Définir la notion de pourcentage
· Comprendre les similitudes entre les pourcentages, les rapports et les fractions
· Calculer le pourcentage d’un nombre
· Calculer la variation en pourcentage
17
Vous souvenez-vous de la dernière fois que vous avez écrit un test? Quel pourcentage avez-vous reçu? Si vous avez obtenu 30 sur 35, pourriez-vous calculer le pourcentage? Et si on découvrait le pourcentage d’étudiants qui aiment les mathématiques? Comment calculeriez-vous ce nombre?
Les pourcentages sont utilisés dans de nombreux domaines de notre vie. Par exemple, nous entendons parler du taux d’intérêt ou du taux de chômage, du pourcentage de gens qui préfèrent le hockey au football ou du pourcentage de gens qui préfèrent la science aux mathématiques. Les pourcentages sont un moyen utile de faire des comparaisons. Ce chapitre traitera des pourcentages : comment nous les obtenons, et comment nous pouvons les utiliser.
Le mot « pourcent » signifie « sur 100 ». En mathématiques, quand on dit « sur », cela veut dire « divisé par ». Par conséquent, quand nous parlons de pourcentage, la base est de diviser par 100. Le mot « cent » lorsqu’il est seul fait référence à 100. Le mot cent est en fait le latin pour 100. Cela se rapporte à beaucoup de choses. Le plus facile pourrait être le mot siècle, qui signifie 100 ans.
Vous pouvez aussi penser à des mots comme centimètre. Il y a 100 centimètres (cm) dans 1 mètre. Ou, qu’en est-il du mot cent quand il s’agit d’argent? En ce qui concerne l’argent, 100 cents équivaut à 1 dollar.
Commencez-vous à voir la tendance ici?
Maintenant, pensez à la dernière fois que vous avez répondu à un test sur 100. Disons que vous avez eu une très bonne note et que vous avez obtenu 92 sur 100. Ce serait la même chose que de dire que vous avez reçu 92 pour cent.
Écrit mathématiquement, cela ressemblerait à ceci :
92 %
Le symbole % signifie pourcentage et peut être utilisé au lieu d’écrire le mot pour cent. Vous pouvez trouver ce symbole sur votre clavier d’ordinateur, généralement sur la même touche qu’un des nombres. Sur mon clavier, le symbole de pourcentage est sur la même touche que le chiffre 5. Pour obtenir le symbole %, appuyez simultanément sur les touches[Shift] et[5].
Voici un exemple de pourcentage.
Selon un sondage récent réalisé par les enseignants de BCIT Piping Foundation, 25 % des étudiants inscrits au Piping Foundation Program aimeraient entrer dans le domaine de la plomberie, 20 % aimeraient entrer dans le domaine du montage de tuyaux de vapeur et 10 % aimeraient entrer dans le domaine du montage de tuyaux de gaz. Les 45 % restants des étudiants sont indécis au début du programme. Si vous additionnez ces pourcentages, ils correspondent à 100.
| Métiers de la tuyauterie | Pourcentage |
|---|---|
| Plomberie | 25 % |
| Montage de tuyaux de gaz | 10 % |
| Indécis | 45 % |
| Total | 100 % |
Ce que les chiffres révèlent, c’est que si vous preniez 100 étudiants et leur demandiez quel métier de la tuyauterie ils cherchaient à entrer, en moyenne, 25 diraient plomberie, 20 diraient Mmontage de tuyaux de vapeur, 10 diraient le montage de tuyaux de gaz, et 45 diraient qu’ils sont indécis. (Remarque : Il s’agit de généralisations et non de faits réels.)
Arrêtez-vous ici une seconde! Cela signifie-t-il que chaque fois que vous avez un sondage, et que vous cherchez des pourcentages, vous devez avoir 100 participants?
Non, ce n’est pas le cas.
Nous allons passer en revue cela dans un moment, mais pour l’instant, sachez simplement que les pourcentages sont basés sur 100, mais ne reflètent pas nécessairement que nous avons 100 personnes, éléments, questions, etc.
18
Qu’est-ce qu’un ratio a à voir avec le pourcentage? Qu’est-ce qu’une fraction a à voir avec le pourcentage? Qu’est-ce qu’un ratio? Ce sont toutes de bonnes questions, et nous y répondrons ici. Les pourcentages, les ratios et les fractions sont tous très semblables et peuvent être utilisés pour représenter des nombres de différentes façons, mais avec des résultats semblables.
Nous avons déjà passé en revue les fractions dans un chapitre passé, nous savons donc de quoi il s’agit. Nous devrions prendre un peu de temps pour parler des ratios et de ce qu’ils sont.
Mathématiquement, un ratio est une relation entre deux nombres. Si nous devions encore commander une pizza et manger 3 des 8 tranches, nous pourrions considérer cela comme un ratio. Nous avons mangé trois huitièmes de la pizza. Écrit sous forme de ratio, cela ressemble à :
3 : 8
Notez comment le ratio est écrit. Il a son propre style, tout comme une fraction. Un ratio de 3:8 signifie que nous avons mangé 3 des 8 morceaux de la pizza. Nous pourrions aussi écrire un ratio qui indiquerait combien de morceaux de pizza ont été mangés et combien n’ont pas été mangés. Le ratio pour cela ressemblerait à :
3 : 5
Dans ce cas, 3 morceaux de pizza ont été mangés alors que 5 morceaux n’étaient pas mangés. Quelle que soit la façon dont nous décrivons notre pizza, nous traitons de la relation entre deux nombres.
Voici un autre exemple : disons que nous sommes sur un lieu de travail, et que nous devons installer un tuyau. Nous avons 42 pieds de tuyau en plastique et 79 pieds de tuyau en acier à installer. Quel est le rapport entre les tuyaux en plastique et les tuyaux en acier que nous devons installer?
La réponse :
42 : 79
Une autre question pourrait être de savoir quelle proportion du tuyau est en plastique par rapport à la quantité totale de tuyaux que nous avons. Dans ce cas, le ratio ressemblerait à :
42 : 121
Dans ce cas, le 121 est dérivé de l’addition des longueurs de tuyau en plastique et de tuyau en acier.
42 + 79 = 121
À ce stade, vous pensez peut-être que cela semble familier, et vous auriez raison. Les ratios sont semblables aux fractions, et chaque ratio peut être écrit sous forme de fraction.
Nous dirions que 42 pieds sur un total de 121 pieds de tuyau sont en plastique.
Nous avons ajouté quelques nouvelles choses à notre bibliothèque de mathématiques ici, mais vous vous posez peut-être la question maintenant : « Ne traitons-nous pas des pourcentages dans ce chapitre? Comment tout ce contenu sur les ratios et les fractions se rapportent-ils aux pourcentages? »
L’idée est que nous pouvons prendre ces ratios ou fractions et les transformer en pourcentages en faisant le ratio ou la fraction sur 100. En vérité, nous n’avons même pas besoin de faire un ratio ou une fraction sur 100 pour faire cela, mais c’est un bon endroit pour commencer notre compréhension des mathématiques derrière tout le processus.
Nous sommes à un point où nous pouvons enfin vous présenter de nouvelles personnes dans l’histoire. Pour ce qui est du pourcentage, nous allons utiliser des apprentis du domaine de la menuiserie, de l’électricité et de la plomberie, en plus du domaine des statistiques.
Remarque : toutes les statistiques sont inventées.
Une école de métiers enseigne de nombreux métiers, dont la menuiserie, l’électricité et la plomberie. Il y a actuellement 97 apprentis en menuiserie, 123 apprentis en électricité et 80 apprentis en plomberie à l’école.
L’école aime tenir des statistiques sur les apprentis, y compris le pourcentage de tous les apprentis dans chacun des trois métiers. La question est : comment y parvenir?
La première chose que nous devrions faire est d’additionner le nombre total d’apprentis dans chacun des trois métiers.
Ce que nous pouvons faire maintenant, c’est mettre chaque total d’apprentis dans un ratio et une fraction de l’ensemble.
Si les pourcentages sont basés sur 100, alors nous devons traduire le ratio et la fraction en formes basées sur 100. En d’autres termes, nous devons le faire pour que le nombre à droite dans le ratio soit 100 et que le dénominateur dans la fraction soit 100. Pour cela, nous devons revenir à notre travail avec les fractions.
Nous commencerons par les 97 apprentis en menuiserie. Nous avons 97 apprentis sur un total de 300. Notre objectif ici est de ramener cette fraction à un point où le dénominateur est 100.
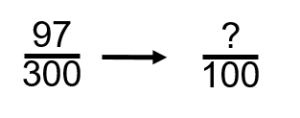
Nous réduisons essentiellement la fraction. Heureusement pour nous, aller de 300 à 100 est assez facile. Nous divisons le dénominateur par 3, puis divisons le numérateur par 3.
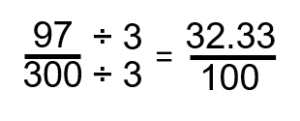
Nous pourrions maintenant écrire ce nombre en tant que ratio.
32.33 : 100
Ce que nous obtenons est le fait que 32,33 % des apprentis des métiers sont des apprentis en menuiserie. Une fois que nous découvrons le nombre d’étudiants en menuiserie par 100 étudiants, nous avons automatiquement notre pourcentage. Dans un instant, nous allons parler de travailler avec des nombres qui ne nous donnent pas un beau nombre comme 100 et qui se traduisent simplement en pourcentage en une seule étape. Mais pour l’instant, continuons avec nos apprentis.
Trouvez le pourcentage d’étudiants en électricité.
Étape 1 : Mettez les nombres dans une équation avec laquelle nous pouvons travailler. Dans ce cas, mettez les nombres dans une fraction.
Étape 2 : Transformez la fraction en une fraction avec un dénominateur de 100.
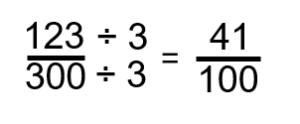
En tant que ratio, nous aurions :
41 : 100
Et enfin, en pourcentage, nous obtenions :
41 %
Calculez maintenant le pourcentage d’apprentis en plomberie. Consultez la vidéo pour voir si votre réponse est la bonne.
Un élément BCcampus a été exclu de cette version du texte. Vous pouvez le consulter en ligne ici : https://opentextbc.ca/mathfortrades1/?p=215
La prochaine étape facilite le processus de recherche des pourcentages. Rappelez-vous que « pourcent » signifie vraiment sur 100, et dans la dernière section, nous avons pris nos nombres et les avons transformés en fractions avec des dénominateurs de 100. Dans cette section, nous ignorons toute la procédure et prenons simplement les nombres que nous avons et travaillons avec eux tels qu’ils sont.
Nous retournerons à nos apprentis pour cela. Sur un total de 97 apprentis en menuiserie, 57 ont la cote « A » ou « B ». Quel pourcentage d’entre eux ont un « A » ou un « B »? Nous pourrions revenir à nos vieilles habitudes et arriver à une fraction avec un dénominateur de 100, ou nous pourrions simplement diviser 57 par 97.
Mathématiquement, cela ressemble à ceci :
Maintenant, prenez le 0,59 et transformez cela en un pourcentage en multipliant le 0,59 par 100. Cela déplace la virgule décimale de 2 à droite et nous laisse avec un nombre entier. C’est aussi simple que cela.
En utilisant la même méthode que celle que nous venons d’utiliser avec les apprentis en menuiserie, trouvez le pourcentage d’étudiants en plomberie à l’école des métiers.
Étape 1 : Notez l’équation dans un format que nous pouvons utiliser.
Étape 2 : Fais cela dans votre tête. C’est une blague : prenez votre calculatrice et entrez les chiffres.
Étape 3 : Multipliez la réponse par 100 pour la mettre en pourcentage.
Essayez ces questions pratiques. Vous pouvez soit changer chaque nombre en une fraction avec un dénominateur de 100, soit diviser un nombre par l’autre. Le choix est à vous, mais les réponses vidéo se feront dans les deux sens.
Les étudiants en électricité câblent un projet électrique dans le cadre de leur note pratique. Les étudiants doivent obtenir au moins 35 points sur 50 possibles. Quel est ce pourcentage?
Un élément BCcampus a été exclu de cette version du texte. Vous pouvez le consulter en ligne ici : https://opentextbc.ca/mathfortrades1/?p=215
On a demandé aux étudiants en plomberie de déplacer un tas de tuyaux d’un côté de l’atelier à l’autre. Il y a 279 morceaux de tuyaux en fonte qui doivent être déplacés. Au bout du compte, ils ont déplacé 222 pièces. Quel pourcentage des tuyaux ont-ils déplacé?
Un élément BCcampus a été exclu de cette version du texte. Vous pouvez le consulter en ligne ici : https://opentextbc.ca/mathfortrades1/?p=215
En ce qui concerne la question 2, quel pourcentage des tuyaux les étudiants doivent-ils encore déplacer par rapport à la quantité initiale?
Un élément BCcampus a été exclu de cette version du texte. Vous pouvez le consulter en ligne ici : https://opentextbc.ca/mathfortrades1/?p=215
19
C’est Noël, et les apprentis ont la chance de gagner le pot de bonbons à la gauche. La seule exigence est qu’ils devinent le nombre de bonbons dans le pot. Bonne réponse = 117
Le gagnant est Bryce, un étudiant en plomberie de niveau 4. Il attribue son succès dans le jeu de comptage des bonbons au fait que sa famille possédait une confiserie quand il était enfant, et que cela a finalement payé.
Bryce décide de donner quelques bonbons. En fait, il décide de donner 12 % à son ami Patrick, 25 % à son ami Matt, et 17 % à son enseignant.
La question qui se pose est de savoir combien représentent chacun de ces pourcentages par rapport au nombre total. Et peut-être qu’à la fin, nous pouvons découvrir combien de bonbons Bryce gardera pour lui-même.
Nous commencerons par Patrick, qui obtiendra 12 % des bonbons. La première chose à faire est de transformer 12 % en une fraction.
Ce que cela nous dira finalement, c’est que pour chaque 100 bonbons qu’il y a dans le pot, Patrick en aura 12. Transformez cette fraction en décimale en divisant 12 par 100.
Avez-vous remarqué une tendance en ce qui concerne les décimales? Voici la relation qui montre quelques différentes façons dont nous pouvons arriver à 12 % :
Ces trois nombres représentent le même montant. Apprendre à travailler entre eux est important en mathématiques, et il est également important de commencer à voir les relations entre les nombres. Revenons à Patrick.
La dernière étape dans cette situation est de prendre le 0,12, qui est actuellement 12 %, et le multiplier par le nombre de bonbons dans le pot.
Maintenant, enlevez 0,04 d’un bonbon est difficile à faire, alors nous allons utiliser nos compétences en arrondissement et arrondirons à 14 bonbons.
Passons maintenant à Matt, le prochain ami de Bryce. Matt obtient 25 % des bonbons.
Étape 1 : Transformez le pourcentage en fraction avec un dénominateur de 100.
Étape 2 : Prenez le 25 et divisez-le par le 100.
Étape 3 : Prenez le 0,25 et multipliez-le par le nombre de bonbons dans le pot.
Nous arrondirons de nouveau vers le bas pour obtenir notre réponse finale de 29.
Nous ne nous inquiéterons pas du nombre de bonbons que l’enseignant reçoit, mais nous calculerons le nombre de bonbons que Bryce garde pour lui-même. Nous voulons calculer le pourcentage de bonbons que Bryce se retrouve avec, et ensuite calculer combien le nombre de bonbons que cela représente.
Étape 1 : Additionnez le pourcentage des bonbons que les trois autres personnes ont, puis soustrayez la somme de 100.
Bryce reçoit 
Étape 2 : À ce stade, nous réalisé quelques exemples dans lesquels nous avons d’abord pris le pourcentage et nous l’avons transformé en une fraction sur 100. Ensuite, nous avons pris le pourcentage et l’avons divisé par 100. Qu’arriverait-il si nous ignorons cette étape? Ce que nous faisons pour un pourcentage, c’est simplement de prendre la virgule et la déplacer de 2 places vers la gauche (cela représente une division par 100). Essayez cela.
Étape 3 : Prenez le 0,46 et multipliez-le par le nombre de bonbons dans le pot.
Cela peut être arrondi à 54. Bryce a encore beaucoup de bonbons, ce qui va satisfaire sa gourmandise, mais il n’en mangera pas jusqu’à ce qu’il devienne malade.
Essayez quelques questions de pratique. Consultez la réponse vidéo pour voir comment vous avez fait.
Un élément BCcampus a été exclu de cette version du texte. Vous pouvez le consulter en ligne ici : https://opentextbc.ca/mathfortrades1/?p=218
Un élément BCcampus a été exclu de cette version du texte. Vous pouvez le consulter en ligne ici : https://opentextbc.ca/mathfortrades1/?p=218
20
Melissa est une étudiante de charpenterie de fondation qui vient de terminer son programme de six mois en fondation. Il s’agit d’un programme destiné aux personnes qui cherchent à se lancer dans le métier, mais qui ne sont pas encore des apprentis.
Il est maintenant temps de gagner de l’argent après avoir passé les six mois précédents à l’école. Après avoir obtenu son diplôme du programme, Melissa a postulé pour trois emplois et a décidé de choisir celui qui offrait la meilleure valeur. Son salaire de départ est de 14 $ par heure, et après six mois, il passera à 16 $ par heure.
Il s’agit d’une augmentation de salaire de 2 $ par heure, mais est-ce que cela représente une bonne augmentation en pourcentage? Si elle commençait à 25 $ par heure et atteignait 27 $ par heure, est-ce que ce serait la même augmentation en pourcentage?
La réponse se trouve dans la formule suivante :
Variation en pourcentage = (Augmentation ou diminution / montant original) x 100
Il y a quelques choses à noter ici. La première est que cette formule fonctionne si vous avez une augmentation ou une diminution par rapport au montant initial. Si le salaire de Melissa diminuait, vous pourriez aussi l’exprimer en pourcentage. La deuxième chose à noter est qu’il y a le nombre 100 à la fin de la formule. Cela est dû au fait que le calcul nous donnerait une décimale, et le fait de multiplier ce nombre par 100 le transforme en un pourcentage.
Donc, pour donner suite à nos calculs, entrons les chiffres et voyons ce que nous obtenons.
Variation en pourcentage = 
Variation en pourcentage = 
Variation en pourcentage = 
Cela nous dit que Melissa obtiendra une augmentation de 14,29 % de son salaire après les six premiers mois. Ce n’est pas mal.
Pendant son programme en fondation, Melissa a dû garder son emploi dans un café pour payer ses factures. Lors de sa première journée de travail, elle a servi 78 tasses de café. Pendant ses six mois au travail, la plus grande quantité de tasses de café qu’elle ait faite en une journée était 201. Comment la différence entre ces montants peut-elle être exprimée en pourcentage d’augmentation?
Étape 1 : Calculer l’augmentation des tasses servies.
Étape 2 : Notez la formule avec laquelle vous allez travailler.
Étape 3 : Entrez les chiffres dans la formule.
Étape 4 : Travaillez pour obtenir la réponse.
Cette réponse nous dit que, du moment où Melissa a commencé à la date où elle a eu sa journée la plus productive, elle a eu une augmentation en un jour de 158 %. Si elle augmentait sa production de 100 %, cela signifierait mathématiquement qu’elle ferait deux fois plus de café qu’avant. Une augmentation de 158 % indique qu’elle fait plus du double de la quantité de café qu’au début.
Répondez aux questions ci-dessous, puis vérifiez les réponses vidéo pour voir votre résultat.
Au cours de sa première année d’exploitation, une école de métiers compte 57 étudiants. Au cours de sa deuxième année d’exploitation, son effectif d’étudiants est passé à 104 étudiants. Quel pourcentage d’augmentation est-ce?
Un élément BCcampus a été exclu de cette version du texte. Vous pouvez le consulter en ligne ici : https://opentextbc.ca/mathfortrades1/?p=224
En ce qui concerne l’école de métiers à la question 1, leur troisième année d’exploitation n’a pas été aussi bonne. Au cours de leur troisième année, le nombre d’étudiants est descendu à 86. Quel pourcentage de diminution est-ce par rapport à la deuxième année?
Un élément BCcampus a été exclu de cette version du texte. Vous pouvez le consulter en ligne ici : https://opentextbc.ca/mathfortrades1/?p=224
L’entreprise pour laquelle Melissa travaille possède actuellement 27 apprentis, et elle veut augmenter ce nombre au cours de l’année à venir. Dans la section précédente, nous aurions demandé combien d’apprentis elle cherche embaucher. Mais si l’objectif était d’augmenter le nombre d’apprentis de 20 %? Comment parviendriez-vous à le faire?
Voici ce que nous avons :
Nous devons intégrer une augmentation de pourcentage pour trouver le nombre d’apprentis que l’entreprise veut avoir au bout du compte. L’entreprise compte actuellement 27 apprentis et elle envisage d’augmenter ce nombre de 20 % au cours de la prochaine année. La première chose que nous devons découvrir est ce que 20 % des 27 est. Rappelez-vous que 20 % est comme 20 sur 100. Nous pouvons utiliser ce concept pour trouver notre réponse.
Multipliez 27 par 0,2 pour obtenir notre augmentation.
Cette réponse indique que l’entreprise veut augmenter son nombre d’apprentis de 5,4. Maintenant, nous ne pouvons pas avoir 0,4 d’apprenti, alors nous devons arrondir vers le haut ou le bas. En suivant les règles que nous avons établies auparavant, nous arrondissons vers le bas pour obtenir 5.
En fin de compte, l’entreprise veut augmenter le nombre d’apprentis de 5. Mais nous n’avons pas encore terminé : nous devons encore calculer le nombre d’apprentis qu’ils veulent avoir à l’avenir. Pour ce faire, nous ajoutons simplement les 5 étudiants supplémentaires à notre nombre de départ, et nous terminons avec 32 étudiants.
Nous allons le changer ici et utiliser les sports à titre d’exemple.
Une équipe professionnelle de hockey a marqué 219 buts au cours de la saison 2018-2019 et a terminé à la 26e place de la ligue. Au cours de la saison 2019-2020, ils veulent améliorer ce total et cherchent une augmentation de 25 % dans la production de buts. Combien de buts devront-ils atteindre pour atteindre leur objectif?
Étape 1 : Calculer 25 % de 219.
Comme nous ne pouvons pas marquer 0,75 d’un but, nous devons arrondir ce résultat à 1 objectif complet et en faire 55 buts supplémentaires.
Étape 2 : Ajoutez 55 à notre nombre d’origine, et nous obtenons :
En fin de compte, pour atteindre l’augmentation de 25 % de la production de buts qu’ils recherchent, l’équipe devrait marquer 274 buts. S’ils avaient marqué autant de buts au cours de la saison 2018-2019, ils se retrouveraient dans les 5 ou 6 meilleures équipes pour la production de buts.
;
Répondez aux questions suivantes et vérifiez les réponses vidéo pour voir votre résultat.
Melissa, l’apprentie en menuiserie, aime jardiner au printemps et en été. Cette année, elle a planté 42 plantes. L’année prochaine, elle veut augmenter le nombre total de plantes de 15 %. Combien de plantes devra-t-elle planter pour atteindre son objectif?
Un élément BCcampus a été exclu de cette version du texte. Vous pouvez le consulter en ligne ici : https://opentextbc.ca/mathfortrades1/?p=224
Revenons au sport pour celle-ci. Un quarter-arrière a lancé 47 passes de touché en un an. L’année suivante, le nombre de passes de touché qu’il a lancé a chuté de 35 %. Combien de passes de touché a-t-il effectuées cette année-là?
Un élément BCcampus a été exclu de cette version du texte. Vous pouvez le consulter en ligne ici : https://opentextbc.ca/mathfortrades1/?p=224
21
21.
Un élément interactif H5P a été exclu de cette version du texte. Vous pouvez le consulter en ligne ici :
https://ecampusontario.pressbooks.pub/mathematiquesdemetier/?p=493#h5p-4
Si vous utilisez la version imprimée, PDF ou électronique du présent livre, rendez-vous sur le lien ci-dessus pour répondre au questionnaire. Cependant, les questions du jeu-questionnaire sont également fournies dans l’Annexe C à la fin du livre pour une utilisation hors ligne.
1
2
| 1 × 1 = | 1 |
| 1 × 2 = | 2 |
| 1 × 3 = | 3 |
| 1 × 4 = | 4 |
| 1 × 5 = | 5 |
| 1 × 6 = | 6 |
| 1 × 7 = | 7 |
| 1 × 8 = | 8 |
| 1 × 9 = | 9 |
| 1 × 10 = | 10 |
| 1 × 11 = | 11 |
| 1 × 12 = | 12 |
| 2 × 1 = | 2 |
| 2 × 2 = | 4 |
| 2 × 3 = | 6 |
| 2 × 4 = | 8 |
| 2 × 5 = | 10 |
| 2 × 6 = | 12 |
| 2 × 7 = | 14 |
| 2 × 8 = | 16 |
| 2 × 9 = | 18 |
| 2 × 10 = | 20 |
| 2 × 11 = | 22 |
| 2 × 12 = | 24 |
| 3 × 1 = | 3 |
| 3 × 2 = | 6 |
| 3 × 3 = | 9 |
| 3 × 4 = | 12 |
| 3 × 5 = | 15 |
| 3 × 6 = | 18 |
| 3 × 7 = | 21 |
| 3 × 8 = | 24 |
| 3 × 9 = | 27 |
| 3 × 10 = | 30 |
| 3 × 11 = | 33 |
| 3 × 12 = | 36 |
| 4 × 1 = | 4 |
| 4 × 2 = | 8 |
| 4 × 3 = | 12 |
| 4 × 4 = | 16 |
| 4 × 5 = | 20 |
| 4 × 6 = | 24 |
| 4 × 7 = | 28 |
| 4 × 8 = | 32 |
| 4 × 9 = | 36 |
| 4 × 10 = | 40 |
| 4 × 11 = | 44 |
| 4 × 12 = | 48 |
| 5 × 1 = | 5 |
| 5 × 2 = | 10 |
| 5 × 3 = | 15 |
| 5 × 4 = | 20 |
| 5 × 5 = | 25 |
| 5 × 6 = | 30 |
| 5 × 7 = | 35 |
| 5 × 8 = | 40 |
| 5 × 9 = | 45 |
| 5 × 10 = | 50 |
| 5 × 11 = | 55 |
| 5 × 12 = | 60 |
| 6 × 1 = | 6 |
| 6 × 2 = | 12 |
| 6 × 3 = | 18 |
| 6 × 4 = | 24 |
| 6 × 5 = | 50 |
| 6 × 6 = | 36 |
| 6 × 7 = | 42 |
| 6 × 8 = | 48 |
| 6 × 9 = | 54 |
| 6 × 10 = | 60 |
| 6 × 11 = | 66 |
| 6 × 12 = | 72 |
| 7 × 1 = | 7 |
| 7 × 2 = | 14 |
| 7 × 3 = | 21 |
| 7 × 4 = | 28 |
| 7 × 5 = | 35 |
| 7 × 6 = | 42 |
| 7 × 7 = | 49 |
| 7 × 8 = | 56 |
| 7 × 9 = | 63 |
| 7 × 10 = | 70 |
| 7 × 11 = | 77 |
| 7 × 12 = |
| 8 × 1 = | 8 |
| 8 × 2 = | 16 |
| 8 × 3 = | 24 |
| 8 × 4 = | 32 |
| 8 × 5 = | 40 |
| 8 × 6 = | 48 |
| 8 × 7 = | 56 |
| 8 × 8 = | 64 |
| 8 × 9 = | 72 |
| 8 × 10 = | 80 |
| 8 × 11 = | 88 |
| 8 × 12 = | 96 |
| 9 × 1 = | 9 |
| 9 × 2 = | 18 |
| 9 × 3 = | 27 |
| 9 × 4 = | 36 |
| 9 × 5 = | 45 |
| 9 × 6 = | 54 |
| 9 × 7 = | 63 |
| 9 × 8 = | 72 |
| 9 × 9 = | 81 |
| 9 × 10 = | 90 |
| 9 × 11 = | 99 |
| 9 × 12 = | 108 |
| 10 × 1 = | 10 |
| 10 × 2 = | 20 |
| 10 × 3 = | 30 |
| 10 × 4 = | 40 |
| 10 × 5 = | 50 |
| 10 × 6 = | 60 |
| 10 × 7 = | 70 |
| 10 × 8 = | 80 |
| 10 × 9 = | 90 |
| 10 × 10 = | 100 |
| 10 × 11 = | 110 |
| 10 × 12 = | 120 |
| 11 × 1 = | 11 |
| 11 × 2 = | 22 |
| 11 × 3 = | 33 |
| 11 × 4 = | 44 |
| 11 × 5 = | 55 |
| 11 × 6 = | 66 |
| 11 × 7 = | 77 |
| 11 × 8 = | 88 |
| 11 × 9 = | 99 |
| 11 × 10 = | 110 |
| 11 × 11 = | 121 |
| 11 × 12 = | 132 |
| 12 × 1 = | 12 |
| 12 × 2 = | 24 |
| 12 × 3 = | 36 |
| 12 × 4 = | 48 |
| 12 × 5 = | 60 |
| 12 × 6 = | 72 |
| 12 × 7 = | 84 |
| 12 × 8 = | 96 |
| 12 × 9 = | 108 |
| 12 × 10 = | 120 |
| 12 × 11 = | 132 |
| 12 × 12 = | 144 |
| × | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 |
| 1 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| 2 | 0 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 | 18 | 20 | 22 | 24 |
| 3 | 0 | 3 | 6 | 9 | 12 | 15 | 18 | 21 | 24 | 27 | 30 | 33 | 36 |
| 4 | 0 | 4 | 8 | 12 | 16 | 20 | 24 | 28 | 32 | 36 | 40 | 44 | 48 |
| 5 | 0 | 5 | 10 | 15 | 20 | 25 | 30 | 35 | 40 | 45 | 50 | 55 | 60 |
| 6 | 0 | 6 | 12 | 18 | 24 | 30 | 36 | 42 | 48 | 54 | 60 | 66 | 72 |
| 7 | 0 | 7 | 14 | 21 | 28 | 35 | 42 | 49 | 56 | 63 | 70 | 77 | 84 |
| 8 | 0 | 8 | 16 | 24 | 32 | 40 | 48 | 56 | 64 | 72 | 80 | 88 | 96 |
| 9 | 0 | 9 | 18 | 27 | 36 | 45 | 54 | 63 | 72 | 81 | 90 | 99 | 108 |
| 10 | 0 | 10 | 20 | 30 | 40 | 50 | 60 | 70 | 80 | 90 | 100 | 110 | 120 |
| 11 | 0 | 11 | 22 | 33 | 44 | 55 | 66 | 77 | 88 | 99 | 110 | 121 | 132 |
| 12 | 0 | 12 | 24 | 36 | 48 | 60 | 72 | 84 | 96 | 108 | 120 | 132 | 144 |
3
3 = cent millions
8 = dix millions
5 = millions
9 = cent milliers
2 = dix milliers
2 = milliers
1 = centaines
0 = dizaines
2 = unités
2 = dix milliards
0 = milliards
4 = cent millions
3 = dix millions
3 = millions
8 = cent milliers
7 = dix milliers
6 = milliers
0 = centaines
1 = dizaines
1 = unités
4
Trouver la valeur manquante.
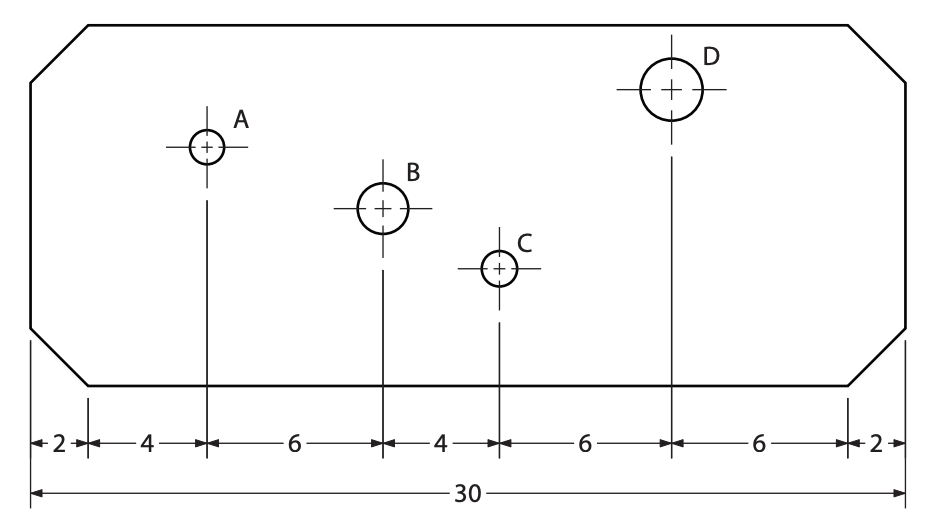Au total, 256 pièces moulées en bronze ont été usinées. Chaque pièce coulée avait une masse de 793 g, et 158 g ont été retirés de chacune par usinage. La masse totale de bronze retiré par usinage était de 162 560 g. Vrai ou faux?Pour répondre au questionnaire à l’ordinateur, cliquez sur le lien à la page précédente. Lorsque vous remplirez le questionnaire à l’ordinateur, les questions seront aléatoires. Les mêmes questions sont fournies ci-dessous.
5
Les fichiers publiés par cet ouvrage reflètent toujours la version la plus récente. Si vous trouvez une erreur dans ce manuel, veuillez remplir le formulaire « Signaler une erreur dans le manuel ouvert ».
| Version | Date | Changements | Détails |
|---|---|---|---|
| 1,00 | 17 avril 2020 | Ajout à la collection B.C. Open Textbook. | |
| 1.01 | 24 juillet 2020 | Correction du questionnaire sur les nombres entiers et du questionnaire sur les fractions. | Nombres entiers : Ajout de « 86 » à la liste des nombres dans la question sur les boîtes de commutation. Fractions : La fraction de la question sur l’acier a été modifiée de 11/2 à 1½. |