Mathématiques pour les professions de la santé publique et au travail Copyright © 2024 by eCampusOntario is licensed under a License Creative Commons Attribution - Partage dans les mêmes conditions 4.0 International, except where otherwise noted.
Mathématiques pour les professions de la santé publique et au travail Copyright © 2024 by eCampusOntario is licensed under a License Creative Commons Attribution - Partage dans les mêmes conditions 4.0 International, except where otherwise noted.
1

Mathématiques pour les professions de la santé publique et au travail de Ian Young est autorisé en vertu d’une licence internationale Attribution – Partage dans les mêmes conditions 4.0 de Creative Commons, sauf indication contraire.
Veuillez consulter la section Remerciements du manuel pour les sources des ressources éducatives libres (REL) utilisées dans la création de ce dernier.
Ce manuel a été réalisé en collaboration avec Pressbooks.
2
Chapitre 1 : Révision d’algèbre
1.4. Rapports, taux et pourcentage
1.5. Exposants et notation scientifique
1.6. Réponses à l’exercice pratique
Chapitre 2 : Équations linéaires et représentations graphiques
2.1. Représentation graphique d’une équation linéaire
2.5. Réponses à l’exercice pratique
Chapitre 3 : Introduction aux fonctions
3.1. Introduction aux fonctions
3.3. Dérivée et comportement des représentations graphiques
3.5. Réponses à l’exercice pratique
Chapitre 4 : Fonctions exponentielles et logarithmiques
4.3. Modèles exponentiels et logarithmiques
4.4. Réponses à l’exercice pratique
Chapitre 5 : Ensembles et dénombrement
5.1. Théorie des ensembles et diagrammes de Venn
5.5. Réponses à l’exercice pratique
Chapitre 6 : Probabilité – Partie 1
6.1. Espaces échantillons et probabilité
6.2. Événements mutuellement exclusifs et règle de l’addition
6.3. Probabilité à l’aide de schémas en arbre et de combinaisons
6.4. Probabilité conditionnelle
6.6. Réponses à l’exercice pratique
Chapitre 7 : Probabilité – Partie 2
3
La matière est destinée à des étudiant.e.s en santé publique et au travail de la première année du premier cycle aux différents bagages de connaissances en mathématiques. La matière vise à préparer les étudiant.e.s pour des cours quantitatifs plus avancés en biostatistique, en épidémiologie et en évaluation des risques, notamment.
4
Wang, M. (2018) Key Concepts of Intermediate Level Math. Victoria, C.-B. : BCcampus.
Contenu adapté des unités 2, 4 à 7, 9 et 11.
Ce texte est autorisé en vertu d’une licence Attribution de Creative Commons.
Sekhon, R. (2011). Applied Finite Mathematics. Houston, TX : OpenStax
Contenu adapté des chapitres 1, 11, 13, 15 et 17 (section 1-3).
Ce texte est autorisé en vertu d’une licence Attribution de Creative Commons.
Lippman, D. (2016). Business Precalculus.
Contenu adapté des chapitres 1 (p. 1 à 22, 24 à 26), 4 (p. 153 à 163) et 5.
Ce texte est autorisé en vertu d’une licence Attribution – Partage dans les mêmes conditions 3.0 États-Unis de Creative Commons.
Le contenu a été adapté pour Pressbooks par Angelica Chimal, adjointe aux publications numériques de CareerBoost et étudiante au B. Sc. à l’Université Ryerson, avec le soutien de l’équipe de publication numérique de la bibliothèque de l’Université Ryerson.
L’image de la couverture a été prise par Samuel Zeller sur Unsplash
I
1
Révision des termes algébriques de base :
| Terme algébrique | Description | Exemple |
| Expression algébrique | Phrase mathématique contenant des nombres, des variables (lettres) et des opérations arithmétiques (+, – , ×, ÷, etc.). | Terme | Un terme peut être une constante, une variable ou le produit d’un nombre et d’une variable. (Les termes sont séparés par un signe plus ou un signe moins). | Polynôme : expression algébrique contenant un ou plusieurs termes. Exemples : 7x , 5ax – 9b , 6x2 – 5x +
Il existe des noms spéciaux pour les polynômes qui possèdent un, deux ou trois termes :
Exemples : 9x , 4xy2 , 0,8mn2 ,
Exemples : ax2+ bx + c , – 4qp2 + 3q + 5
Combinaison de termesTermes semblables : termes qui ont les mêmes variables et exposants (qui ne diffèrent que par leurs coefficients). Exemples :
Combinaison de termes semblables : ajouter ou soustraire leurs coefficients et conserver les mêmes variables et exposants. Remarque : Les termes non semblables ne peuvent pas être combinés.
Suppression des parenthèsesSi le signe précédant les parenthèses est positif (+), ne changez pas le signe des termes à l’intérieur des parenthèses, supprimez simplement les parenthèses. Exemple : (x– 5) = x– 5 Si le signe précédant les parenthèses est négatif (-), supprimez les parenthèses et le signe négatif (devant les parenthèses), et changez le signe de chaque terme à l’intérieur des parenthèses. Exemple : – (x– 7) = –x + 7
Supprimer les parenthèses :
Multiplication et division d’expressions algébriquesMultiplication d’un monôme et d’un polynôme :
Division d’un polynôme par un monôme :
La méthode FOIL (développement) : une manière simple de trouver le produit de deux binômes (deux termes).
Multiplication de binômes (2 termes × 2 termes) : F O I L | La méthode FOIL (développement). | |||||||||||||||||||||||||||||||||||||||||||||||||||
| an am = an+ m | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Combiner les termes semblables. |
| 2) | Méthode FOIL (développement) |
| an am = an+m | |
| Combiner les termes semblables. |
| 3) | Méthode FOIL (développement) |
| an am = an+m | |
| Combiner les termes semblables. |
| 4) | Méthode FOIL (développement) |
| Combiner les termes semblables. |
1. Identifier les termes de chaque polynôme :
2. Combiner les termes semblables :
3. Simplifier :
2
Équation : phrase mathématique contenant deux expressions et séparée par un signe d’égalité (les deux côtés de l’équation ont la même valeur).
Pour résoudre une équation, nous trouvons une valeur particulière pour la variable de l’équation qui rend l’équation vraie (côté gauche = côté droit).
Exemple : Pour l’équation x + 4 = 5
seul x = 1 peut être vrai, puisque 1 + 4 = 5 (côté gauche = côté droit).
Solution d’une équation : valeur de la variable dans l’équation qui rend l’équation vraie.
Indiquez si chacun des nombres donnés est une solution à l’équation donnée.
| 1) 2 : 4x – 3 = 5 | 4 ∙ 2 – 3 | 5 | Oui | Remplacer x par 2. |
| 2) 15 : | -3 | Oui | Remplacer y par 15. |
| 3) | 8 ( | 4 ≠ 3 | Non | Impossible de remplacer t par |
Propriétés pour la résolution d’équations :
| Propriétés | Égalité | Exemples |
| Propriété d’addition d’une égalité | A = B A + C = B + C | Résoudre
|
| Propriété de soustraction d’une égalité | A = B A – C = B – C | Résoudre
|
| Propriété de multiplication d’une égalité | A = B A · C = B · C | Résoudre
|
| Propriété de division d’une égalité | A = B | Résoudre
|
Résoudre les équations suivantes.
| 1) | Propriété d’addition. | |
| Vérifier : | Remplacer x par 14. |
| 2) | Propriété de soustraction. | |
| 3) | Propriété de multiplication. | |
| 4) | Propriété de division. | |
Procédure pour résoudre les équations à plusieurs étapes :
Effacer les fractions ou les décimales si nécessaire. Simplifier et supprimer les parenthèses si nécessaire. Combiner les termes semblables de chaque côté de l’équation. Rassembler les termes variables d’un côté de l’équation et les constantes de l’autre côté. Isoler la variable (pour obtenir la variable seule d’un côté de l’équation). Vérifier la solution à l’aide de l’équation originale.
Étapes Exemples
Résoudre Éliminer les dénominateurs si l’équation comporte des fractions.
Multiplier chaque terme par 5. Supprimer les parenthèses.
Combiner les termes semblables.
Rassembler les termes variables d’un côté et les constantes de l’autre.
Soustraire 10 des deux côtés. Soustraire 6y des deux côtés. Isoler la variable.
Diviser les deux côtés par 5. Vérifier la solution à l’aide de l’équation originale.
Remplacer y par 2. Multiplier chaque terme par 5. Côté gauche = côté droit (bonne réponse)
Équations avec décimales : multiplier chaque terme des deux côtés de l’équation par un multiple de 10 (10, 100, 1 000, etc.) pour supprimer les décimales (en vous basant sur le nombre ayant le plus grand nombre de décimales dans l’équation).
Étapes Exemples
Résoudre Multiplier chaque terme par 100 pour supprimer les décimales.
Le plus grand nombre de décimales est deux. Rassembler les termes variables d’un côté de l’équation et les constantes de l’autre côté.
Ajouter 12 de chaque côté. Ajouter 426x de chaque côté. Isoler la variable.
Exemple 1.2.3
| Résoudre 0,4y + 0,08 = 0,016 | Le plus grand nombre de décimales est trois. |
| 1000(0,4y) + 1000(0,08) = 1000(0,016) | Multiplier chaque terme par 1 000. |
| 400y + 80 = 16 | Combiner les termes semblables. |
| 400y = -64 | Diviser les deux côtés par 400. |
| y = – 0,16 |
Équations avec fractions :
| Étapes | Exemples |
| Résoudre | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Problèmes verbauxIdentification des mots-clés :
Mots-clés ou indices dans les problèmes verbaux :
1) Edward a conduit de Prince George à Williams Lake (235 km), puis à Cache Creek (203 km) et enfin à Vancouver (390 km). Combien de kilomètres Edward a-t-il parcourus au total?
2) Vendredi, Emma avait 150 dollars dans son portefeuille. Elle a acheté une pizza pour 15 dollars et une paire de chaussures pour 35 dollars. Combien d’argent lui reste-t-elle?
3) Lucy a reçu de Marc un loyer mensuel de 950 $ pour les mois de septembre à novembre. Combien a-t-elle perçu au total?
4) Julia va acheter à son oncle une voiture d’occasion d’une valeur de 7 500 $. Elle promet de payer 500 $ par mois. En combien de mois pourra-t-elle rembourser sa voiture?
Étapes de la résolution des problèmes verbaux :
William a acheté 5 paires de chaussettes pour 4,35 $ chacune. Le caissier lui a facturé un supplément de 2,15 $ pour la taxe de vente. Il a quitté le magasin avec un maigre 5,15 $. Combien d’argent William avait-il au départ?
Exemples supplémentaires : James avait 96 jouets. Il en a vendu 13 le premier jour, 32 le deuxième jour, 21 le troisième jour, 14 le quatrième jour et 7 le dernier jour. Quel est le pourcentage de jouets non vendus?
Le réservoir d’essence de 60 litres de la voiture de Robert est à moitié plein. Kelowna est à environ 390 km de Vancouver et sa voiture consomme en moyenne 7 litres aux 100 km. Robert peut-il se rendre à Vancouver?
Exercices pratiques1. Résoudre les équations suivantes : 2. Écrire une expression pour chacun des éléments suivants :
|
3
Systèmes de mesure
Système métrique (SI – système international d’unités) : Le système de mesure le plus utilisé dans le monde. Il repose sur les unités de base que sont le mètre, le kilogramme, la seconde, etc.
Unités communes du système international :
| Quantité | Unité | Symbole de l’unité |
| Longueur | mètre | m |
| Masse (ou poids) | gramme | g |
| Volume | litre | L |
| Durée | seconde | s |
| Température | degré (Celsius) | °C |
Préfixes métriques (préfixes du système international) : Les préfixes du système international sont fondés sur les multiples de 10.
Tableau de conversion métrique :
| Préfixe | Symbole (abréviation) | Puissance de 10 | Valeur | Exemples |
| méga- | M | 106 | 1 000 000 | 1 Mm = 1 000 000 m |
| kilo- | k | 103 | 1 000 | 1 km = 1 000 m |
| hecto- | h | 102 | 100 | 1 hm = 100 m |
| déca- | da | 101 | 10 | 1 dam = 10 m |
| mètre/gramme/litre | 1 | |||
| déci- | d | 10-1 | 0,1 | 1 m = 10 dm |
| centi- | c | 10-2 | 0,01 | 1 m = 100 cm |
| milli- | m | 10-3 | 0,001 | 1 m = 1 000 mm |
| micro | µ | 10-6 | 0,000 001 | 1 m = 1 000 000 µm |
Préfixes métriques pour la longueur, le poids et le volume :
| Préfixe | Longueur (m – mètre) | Poids (g – gramme) | Volume de liquide (L – litre) |
| méga (M) | Mm (mégamètre) | Mg (mégagramme) | ML (mégalitre) |
| kilo (k) | km (kilomètre) | kg (kilogramme) | kL (kilolitre) |
| hecto (h) | hm (hectomètre) | hg (hectogramme) | hL (hectolitre) |
| déca (da) | dam (décamètre) | dag (décagramme) | daL (décalitre) |
| mètre/gramme/litre | m (mètre) | g (gramme) | L (litre) |
| déci (d) | dm (décimètre) | dg (décigramme) | dL (décilitre) |
| centi (c) | cm (centimètre) | cg (centigramme) | cL (centilitre) |
| milli (m) | mm (millimètre) | mg (milligramme) | mL (millilitre) |
| micro (µ) | µm (micromètre) | µg (microgramme) | µL (microlitre) |
Étapes de la conversion métrique :
326 mm = (?) m
4,675 hg = (?) g
Cette méthode permet de convertir une unité dans une autre.
1 200 g = (?) kg
30 cm = (?) mm
Addition et soustraction de mesures du système international :
Combiner après conversion dans la même unité.
| 3 m | 3 000 mm | 1 m = 1 000 mm | |
| – 2 000 mm | ——–> | – 2 000 mm | |
| 1 000 mm |
| 25 kg | 25 000 g | 1 kg = 1 000 g | |
| + 4 g | ——–> | + 4 g | |
| 25 004 g |
Quel est le rapport entre mL, g et cm3?
Convertir les unités suivantes.
| 1) 16 cm3 = ( ? ) g | |
| 16 cm3 = 16 g | 1 cm3 = 1 g |
| 2) 9 L = ( ? ) cm3 | |
| 9 L = 9 000 mL | 1 L = 1 000 mL |
| = 9 000 cm3 | 1 mL = 1 cm3 |
| 3) 35 cm3 = (?) cL | |
| 35 cm3 = 35 mL | 1 cm3 = 1 mL |
| = 3,5 cL | La virgule fait un bond vers la gauche. |
| 4) 450 kg = (?) L | |
| 450 kg = 450 000 g | 1 kg = 1 000 g |
| = 450 000 mL | 1 g = 1 mL |
| = 450 L | 1 L = 1 000 mL |
Une piscine mesure 10 m x 8 m x 2 m. Combien de kilolitres d’eau peut-elle contenir?
| V = largeur x longueur x hauteur = (8 m) (10 m) (2 m) = 160 m3 | 160 m3 = ( ? ) kL |
| 160m3 = 160 000 000 cm3 | 1 m = 100 cm, 3 × 2 = 6, déplacez la virgule de six positions vers la droite pour connaître le volume. |
| 160 000 000 cm3 = 160 000 000 mL | 1 mL = 1 cm3 |
| 160 000 000 mL = 160 kL | 1 kL = 1 000 000 mL |
| 160 m3 = 160 kL | La piscine peut contenir 160 kL d’eau. |
1.Convertissez les mesures suivantes.
3. Combinez les unités suivantes.
4. Complétez les équations suivantes.
4
Rapport : relation entre deux nombres, exprimée sous forme de quotient avec la même unité au dénominateur et au numérateur. Il existe trois façons d’écrire un rapport.
Exemple : Écrire le rapport entre 5 cents et 9 cents.
Taux : rapport entre deux quantités d’unités différentes.
Exemple : enseignants à étudiants; argent à temps; distance à temps, etc.
Exemple : 80 kilomètres pour 320 minutes :
Taux unitaire : taux dans lequel le nombre au dénominateur est 1.
Proportion : équation dont les deux côtés présentent un rapport (ou un taux) ().
Exemple : Transformons la phrase suivante en proportion.
3 imprimantes correspondent à 18 ordinateurs, tandis que 2 imprimantes correspondent à 12 ordinateurs.
Résolution d’une proportion :
4 litres de lait coûtent 4,38 $, combien coûtent 2 litres ?
|
| 4 L de lait | 2 L de lait |
| 4,38 $ | x $ = ? |
| ||
| ||
| Diviser les deux côtés par 4. | |
| 2 litres de lait coûtent 2,19 dollars. | ||
| Remplacer x par 2,19. | |
| (4) (2,19) = (2) (4,38) | ||
| 8,76 = 8,76 | Bonne réponse! |
Tom mesure 1,75 mètre et son ombre mesure 1,09 mètre. L’ombre d’un bâtiment mesure 10 mètres de long au même moment. Quelle est la hauteur du bâtiment?
|
| Taille de Tom = 1,75 m | Hauteur du bâtiment (x) = ? |
| Ombre de Tom = 1,09 m | Ombre du bâtiment = 10 m |
| ||
| ||
| Diviser les deux côtés par 1,09. | |
| La hauteur du bâtiment est de 16,055 m. | ||
| Remplacer x par 16,055. | |
| Bonne réponse! |
Si 15 mL de médicament doivent être mélangés à 180 mL d’eau, combien de millilitres de médicament doivent être mélangés à 230 mL d’eau?
| ||
| ||
| ||
| 19,17 mL de médicament doivent être mélangés à 230 mL d’eau. | ||
Pourcentage (%) : une partie pour cent.
Conversion entre pourcentages, décimales et fractions :
| Conversion | Étapes | Exemples |
| Pourcentage ⇒ Décimale | Déplacer la virgule de deux positions vers la gauche, puis supprimer le symbole %. | 31 % = 31, % = 0,31 |
| Décimale ⇒ Pourcentage | Déplacer la virgule de deux positions vers la droite, puis ajouter le symbole %. | 0,317 = 0, 317 = 31,7 % |
| Pourcentage ⇒ Fraction | Enlever le %, diviser par 100, puis simplifier. | 15 % = |
| Fraction ⇒ Pourcentage | Diviser, déplacer la virgule de deux positions vers la droite, puis ajouter le symbole %. | |
| Décimale ⇒ Fraction | Convertir la décimale en pourcentage, puis convertir le pourcentage en fraction. | 0,35 = 35 % = % = pour cent |
Il existe deux méthodes pour résoudre les problèmes de pourcentage :
Méthode des proportions en pourcentage :
| ou |
| Étapes | Exemples |
| 8 pour cent de quel nombre est 4? | ||||
| ⇑ Pourcentage | ⇑ Tout (x) | ⇑ Partie | |
| ||||
| ||||
Méthode de traduction : traduire les mots en symboles mathématiques.
1) Quel est 15 % de 80?
x = 0,15 • 80 x = (0,15)(80) = 12
2) Quel pourcentage de 90 est 45?
x % • 90 = 45 x % = = 0,5 = 50 %
3) 12 est 8 % de quel nombre?
12 = 0,08 • x x = = 150
Pourcentage d’augmentation ou de diminution :
| Application | Formule |
| Pourcentage d’augmentation | Pourcentage d’augmentation = | |
| Pourcentage de réduction | Pourcentage de diminution = |
La production d’un bien est passée de 1 500 unités le mois dernier à 1 650 ce mois-ci. Trouvez le pourcentage d’augmentation.
| Nouvelle valeur (N) | 1 650 | Ce mois-ci. |
| Valeur originale (O) : | 1 500 | Le mois dernier. |
| Pourcentage d’augmentation : | Une augmentation de 10 %. |
La production a été réduite de 33 à
29. Quel est le pourcentage de réduction?
| Pourcentage de réduction : | Une réduction de 12 %. |
1. Exprimez les données suivantes sous forme de rapport ou de taux simplifié.
2. Un train a parcouru 459 km en 6 heures. Quel est le taux unitaire?
3. Exprimez la phrase suivante à l’aide d’une proportion : 24 heures correspondent à 1 940 kilomètres et 12 heures à 985 kilomètres.
4. 4 litres de jus de fruit coûtent 7,38 $. Combien coûtent 2 litres?
5. Sarah gagne 4 500 $ en 30 jours. Combien gagne-t-elle en 120 jours?
6. Un produit a vu sa production passer de 2 800 unités l’année dernière à 3 920 unités cette année. Trouvez le pourcentage d’augmentation.
7. Le tableau ci-dessous présente des données sur le chômage des étudiants en santé publique de l’Université métropolitaine de Toronto durant l’été, mais certaines données sont manquantes :
| Année | 2015 | 2016 | 2017 |
| Étudiants au chômage | 350 | ? | 396 |
| Nombre total d’étudiants | 1 250 | 1 100 | ? |
5
Retour sur les exposants : an ou baseexposant
| Notation exponentielle | Exemples |
| Base Exposant | |
| an= a ∙ a ∙ a ∙ a … a | 24 = 2 ∙ 2 ∙ 2 ∙ 2 = 16 |
| Lire « a exposant n » ou « a à la n ». | Lire « 2 exposant 4 ». |
Propriétés des exposants :
| Noms | Règles | Exemples |
| Règle du produit | ||
| Règle du quotient | ||
| Règle de la puissance | ||
| Exposant négatif a-n | ||
| Exposant zéro a0 | ||
| Exposant un a1 | ||
| Exposant fractionnaire |
Cette règle peut également démontrer pourquoi a0 = 1 (exposant zéro a0) :
Simplifiez (ne laissez pas d’exposants négatifs dans la réponse).
| 1) | |
| 2) | |
| 3) | |
| 4) | |
| 5) | |
| 6) | |
| 7) | |
| 8) | |
| 9) | |
| 10) |
Simplifier.
| 1) | ||
| Supprimer les parenthèses. | ||
| Regrouper les coefficients et les variables. | ||
| Simplifier. | ||
| Rendre l’exposant positif. |
| 2) | ||
| Supprimer les parenthèses. | ||
| Regrouper les coefficients et les variables. | ||
| Simplifier. |
Soit a = 2, b = 1, c = -1.
| 1) |
| 2) | Remplacer a par 2 et b par 1. |
| 3) | Remplacer a par 2, b par 1 et c par -1. |
Notation scientifique
La notation scientifique est un moyen particulier d’exprimer de manière concise les très grands et les très petits nombres.
Exemple : 300 000 000 = 3 × 108 m/sec La vitesse de la lumière.
Notation scientifique : produit d’un nombre compris entre 1 et 10 et d’une puissance de 10.
| Notation scientifique | Exemple |
| N × 10±n | 1 ≤ N < 10 | 67504,3 = 6,75043 × 104 | |
| n – nombre entier | Forme standard | Notation scientifique | |
Écrire un nombre en notation scientifique :
| Étapes | Exemples |
| Écrire en notation scientifique. 1) 2340000 = 2340000, = 2,34 × 106 6 positions vers la gauche, × 10n 2) 0,000000439 = 4,39 × 10-7 7 positions vers la droite, × 10-n
Écrivons les nombres suivants en forme standard. 1) 6,4275 ×104 = 64275 2) 2,9 × 10-3 = 0,0029
Exercices pratiques1. Calculez : 2. Simplifiez (ne laissez aucun exposant négatif dans la réponse) : 3. Écrivez en notation scientifique : 4. Écrivez en forme standard :
|
6
1.a. 5x3 , 8x2 , 2x
b. –y4 , 9a2 , a , –1
2.a. –x + 19y
b. 6a2 – 31b
c. 9 m 2 + 64 n
3.a. 10a2 + 13
b. -19x + 39y
c. 17ab – 28xy
d. 40y2– 11y– 63
e. 21r2 + 28rt2– 6rt –8t3
f. x2–x +
1.a. x = 19
b. y =
c. x =
d. t =
e. x = 2
f. y =
g. t = – 0,05
h. x =
2. a. 375 $ + y
b. 175 – y
c. 45 – w
d. ,
1.a. 0,439 m
b. 0,0000483 kL
c. 7,23 kg
d. 520 mm
3. a. 4 000 mm
b. 63 006 g
4. a. 38 g
b. 5 000 cm3
c. 18 000 cm3
d. 0,039375 kL
1.a.
b.
c.
2. 76,5 km/h
3.
4. 3,69 $
5. 18 000 $
6. 40 %
7.a. 28 %
b. 308
c. 1 200
1. a. 24
b. 982
2. a. – 92
b. y 7
c. x 3
d.
e. 81a8b12
f.
g.
3. a. 4,56 × 107
b. 5,23 × 10-6
4. a. 3 578
b. 0,000043
II
7
Représentation graphique d’une équation linéaire
Les équations dont les graphiques sont des lignes droites sont appelées équations linéaires. Voici quelques exemples d’équations linéaires :
Une droite est entièrement déterminée par deux points. Par conséquent, pour représenter graphiquement une équation linéaire, nous devons trouver les coordonnées de ces deux points. Pour ce faire, nous choisissons une valeur arbitraire pour x ou y, puis nous résolvons l’équation pour l’autre variable.
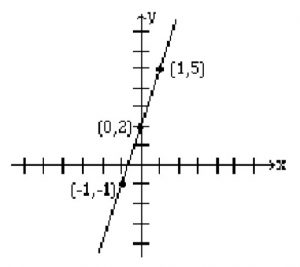
Représentation graphique de la droite : y = 3x + 2
Solution
Nous devons trouver les coordonnées d’au moins deux points.
Nous choisissons arbitrairement x = -1, x = 0, et x = 1.
Si x = -1, alors y = 3(-1) + 2 ou -1. Par conséquent, (-1, -1) est un point sur cette droite.
Si x = 0, alors y = 3(0) + 2 ou y = 2, d’où le point (0, 2).
Si x = 1, alors y = 5, et nous obtenons le point (1, 5). Les résultats sont résumés ci-dessous et la ligne est représentée sous forme de graphique.
| X | -1 | 0 | 1 |
| Y | -1 | 2 | 5 |
Si y = 2, alors 2x + 2 = 4, ce qui donne x = 1 et le point (1, 2). Le tableau ci-dessous indique les points, et la droite est représentée sous forme de graphique.
| x | -1 | 0 | 1 |
| y | 6 | 4 | 2 |
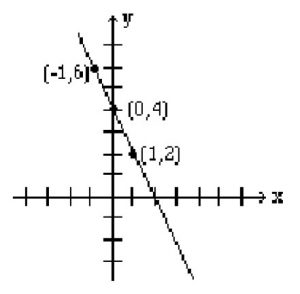
Les points où une ligne croise l’axe des coordonnées sont appelés points d’interception. Lorsqu’on représente une ligne sous forme de graphique, on commence généralement par les points d’intersection, car ils sont faciles à trouver. Pour trouver l’abscisse à l’origine, on met y = 0, et pour trouver l’ordonnée à l’origine, on met x = 0.
Les résultats sont présentés dans le tableau ci-dessous.
| t | 0 | 1 | 2 |
| x | 3 | 5 | 7 |
| y | 1 | 2 | 3 |
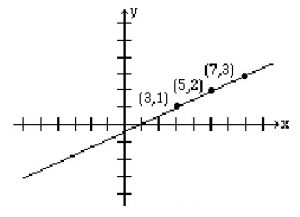
Lorsque l’équation d’une droite n’a qu’une seule variable, le graphique résultant est une droite horizontale ou verticale.
Le graphique de la droite x = a (a étant une constante) est une droite verticale qui passe par le point (a , 0). Tout point de cette droite a pour coordonnée x a , quelle que soit la coordonnée y.
Le graphique de la droite y = b (b étant une constante) est une droite horizontale qui passe par le point (0, b). Tout point de cette droite a pour coordonnée y b , quelle que soit la coordonnée x.
Remarque : La plupart des étudiants pensent que les coordonnées des points doivent toujours être des nombres entiers. Ce n’est pas vrai et, en réalité, ce n’est pas toujours possible. Ne vous inquiétez pas si vos points comprennent des fractions ou des décimales.
1. Le point (2, 3) est-il situé sur la droite 5x – 2y = 4?
2. Pour la droite 3x – y = 12, complétez les coordonnées suivantes :
3. Représentez sous forme de graphique y = 4x – 3.
4. Représentez sous forme de graphique 2x + 4 = 0.
5. Représentez graphiquement la droite donnée par les équations paramétriques x = 1 + 2t et y = 3 + t.
6. Représentez graphiquement les trois équations suivantes sur le même ensemble d’axes des coordonnées : y = x + 1; y = 2x + 1; y = –x + 1.
8
Dans cette section, vous apprendrez à :
Dans la dernière section, nous avons appris à représenter graphiquement une droite à partir de deux points. Il est également possible de dessiner graphiquement une droite en connaissant un point et la « pente » de cette droite. La pente d’une droite est un nombre précis qui exprime son inclinaison.
Vous vous souvenez peut-être d’avoir vu, dans un cours de mathématiques précédent, que la pente est « l’inclinaison de la droite » ou « la variation verticale par rapport à la variation horizontale » et qu’elle est souvent exprimée des façons suivantes :
Nous vous en donnons ici une définition plus précise.
Définition :
Si ( x1, y1) et ( x2, y2) sont deux points différents sur une droite, alors la pente de la droite est ![]()
La variation verticale (-4) et la variation horizontale (6) sont toutes deux indiquées dans la figure ci-dessus.
Lorsque deux points sont donnés, il importe peu de savoir quel point est désigné par (x1, y1) et quel point est désigné par (x2, y2). La valeur de la pente sera la même. Par exemple, si nous choisissons (x1, y2) = (4, -1) et (x2, y2) = (-2, 3), nous obtiendrons la même valeur pour la pente que celle obtenue précédemment. Les étapes à effectuer sont les suivantes :
L’étudiant doit également comprendre le point suivant : si une droite monte de gauche à droite, elle a une pente positive; si elle descend de gauche à droite, elle a une pente négative.
Alternativement, puisque ![]() représente le même nombre, la droite peut être tracée en commençant au point (1, 2) et en choisissant une variation verticale de 3 unités suivie d’une variation horizontale de 4 unités. Ainsi, à partir du point (1, 2), nous montons de 3 unités, et nous nous déplaçons à gauche de 4 unités, atteignant le point (-3, 5) qui est également sur la même droite. Voir la figure ci-dessous.
représente le même nombre, la droite peut être tracée en commençant au point (1, 2) et en choisissant une variation verticale de 3 unités suivie d’une variation horizontale de 4 unités. Ainsi, à partir du point (1, 2), nous montons de 3 unités, et nous nous déplaçons à gauche de 4 unités, atteignant le point (-3, 5) qui est également sur la même droite. Voir la figure ci-dessous.
Prenons les pentes et les ordonnées à l’origine des droites suivantes.
| Droite | Pente | Ordonnée à l’origine |
| y = 3x + 2 | 3 | 2 |
| y = -2x + 5 | -2 | 5 |
| y = 3/2x – 4 | 3/2 | -4 |
Ce n’est pas une coïncidence : lorsque l’équation d’une droite est résolue pour y, le coefficient du terme x correspond à la pente et la constante correspond à l’ordonnée à l’origine.
En d’autres mots, dans la droite y = mx + b, m est la pente et b est l’ordonnée à l’origine.
Déterminer la pente et l’ordonnée à l’origine de la droite 2x + 3y = 6.
Solution
1. Trouvez la pente de la droite qui traverse les coordonnées suivantes.
2. Déterminez la pente à partir de l’équation de la droite :
3. Représentez graphiquement la droite qui passe par le point donné et qui a la pente donnée.
9
Dans cette section, vous apprendrez à :
Jusqu’ici, nous avons trouvé des informations à partir de l’équation d’une droite. Nous avons notamment trouvé des points sur la droite, la pente et les points d’intersection. Nous allons à présent faire le contraire : nous allons trouver l’équation de la droite à partir de deux de ses points, ou à partir d’un point et de la pente.
L’équation d’une droite peut être écrite sous deux formes : la forme canonique ou la forme standard.
Forme canonique : y = mx + b
Une droite est entièrement déterminée par deux points, ou par un point et une pente. Il est donc possible de trouver l’équation d’une droite si l’une de ces deux situations est donnée.
Trouver la forme standard de la droite qui passe par les points (1, -2) et (4, 0).
Solution
Voici la forme point-pente de l’équation :
En multipliant les deux côtés par 3, on obtient :
Nous devrions toujours être en mesure de convertir une forme d’équation en une autre. En d’autres termes, si nous avons une droite exprimée sous forme canonique, nous devrions pouvoir l’exprimer sous la forme standard, et vice versa.
Écrire l’équation y = –2/3x + 3 sous la forme standard.
Solution
En multipliant les deux côtés de l’équation par 3, on obtient :
Pour finir, nous allons voir une méthode très rapide et facile pour écrire l’équation d’une droite sous la forme standard. Mais nous devons d’abord apprendre à trouver la pente d’une droite sous la forme standard par l’inspection.
En recherchant la valeur de y, nous pouvons facilement montrer que la pente de la droite Ax + By = C est −A/B. Il est important de vérifier ce résultat.
Maintenant que nous savons comment trouver la pente d’une droite sous la forme standard par l’inspection, il est très facile de trouver l’équation.
1. Inscrivez l’équation de la droite pour chacun des cas suivants. Utilisez la forme y = mx + b.
2. Inscrivez l’équation de la droite pour chacun des cas suivants. Utilisez la forme Ax + By = C.
10
Maintenant que nous avons appris à déterminer l’équation d’une droite, nous pouvons appliquer ce principe à des situations de la vie réelle.
Dans le problème ci-dessus, 0,50 $ par kilomètre est un coût variable, tandis que le montant forfaitaire de 5 $ est un coût fixe. Si nous examinons maintenant notre équation y = 0,50x + 5, nous constatons que le coût variable correspond à la pente et le coût fixe, à l’ordonnée à l’origine.
Le coût variable de fabrication d’un produit est de 10 $ et le coût fixe est de 2 500 $. Si x représente le nombre d’articles fabriqués et y le coût total, écrivez la fonction du coût.
Solution
Le coût variable correspond à la pente et le coût fixe correspond à l’ordonnée à l’origine. Donc, m = 10 et y = 2 500.
L’équation du coût est y = 10x + 2 500.
La fabrication de 25 articles coûte 750 $ et celle de 50 articles coûte 1 000 $. En supposant qu’une relation linéaire existe, trouvez l’équation de coût et utilisez cette fonction pour prévoir le coût de 100 articles.
Solution
Soit x = le nombre d’articles fabriqués, et y = le coût.
Résoudre ce problème revient à trouver l’équation d’une droite qui passe par les points (25, 750) et (50, 1 000).
L’équation partielle est donc y = 10x + b.
En intégrant l’un des points à l’équation, nous obtenons b = 500.
L’équation du coût est donc y = 10x + 500.
Pour trouver le coût de 100 articles, nous remplaçons x par 100 dans l’équation y = 10x + 500.
Le coût = y = 10(100) + 500 = 1 500.
Examinons l’énoncé.
| Celsius | Fahrenheit |
| 0 | 32 |
| 100 | 212 |
Là encore, résoudre ce problème revient à trouver l’équation d’une droite qui passe par les points (0, 32) et (100, 212).
Comme il s’agit d’une relation linéaire, nous recherchons une équation y = mx + b, ou dans ce cas F = mC+ b, où x ou C représente la température en degrés Celsius, et y ou F représente la température en degrés Fahrenheit.
L’équation est ![]()
En utilisant le point (0, 32), nous obtenons :
Pour convertir 30 degrés Celsius en degrés Fahrenheit, nous remplaçons C = 30 par l’équation suivante :
La population du Canada était de 18 millions d’habitants en 1970 et de 26 millions en 1986. En supposant que la croissance de la population est linéaire, et que x représente l’année et y la population, écrivez la fonction qui explique la relation entre le temps et la population. Utilisez cette équation pour prédire la population du Canada en 2010.
Solution
Le problème peut être facilité en utilisant 1970 comme année de base, c’est-à-dire en choisissant l’année 1970 comme année zéro. Cela signifie que l’année 1986 correspondra à l’année 16, et l’année 2010 à l’année 40.
Examinons maintenant les informations dont nous disposons.
Résoudre ce problème revient à trouver l’équation d’une droite qui passe par les points (0, 18) et (16, 26).
L’équation est ![]() .
.
En utilisant le point (0, 18), nous obtenons :
Pour trouver la population en 2010, nous supposons que x = 40 dans l’équation :
La population du Canada en 2010 est donc estimée à 38 millions d’habitants.
| Année | Population |
| 0 (1970) | 18 millions |
| 16 (1986) | 26 millions |
Dans cette section, vous apprendrez à :
Dans cette section, nous résoudrons des problèmes qui impliquent l’intersection de deux droites. Par conséquent, avant d’aller plus loin, nous allons d’abord apprendre à trouver cette intersection.
Trouver l’intersection de la droite y = 3x − 1 et de la droite y = −x + 7.
Solution
Nous représentons les deux droites sur les mêmes axes, comme indiqué ci-dessous, et arrivons à la solution (2, 5).
Trouver graphiquement l’intersection de deux droites n’est pas toujours facile ou pratique; c’est pourquoi nous allons maintenant apprendre à résoudre ces problèmes de manière algébrique.
Au point d’intersection de deux droites, les valeurs x et y des deux droites sont identiques. Pour trouver l’intersection, il faut donc que les valeurs x ou les valeurs y soient égales.
Si nous devions résoudre l’exemple ci-dessus de manière algébrique, il serait plus facile de laisser les valeurs de y égales. Puisque y = 3x − 1 pour la première droite, et y = −x + 7 pour la deuxième droite, en laissant les valeurs de y égales, nous obtenons :
En remplaçant x = 2 dans l’une des deux équations, nous obtenons y = 5, d’où la solution (2, 5).
La méthode d’élimination (ou méthode de réduction) est une méthode algébrique couramment utilisée pour résoudre les systèmes d’équations. Elle vise à éliminer l’une des deux variables en additionnant les côtés gauche et droit des équations. Une fois qu’une variable est éliminée, nous obtenons une équation à variable unique dont il est possible de trouver la valeur. Enfin, en remplaçant la valeur de la variable trouvée dans l’une des équations initiales, nous pouvons trouver la valeur de l’autre variable. La méthode est démontrée dans l’exemple ci-dessous.
Résoudre le système d’équations x + 2y = 3 et 2x + 3y = 4 par la méthode d’élimination.
Solution
Si nous additionnons les deux équations, aucune des variables n’est éliminée. Or, la variable x peut être éliminée en multipliant la première équation par -2 et en laissant la deuxième équation inchangée.
En utilisant y = 2 dans x + 2y = 3, nous obtenons :
La solution est donc (-1, 2).
Résoudre le système d’équations 3x − 4y = 5 et 4x − 5y = 6.
Solution
Dans une économie de marché, la courbe d’offre correspond au nombre d’articles qui peuvent être mis à disposition à différents prix, et la courbe de demande est le nombre d’articles que le consommateur achètera à différents prix. Lorsque le prix d’un produit augmente, la demande diminue et l’offre augmente. En revanche, lorsque le prix diminue, la demande augmente et l’offre diminue. Le prix d’équilibre est atteint lorsque la demande est égale à l’offre.
1. Le coût variable de fabrication d’un article est de 20 $ et la production de 20 articles coûte au total 750 $. Si x représente le nombre d’articles fabriqués et y le coût, écrivez la fonction du coût.
2. Une personne qui pèse 150 kilos a 60 kilos de muscles, et une personne qui pèse 180 kilos a 72 kilos de muscles. Si x représente la masse corporelle et y la masse musculaire, écrivez une équation décrivant leur relation. Utilisez cette relation pour déterminer la masse musculaire d’une personne qui pèse 170 kilos.
3. Une maison moyenne dans la région du Grand Toronto coûtait 335 907 $ en 2005 et 787 300 $ en 2018. En supposant une relation linéaire, prévoyez le prix d’une maison similaire en 2025.
4. En 2010, on a signalé 11 386 cas de gonorrhée confirmés en laboratoire au Canada. En 2015, ce nombre est passé à 19 845. En supposant une relation linéaire, à combien de cas de gonorrhée peut-on s’attendre en 2030?
5. La courbe d’offre d’un produit est y = 2 000x + 13 000, et la courbe de demande est y = -1 000x + 28 000, où x représente le prix et y le nombre d’articles. À quel prix l’offre sera-t-elle égale à la demande et combien d’articles seront produits à ce prix?
6. Une entreprise qui produit des jouets a des coûts fixes de 10 725 $ et des coûts variables de 20 cents par jouet. Trouvez le seuil de rentabilité si les jouets se vendent à 1,50 $ l’unité.
11
1. Oui
2. a. (2, -6) (6, 6)
3.
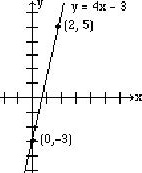
4.
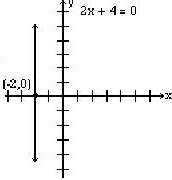
5.
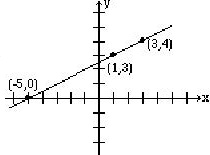
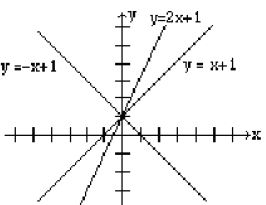
1. a. m = 2
b. m = -2
c. m = -1
2. a. m = -2
b. m = ![]()
c. m = 2
3. a.
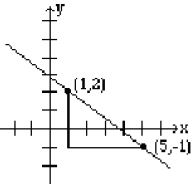
3. b.
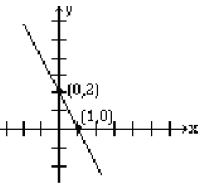
1. a. ![]()
b. ![]()
c. ![]()
d. ![]()
e. ![]()
f. ![]()
2. a. ![]()
b. ![]()
1. ![]()
2. ![]() ,
, ![]() livres
livres
3. ≈ 1 030 358 $
4. 45 222
5. ![]() $,
$, ![]() articles
articles
6. (8 250, 12 375)
III
12
Le monde qui nous entoure est rempli de relations entre différentes variables qui changent. Lorsque nous observons ces relations, il est normal de se demander : « Si je connais une variable, puis-je déterminer l’autre? ». Cela établit l’idée d’une variable d’entrée, ou variable indépendante, et d’une variable de sortie correspondante, ou variable dépendante. De là découle la notion de relation fonctionnelle dans laquelle la valeur de sortie peut être déterminée à partir de la valeur d’entrée.
Parfois, il existe des relations entre certaines variables, comme la taille et l’âge, par exemple. En effet, pour une personne donnée à un âge donné, il est assez facile de déterminer sa taille, mais si nous inversions cette relation et que nous essayions de déterminer l’âge d’une personne à partir de sa taille, cela serait plus difficile, car la plupart des gens conservent la même taille pendant de nombreuses années.
Dans l’exemple de la taille et de l’âge ci-dessus, la taille est-elle une fonction de l’âge? L’âge est-il une fonction de la taille?
Ici, il serait exact de dire que la taille est une fonction de l’âge, puisque chaque âge détermine de manière unique une taille. Par exemple, le jour de mon 18e anniversaire, j’avais une taille de précisément 69 pouces.
Cependant, l’âge n’est pas une fonction de la taille, car une taille (variable d’entrée, ou indépendante) peut correspondre à plus d’un âge (variable de sortie, ou dépendante). Par exemple, pour une taille de 70 pouces (variable indépendante), il y a plus d’un âge possible (variable dépendante) puisque je mesurais 70 pouces à l’âge de 20 et de 21 ans.
Dans un café, le menu se compose de différents choix et de leur prix. Le prix est-il une fonction du choix? Le choix est-il une fonction du prix?
Nous pourrions dire que le prix est une fonction du choix, puisque chaque choix (variable indépendante) a un prix qui lui correspond (variable dépendante). Nous ne pouvons pas dire que le choix est une fonction du prix, puisque deux choix peuvent avoir le même prix.
Dans de nombreux cours, le pourcentage global que vous obtenez correspond à une note décimale. La note décimale est-elle une fonction du pourcentage? Le pourcentage est-il une fonction de la note décimale?
Tout pourcentage obtenu est associé à une note décimale. Nous pouvons donc dire que la note décimale est une fonction du pourcentage. Autrement dit, si vous entrez un pourcentage, vous obtiendrez une valeur décimale. Le pourcentage peut ou non être une fonction de la note décimale, selon le système de notation du personne enseignant. Dans certains systèmes de notation, il existe une gamme de pourcentages correspondant à la même note décimale.
Pour simplifier l’écriture des expressions et des équations impliquant des fonctions, on utilise souvent une notation simplifiée. Nous utilisons également des variables descriptives pour nous aider à nous souvenir de la signification des quantités dans le problème.
Plutôt que d’écrire « la taille (hauteur) est une fonction de l’âge », nous pourrions utiliser la variable descriptive h pour représenter la taille et la variable descriptive a pour représenter l’âge.
| « la taille est une fonction de l’âge » | Si nous nommons la fonction f, nous écrivons |
| « h est f de a » | ou plus simplement |
| h = f(a). | Nous pourrions aussi nommer la fonction h et écrire |
| h(a) | qui se lit « h de a ». |
Rappelez-vous que nous pouvons utiliser n’importe quelle variable pour nommer la fonction; la notation h(a) nous indique que h dépend de a. La valeur « a » doit être introduite dans la fonction « h » pour obtenir un résultat. Attention : Les parenthèses indiquent que l’âge est introduit dans la fonction (il ne faut pas confondre ces parenthèses avec la multiplication!).
Introduisez la notation fonctionnelle pour représenter une fonction qui prend en entrée le nom d’un mois et donne en sortie le nombre de jours de ce mois.
Le nombre de jours dans un mois est une fonction du nom du mois, donc si nous nommons la fonction f, nous pourrions écrire « jours = f(mois) » ou j = f(m). Si nous nommons simplement la fonction d, nous pourrions écrire j(m).
Par exemple, j(mars) = 31, puisque le mois de mars compte 31 jours. La notation j(m) nous rappelle que le nombre de jours, j (la sortie) dépend du nom du mois, m (l’entrée).
Une fonction N = f(y) indique le nombre de policiers, N, dans une ville au cours de l’année y. Que nous apprend f(2005) = 300?
Lorsque nous lisons f(2005) = 300, nous voyons que la valeur d’entrée de la fonction est 2005, soit l’année (y). La valeur de sortie est 300, soit le nombre de policiers (N), une quantité. Rappelez-vous que N = f(y). Cela signifie donc qu’en 2005, il y avait 300 policiers dans la ville.
Les fonctions peuvent être représentées de différentes manières : des mots (comme dans les derniers exemples), des tableaux de valeurs, des graphiques ou des formules. Dans le cas d’un tableau, on nous présente une liste de valeurs d’entrée et de sortie.
Dans certains cas, ces valeurs représentent tout ce que nous savons sur la relation, alors que dans d’autres cas, le tableau fournit simplement certaines valeurs d’une relation plus complète.
Tableau 3.1.1 : Ce tableau représente en entrée le numéro du mois (janvier = 1, février = 2, etc.) et en sortie le nombre de jours de ce mois. Cela désigne tout ce que nous savons sur les mois et les jours pour une année donnée (qui n’est pas une année bissextile).
| (entrée) numéro du mois, m | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
| (sortie) nombre de jours du mois, j | 31 | 28 | 31 | 30 | 31 | 30 | 31 | 31 | 30 | 31 | 30 | 31 |
Tableau 3.1.2 : Le tableau ci-dessous définit une fonction Q = g(n). Rappelez-vous que cette notation nous indique que g est le nom de la fonction qui prend l’entrée n et donne la sortie Q.
| n | 1 | 2 | 3 | 4 | 5 |
| Q | 8 | 6 | 7 | 6 | 8 |
Tableau 3.1.3 : Ce tableau représente l’âge des enfants en années et leur taille correspondante. Il ne s’agit là que d’une partie des données disponibles sur la taille et l’âge des enfants.
| (entrée) a, âge en années | 5 | 5 | 6 | 7 | 8 | 9 | 10 |
| (sortie) h, taille (hauteur) en pouces | 40 | 42 | 44 | 47 | 50 | 52 | 54 |
Lequel de ces tableaux définit une fonction (le cas échéant)?
| Entrée | Sortie | Entrée | Sortie | Entrée | Sortie |
| 2 | 1 | -3 | 5 | 1 | 0 |
| 5 | 3 | 0 | 1 | 5 | 2 |
| 8 | 6 | 4 | 5 | 5 | 4 |
Le premier et le deuxième tableau définissent des fonctions. Dans les deux cas, chaque entrée correspond à exactement une seule sortie. Le troisième tableau ne définit pas une fonction puisque la valeur d’entrée de 5 correspond à deux valeurs de sortie différentes.
Lorsque nous travaillons avec des fonctions, nous faisons généralement deux choses : évaluer et résoudre. Nous faisons l’évaluation d’une fonction lorsque nous connaissons une valeur d’entrée et que nous utilisons la fonction pour déterminer la valeur de sortie correspondante. Elle produira toujours un seul résultat, puisque chaque entrée d’une fonction correspond à exactement une seule sortie.
Nous faisons la résolution d’équations impliquant une fonction lorsque nous connaissons une valeur de sortie et que nous utilisons la fonction pour déterminer les valeurs d’entrée qui produiraient cette valeur de sortie. La résolution d’une fonction peut produire plus d’une solution, puisque des entrées différentes peuvent produire la même sortie.
En utilisant le tableau présenté, où Q = g(n)
| n | 1 | 2 | 3 | 4 | 5 |
| Q | 8 | 6 | 7 | 6 | 8 |
a) Évaluez g(3).
Évaluer g(3) (lire « g de 3 ») signifie que nous devons déterminer la valeur de sortie, Q, de la fonction g en fonction de la valeur d’entrée n = 3. En regardant le tableau, nous voyons que la valeur de sortie correspondant à n = 3 est Q = 7, ce qui nous permet de conclure que g(3) = 7.
b) Résolvez g(n) = 6.
Résoudre g(n) = 6 signifie que nous devons déterminer quelles valeurs d’entrée, n, produisent une valeur de sortie de 6. En regardant le tableau, nous voyons qu’il y a deux solutions : n = 2 et n = 4.
Lorsque nous entrons 2 dans la fonction g, notre résultat est Q = 6.
Lorsque nous entrons 4 dans la fonction g, notre résultat est aussi Q = 6.
Souvent, le graphique d’une relation peut être utilisé pour définir une fonction. Par convention, les graphiques sont généralement créés avec la valeur d’entrée (variable indépendante) le long de l’axe horizontal, et la valeur de sortie (variable dépendante) le long de l’axe vertical.
Le graphique le plus courant présente y sur l’axe vertical et x sur l’axe horizontal, et nous disons que y est une fonction de x, ou y = f(x) lorsque la fonction s’appelle f.
Lequel de ces graphiques définit une fonction y = f(x)?
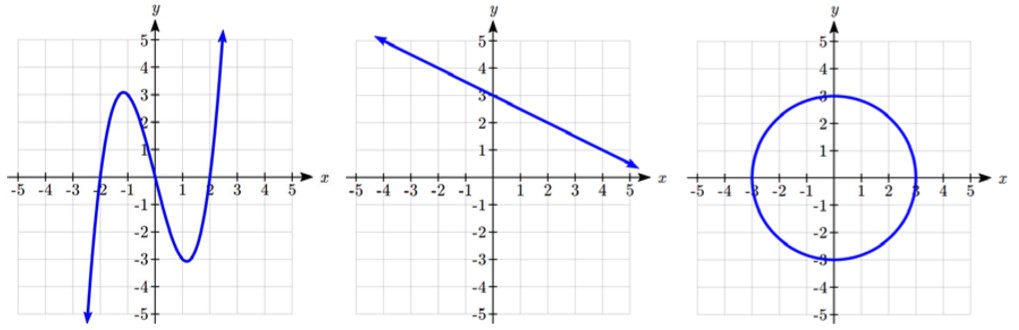
Si l’on examine les trois graphiques ci-dessus, les deux premiers définissent une fonction y = f(x), puisque chaque valeur d’entrée sur l’axe horizontal correspond exactement à une seule valeur de sortie, déterminée par la valeur y du graphique. Le troisième graphique ne définit pas une fonction y = f(x) puisque certaines valeurs d’entrée, telles que x = 2, correspondent à plus d’une valeur de sortie.
L’évaluation d’une fonction à l’aide d’un graphique consiste à prendre l’entrée donnée et à utiliser le graphique pour trouver la sortie correspondante, alors que la résolution d’une fonction à l’aide d’un graphique consiste à prendre la sortie donnée et à utiliser le graphique pour trouver l’entrée correspondante.
À l’aide du graphique ci-dessous :
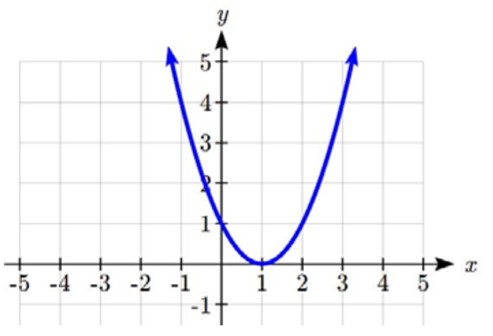
a) Évaluez f(2).
b) Résolvez f(x) = 4.
Solution
a) Pour évaluer f(2), nous trouvons l’entrée de x = 2 sur l’axe horizontal. En se déplaçant vers le haut du graphique, on obtient le point (2, 1), ce qui donne la sortie y = 1. Donc, f(2) = 1.
b) Pour résoudre f(x) = 4, nous trouvons la valeur 4 sur l’axe vertical, car si f(x) = 4, 4 est la sortie. En se déplaçant horizontalement sur le graphique, on obtient deux points avec une sortie de 4 : (-1, 4) et (3, 4). Ce sont donc les deux solutions de f(x) = 4 : x = -1 ou x = 3. Cela signifie que f(-1) = 4 et f(3) = 4, ou lorsque l’entrée est -1 ou 3, la sortie est 4.
Lorsque cela est possible, il est très pratique de définir les relations à l’aide de formules. S’il est possible d’exprimer la sortie sous la forme d’une formule impliquant la quantité de l’entrée, nous pouvons alors définir une fonction.
Exprimez la relation 2n + 6p = 12 sous la forme d’une fonction p = f(n) si possible.
Pour exprimer la relation sous cette forme, nous devons être en mesure d’écrire la relation où p est une fonction de n, ce qui signifie l’écrire sous la forme p = [quelque chose impliquant n].
![]() Soustrayez 2n des deux côtés.
Soustrayez 2n des deux côtés.
![]() Divisez les deux côtés par 6 et simplifiez l’écriture.
Divisez les deux côtés par 6 et simplifiez l’écriture.
![]()
Après avoir réécrit la formule p =, nous pouvons exprimer p comme une fonction : ![]() ..
..
Il est important de noter que ce ne sont pas toutes les relations qui peuvent être exprimées sous la forme d’une formule.
La caractéristique la plus importante d’une équation écrite sous forme de fonction est que la valeur de sortie peut être déterminée directement à partir de la valeur d’entrée au moyen d’évaluations; aucune autre résolution n’est nécessaire. Cela permet à la relation d’agir comme une boîte magique qui prend une valeur d’entrée, la traite, et renvoie une valeur de sortie. La technologie moderne et les ordinateurs s’appuient sur ces relations fonctionnelles, car l’évaluation de la fonction peut être programmée dans les machines, alors que la résolution est beaucoup plus complexe.
Comme pour les tableaux et les graphiques, il est courant d’évaluer et de résoudre des fonctions impliquant des formules. L’évaluation consiste à remplacer la variable d’entrée de la formule par la valeur fournie, puis à faire le calcul. Pour la résolution, il faut remplacer la variable de sortie de la formule par la valeur fournie, puis trouver la ou les valeurs d’entrée qui produiraient cette valeur de sortie.
À l’aide de la fonction k(t) = t3 + 2 :
a) Évaluez k(2).
b) Résolvez k(t) = 1.
Solution
a) Pour évaluer k(2), nous introduisons la valeur d’entrée 2 dans la formule chaque fois que nous voyons la variable d’entrée t, puis nous simplifions l’écriture.
k(2) = 23 + 2
k(2) = 8 + 2
Donc, k(2) = 10.
b) Pour résoudre k(t) = 1, nous définissons la formule pour k(t) = 1, et nous résolvons la valeur d’entrée qui produira cette valeur de sortie.
k(t) = 1 Remplacez la formule d’origine. k(t) = t3 + 2
t3 + 2 = 1 Soustrayez 2 de chaque côté.
t3 = -1 Enlevez la racine cubique de chaque côté.
t = -1
Lorsque vous résolvez une équation à l’aide de formules, vous pouvez vérifier votre réponse en utilisant votre solution dans l’équation originale pour voir si votre réponse calculée est exacte.
Par exemple, nous voulons savoir si k(t) = 1 est vrai lorsque t = -1.
k(-1) = (-1)3 + 2
À l’aide de la fonction h(p) = p2 + 2p :
a) Évaluez h(4).
b) Résolvez h(p) = 3.
Solution
Pour évaluer h(4), nous remplaçons la valeur 4 par la variable d’entrée p dans la fonction donnée.
a) h(4) = (4)2 + 2(4)
b) h(p) = 3 Remplacez la fonction originale h(p) = p2 + 2p.
p2 + 2p = 3 Comme il s’agit d’une fonction quadratique, nous pouvons réarranger l’équation pour obtenir 0.
p2 + 2p – 3 = 0 Soustrayez 3 de chaque côté.
p2 + 2p – 3 = 0 Cette équation peut être factorisée, ce que nous faisons.
(p + 3)(p – 1) = 0
Par le théorème du facteur zéro, puisque (p + 3)(p – 1) = 0, soit (p + 3) = 0, soit (p – 1) = 0 (ou les deux équations sont égales à 0). Nous résolvons donc les deux équations pour p, en trouvant p = -3 dans la première équation et p = 1 dans la seconde.
Cela nous donne la solution : h(p) = 3 lorsque p = 1 ou p = -3.
1. Votre solde est-il une fonction de votre numéro de compte bancaire? (Si vous entrez un numéro de compte bancaire, est-il logique que le résultat soit votre solde?)
2. Votre numéro de compte bancaire est-il une fonction de votre solde? (Si vous entrez un solde, est-il logique que le résultat soit votre numéro de compte bancaire?)
3. Si chaque pourcentage obtenu se traduisait par une note en lettres, s’agirait-il d’une fonction?
4. En utilisant la fonction de l’exemple 3.1.7, évaluez g(4).
5. En utilisant le graphique de l’exemple 3.1.9, résolvezf(x) = 1.
6. À l’aide de la fonction ![]() :
:
13
L’un des principaux objectifs des mathématiques est de modéliser le monde réel à l’aide de fonctions mathématiques. À cet effet, il est important de garder à l’esprit les limites des modèles que nous créons.
Ce tableau montre la relation entre la circonférence et la hauteur d’un arbre au cours de sa croissance.
| Circonférence (c) | 1,7 | 2,5 | 5,5 | 8,2 | 13,7 |
| Hauteur (h) | 24,5 | 31 | 45,2 | 54,6 | 92,1 |
Bien qu’il existe un lien étroit entre les deux, il serait certainement insensé de parler d’un arbre d’une circonférence de -3 pieds ou d’une hauteur de 3 000 pieds. Lorsque nous définissons les limites des valeurs d’entrée et de sortie d’une fonction, nous déterminons le domaine et l’étendue de cette fonction.
À l’aide du tableau ci-dessus, déterminez un domaine et une étendue raisonnables.
Nous pourrions combiner les données fournies avec nos propres expériences et notre raisonnement pour estimer le domaine et l’étendue de la fonction h = f(c). Pour le domaine, les valeurs possibles de la circonférence (entrée), c, il n’est pas logique d’avoir des valeurs négatives, donc c > 0. Nous pourrions supposer une valeur maximale raisonnable, et estimer que la circonférence maximale est d’environ 119 pieds. Nous pourrions donc dire qu’un domaine raisonnable serait 0 < c ≤ 119 pieds.
De même, pour l’étendue, il n’est pas logique que la hauteur soit négative, et la hauteur maximale d’un arbre pourrait être de 379 pieds, de sorte qu’une étendue raisonnable pourrait être 0 < h ≤ 379 pieds.
Lors de l’envoi d’une lettre par le service postal des États-Unis, le prix dépend du poids de la lettre, comme le montre le tableau ci-dessous. Déterminez le domaine et l’étendue.
| Lettres | |
| Poids ne dépassant pas | Prix |
| 1 once | 0,44 $ |
| 2 onces | 0,61 $ |
| 3 onces | 0,78 $ |
| 3,5 onces | 0,95 $ |
Supposons que nous notons le poids avec w et le prix avec p, et que nous créons une fonction appelée P, où le prix, p, est une fonction du poids, w. Donc p = P(w).
Puisque les poids acceptés sont de 3,5 onces ou moins, et que les poids négatifs ne sont pas logiques ici, le domaine serait 0 < w ≤ 3,5. Techniquement, le 0 pourrait être inclus dans le domaine, mais logiquement, cela signifierait que nous n’envoyons rien, donc nous pouvons l’ignorer.
Puisque les prix possibles font partie d’un ensemble limité de valeurs, nous ne pouvons définir l’étendue de cette fonction qu’en énumérant les valeurs possibles. L’étendue est donc p = 0,44 $, 0,61 $, 0,78 $ ou 0,95 $.
Dans les exemples précédents, nous avons utilisé des inégalités pour décrire le domaine et l’étendue des fonctions. C’est l’une des façons de décrire les intervalles des valeurs d’entrée et de sortie, mais ce n’est pas la seule.
L’utilisation d’inégalités, telles que 0 < c ≤ 163, 0 < w ≤ 3,5 et 0 < h ≤ 379, implique que nous nous intéressons à toutes les valeurs comprises entre les valeurs inférieures et les supérieures, y compris les valeurs supérieures dans ces exemples.
Cependant, il arrive que nous nous intéressions à une liste précise de nombres, comme l’étendue de prix pour l’envoi de lettres, p = 0,44 $, 0,61 $, 0,78 $ ou 0,95 $. Ces nombres représentent un ensemble de valeurs précises : {0,44; 0,61; 0,78; 0,95}.
Le fait de représenter des valeurs sous la forme d’un ensemble, ou de donner des instructions sur la manière dont un ensemble est construit, nous amène à utiliser un autre type de notation pour décrire le domaine et l’étendue. Supposons que nous voulons décrire les valeurs d’une variable x qui sont supérieures ou égales à 10, mais inférieures à 30. Dans les inégalités, nous écririons 10 ≤ x < 30.
Lorsque nous décrivons des domaines et des étendues, nous étendons parfois cette notation à la compréhension, qui ressemblerait à ce qui suit : {x | 10 ≤ x < 30}. Les accolades { } se lisent comme « l’ensemble de », et la barre verticale | se lit comme « tel que », de sorte que nous lirions {x | 10 ≤ x < 30} comme « l’ensemble des valeurs x telles que 10 est inférieur ou égal à x, et x est inférieur à 30 ».
Lorsque l’on décrit des étendues en compréhension, on peut écrire quelque chose comme {f(x) | 0 < f(x) < 100}, ou si la sortie a sa propre variable, on peut l’utiliser. Ainsi, pour notre exemple ci-dessus de la hauteur d’arbre, nous pourrions écrire pour l’étendue : {h | 0 < h ≤ 379}. Dans la notation en compréhension, si une étendue ou un domaine n’est pas limité, nous pourrions écrire {t | t est un nombre réel}, ou {t | t ∈ ℜ}, c’est-à-dire « l’ensemble des valeurs t telles que t est un élément de l’ensemble des nombres réels ».
Une variante simplifiée de la notation en compréhension est la notation en intervalle, où les intervalles de valeurs sont désignés par les valeurs de départ et d’arrivée. Des parenthèses courbes sont utilisées pour « strictement inférieur à », et des crochets pour « inférieur ou égal à ». L’infini n’étant pas un nombre, nous ne pouvons pas l’inclure dans l’intervalle, c’est pourquoi nous utilisons toujours des parenthèses courbes avec ∞ et -∞. Le tableau ci-dessous vous aidera à comprendre comment les inégalités correspondent à la notation en compréhension et à la notation en intervalle :
| Inégalités | Notation en compréhension | Notation en intervalle |
| 5 < h ≤ 10 | {h | 5 < h ≤ 10} | (5, 10] |
| 5 ≤ h < 10 | {h | 5 ≤ h < 10} | [5, 10) |
| 5 < h ≤ 10 | {h | 5 < h < 10} | (5, 10) |
| h < 10 | {h | h < 10} | (-∞, 10) |
| h ≥ 10 | {h | h ≥ 10} | [10, ∞) |
| Tous les nombres réels | {h | h ∈ ℜ} | (-∞, ∞) |
Pour combiner deux intervalles en utilisant des inégalités ou la notation en compréhension, nous pouvons utiliser le mot « ou ». Dans la notation en intervalle, nous utilisons le symbole d’union ∪ pour combiner deux intervalles non connectés.
Décrivez les intervalles de valeurs représentés sur le graphique linéaire ci-dessous en utilisant la notation en compréhension et en intervalle.
Pour décrire les valeurs, x, qui se trouvent dans les intervalles indiqués ci-dessus, nous dirions : « x est un nombre réel supérieur ou égal à 1, et inférieur ou égal à 3, ou un nombre réel supérieur à 5 ».
Avec une inégalité, on écrirait : 1 ≤ x ≤ 3 ou x > 5
Avec une notation en compréhension : {x | 1 ≤ x ≤ 3 ou x > 5}
Avec une notation en intervalle : [1, 3] ∪ (5, ∞)
N’oubliez pas, lorsque vous écrivez ou lisez une notation en intervalle, l’utilisation d’un crochet [ signifie que la valeur de départ est incluse dans l’ensemble, et l’utilisation d’une parenthèse ( que la valeur de départ n’est pas incluse dans l’ensemble.
Nous pouvons également parler de domaine et d’étendue en nous basant sur des graphiques. Étant donné que le domaine fait référence à l’ensemble des valeurs d’entrée possibles, le domaine d’un graphique est constitué de toutes les valeurs d’entrée représentées sur le graphique. Rappelez-vous que les valeurs d’entrée sont presque toujours indiquées sur l’axe horizontal du graphique. De même, puisque l’étendue est l’ensemble des valeurs de sortie possibles, l’étendue d’un graphique peut être déterminée à partir des valeurs possibles le long de l’axe vertical du graphique.
Attention : Si le graphique se poursuit au-delà du cadre, le domaine et l’étendue peuvent être plus grands que les valeurs que nous pouvons voir.
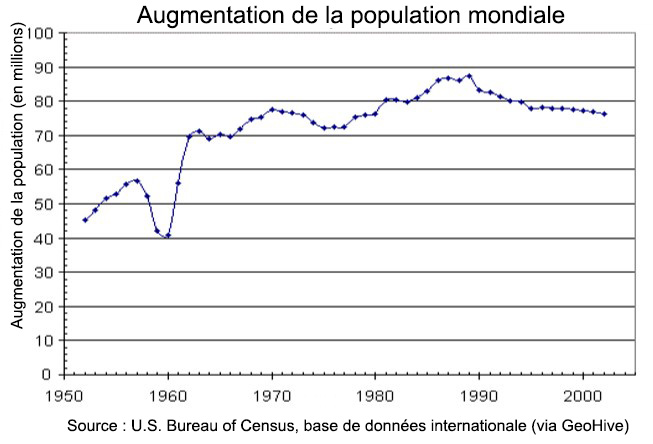
Déterminez le domaine et l’étendue du graphique ci-dessous.
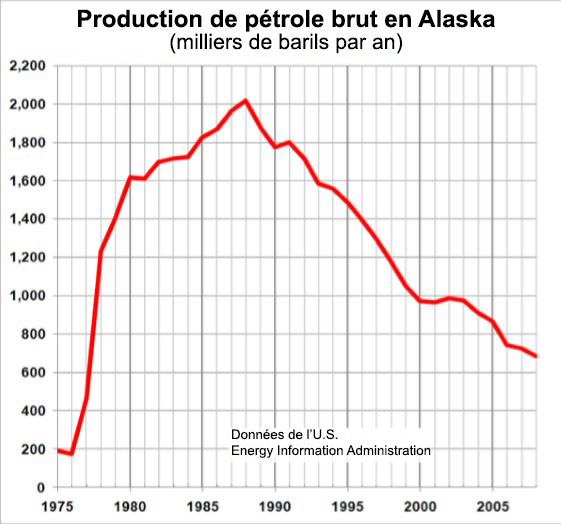
Dans le graphique ci-dessus, la quantité de l’entrée sur l’axe horizontal semble être « année », que nous pourrions noter avec la variable y. La sortie est « milliers de barils de pétrole par jour », que nous pourrions noter avec la variable b. Le graphique se poursuivrait probablement à gauche et à droite au-delà de ce qui est montré, mais selon la partie du graphique que nous voyons, nous pouvons déterminer que le domaine est 1975 ≤ y ≤ 2008, et que l’étendue est environ 180 ≤ b ≤ 2010.
Avec une notation en intervalle, le domaine serait [1975, 2008] et l’étendue serait environ [180, 2010]. Pour l’étendue, nous devons estimer les valeurs de sortie les plus petites et les plus grandes, car elles ne se situent pas exactement sur les lignes de la grille.
N’oubliez pas que, comme dans l’exemple précédent, x et y ne sont pas toujours les variables d’entrée et de sortie. L’utilisation de variables descriptives est un outil important pour se souvenir du contexte du problème.
La plupart des formules de base peuvent être évaluées à partir d’une valeur d’entrée. Les deux restrictions les plus courantes sont les suivantes :
Trouvez le domaine de chaque fonction :
a) ![]()
b) ![]()
Solution
a) Comme on ne peut pas calculer la racine carrée d’un nombre négatif, il ne faut pas que l’intérieur de la racine carrée soit négatif.
Donc, x + 4 ≥ 0 lorsque x ≥ -4.
Le domaine de f(x) est [-4, ∞).
b) On ne peut pas diviser une donnée par zéro; il faut donc que le dénominateur soit différent de zéro.
Puisque 6 – 3x = 0 lorsque x = 2, nous devons exclure 2 du domaine.
Le domaine de g(x) est (-∞, 2) ∪ (2, ∞).
Certaines fonctions ne peuvent être décrites par une seule formule.
Fonction définie par parties : une fonction définie par parties est une fonction dans laquelle la formule utilisée dépend du domaine dans lequel se trouve la valeur d’entrée. Nous notons ce concept comme suit :

Un musée demande 5 $ par personne pour une visite guidée avec un groupe de 1 à 9 personnes, ou propose un forfait de 50 $ pour un groupe de 10 personnes ou plus. Établissez une fonction reliant le nombre de personnes, n, au coût, C.
Pour établir cette fonction, deux formules différentes sont nécessaires. C = 5n fonctionnerait pour des valeurs de n inférieures à 10, et C = 50 fonctionnerait pour des valeurs de n égales ou supérieures à 10. Nous noterions donc ceci :
<img src= »https://ecampusontario.pressbooks.pub/app/uploads/sites/3867/2023/12/quicklatex.com-d280a20818f22fb33062b9e6f9a8ee46_l3-1.png » class= »ql-img-inline-formula quicklatex-auto-format » alt= »C(n)=\begin{cases} 5n\quad si \quad 0<n
Une société de téléphonie mobile utilise la fonction ci-dessous pour déterminer le coût en dollars, C, pour le transfert de g gigaoctets de données.
<img src= »https://ecampusontario.pressbooks.pub/app/uploads/sites/3867/2023/12/quicklatex.com-821ecac39d6102dd2218d064c8c4aa36_l3-1.png » class= »ql-img-inline-formula quicklatex-auto-format » alt= »C{g}=\begin{cases} 25\quad si \quad 0< g
Trouvez le coût d’utilisation de 1,5 gigaoctet de données et le coût d’utilisation de 4 gigaoctets de données.
Pour déterminer le coût d’utilisation de 1,5 gigaoctet de données, C(1,5), nous devons d’abord déterminer dans quelle partie du domaine se situe notre entrée. Comme 1,5 est inférieur à 2, nous utilisons la première formule, ce qui donne C(1,5) = 25 $.
Pour trouver le coût d’utilisation de 4 gigaoctets de données, C(4), nous constatons que notre entrée de 4 est supérieure à 2, donc nous utiliserons la deuxième formule : C(4) = 25 + 10(4 – 2) = 45 $.
Tracez le graphique de la fonction <img src= »https://ecampusontario.pressbooks.pub/app/uploads/sites/3867/2023/12/quicklatex.com-e1312123eff43d5b268f885ce3e069f0_l3-1.png » class= »ql-img-inline-formula quicklatex-auto-format » alt= »f(x)=\begin{cases} 0\quad si \quad x\le1\\ x-1\quad si \quad 14\\ \end{cases} » title= »Créé par QuickLaTeX.com » height= »79″ width= »256″ style= »vertical-align: -35px; »>
Nous pouvons tracer le graphique de chaque fonction, puis limiter le graphique au domaine indiqué. Aux extrémités du domaine, nous dessinons des cercles ouverts pour indiquer que l’extrémité n’est pas incluse en raison d’une inégalité « strictement inférieure à », et un cercle fermé pour indiquer que l’extrémité est incluse en raison d’une inégalité « inférieure ou égale à ». La première et la dernière partie sont des fonctions constantes, où la valeur de sortie est la même pour toutes les valeurs d’entrée. La partie centrale peut être considérée comme une droite et peut être représentée graphiquement si on évalue la fonction pour quelques entrées et qu’on relie les points par une ligne.
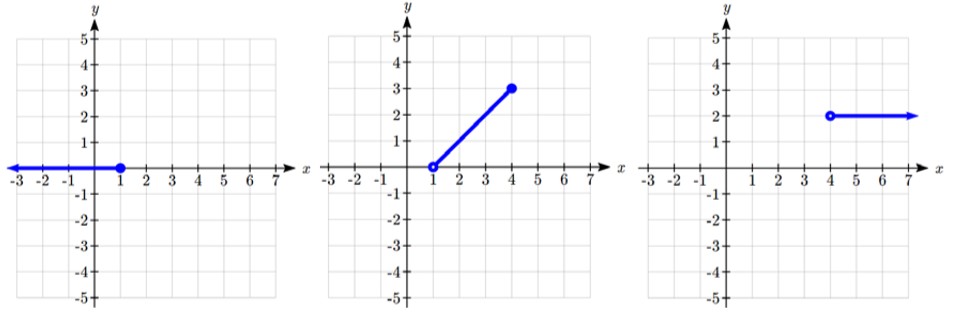
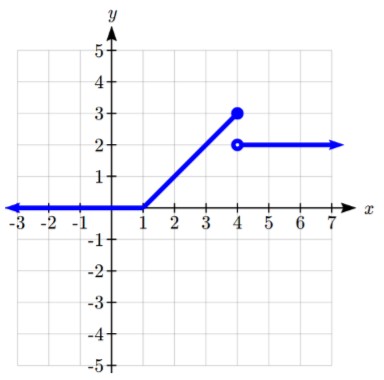
Maintenant que nous disposons de chaque pièce individuellement, nous les combinons sur le même graphique. Lorsque la première et la deuxième partie se rejoignent à x = 1, nous pouvons imaginer que le point fermé remplit le point ouvert. Comme il n’y a pas de rupture dans le graphique, il n’est pas nécessaire de montrer le point.
1. En 1960, une petite ville comptait 100 personnes. Depuis, la population a augmenté pour atteindre 1 400 personnes lors du recensement de 2010. Choisissez des variables descriptives pour vos valeurs d’entrée et de sortie et utilisez la notation en intervalle pour écrire le domaine et l’étendue.
2. En tenant compte de l’intervalle suivant, écrivez sa signification en mots, avec une notation en compréhension et avec une notation en intervalle.
3. En tenant compte du graphique ci-dessous, écrivez le domaine et l’étendue avec une notation en intervalle.
4. Dans un collège aux États-Unis, pendant l’année scolaire 2009-2010, les frais de scolarité pour les résidents de l’État étaient de 89,50 $ par crédit pour les 10 premiers crédits, de 33 $ par crédit pour les crédits 11 à 18, et de 73 $ par crédit pour les crédits supérieurs à 18. Écrivez une fonction définie par parties pour le total des frais de scolarité, T, en 2009-2010 en fonction du nombre de crédits, c. Pensez à un domaine et à une étendue raisonnables.
5. Examinez le graphique ci-dessous et indiquez les éléments suivants avec à la fois une notation en compréhension et une notation en intervalle.
14
Puisque les fonctions représentent la manière dont une variable de sortie varie en fonction d’une variable d’entrée, il est naturel de s’interroger sur la vitesse à laquelle les valeurs de la fonction changent.
Par exemple, la fonction C(t) ci-dessous donne le coût moyen, en dollars, d’un gallon d’essence t années après 2000.
| t | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| C(t) | 1,47 | 1,69 | 1,94 | 2,30 | 2,51 | 2,64 | 3,01 | 2,14 |
Si nous nous intéressons à l’évolution du prix de l’essence entre 2002 et 2009, nous pouvons calculer que le coût du gallon est passé de 1,47 $ à 2,14 $, soit une augmentation de 0,67 $. Bien que cela soit intéressant, il serait peut-être plus utile d’examiner l’évolution du prix par année. Vous avez probablement remarqué que le prix n’a pas varié de la même manière chaque année. Nous devrions donc trouver le taux de variation moyen sur une période donnée.
Le prix du gaz a augmenté de 0,67 $ de 2002 à 2009, sur une période de 7 ans, soit une moyenne de ![]() $ par année. En moyenne, le prix du gaz a donc augmenté d’environ 9,6 sous par année.
$ par année. En moyenne, le prix du gaz a donc augmenté d’environ 9,6 sous par année.
Voici d’autres exemples de dérivées :
Taux de variation moyen : le taux de variation moyen entre deux valeurs d’entrée est la variation totale des valeurs de la fonction (valeurs de sortie) divisée par la variation des valeurs d’entrée.
Taux de variation moyen = ![]()
En utilisant la fonction du coût du gaz présentée plus haut, trouvez le taux de variation moyen entre 2007 et 2009.
D’après le tableau, le coût du gaz était de 2,64 $ en 2007. En 2009, le coût était de 2,14 $.
L’entrée (le nombre d’années) a varié de 2 unités. La sortie a varié de 2,14 $ – 2,64 $ = -0,50 $. Le taux de variation moyen est donc ![]() $ par année.
$ par année.
Remarquez que dans le dernier exemple, la variation de la sortie est négative puisque la valeur de sortie de la fonction a diminué. Par conséquent, le taux de variation moyen est négatif.
À l’aide de la fonction g(t) représentée ici, trouvez le taux de variation moyen sur l’intervalle [0, 3].
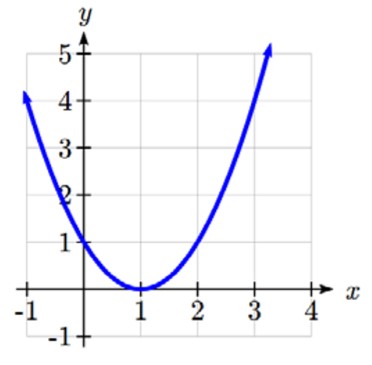
À t = 0, le graphique montre g(0) = 1.
À t = 3, le graphique montre g(3) = 4.
La sortie a varié de 3 et l’entrée a varié de 3, ce qui donne un taux de variation moyen de :
![]()
Lors d’un voyage en voiture, après avoir récupéré votre ami qui habite à 16 km, vous décidez de noter la distance qui vous sépare de votre domicile au fil du temps. Trouvez votre vitesse moyenne sur les 6 premières heures.
| t (heures) | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| D(t) (km) | 16 | 95 | 170 | 265 | 364 | 432 | 538 | 625 |
Ici, votre vitesse moyenne correspond au taux de variation moyen.
Vous avez parcouru 538 km en 6 heures, soit une vitesse moyenne de :
![]() km par heure.
km par heure.
Nous pouvons effectuer le calcul du taux de variation moyen de manière plus formelle en utilisant la notation fonctionnelle.
Taux de variation moyen à l’aide de la notation fonctionnelle : pour une fonction f(x), le taux de variation moyen sur l’intervalle [a, b] est le suivant :
Taux de variation moyen = ![]()
Calculez le taux de variation moyen de ![]() sur l’intervalle [2, 4].
sur l’intervalle [2, 4].
Nous pouvons commencer par calculer les valeurs de la fonction à chaque extrémité de l’intervalle :
![]()
![]()
Calculez maintenant le taux de variation moyen :
Taux de variation moyen = ![]()
La force magnétique F entre deux aimants, mesurée en Newtons, est liée à la distance entre les aimants d, en centimètres, par la formule ![]() . Trouvez le taux de variation moyen de la force si la distance entre les aimants passe de 2 cm à 6 cm.
. Trouvez le taux de variation moyen de la force si la distance entre les aimants passe de 2 cm à 6 cm.
Nous calculons le taux de variation moyen de ![]() sur l’intervalle [2, 6].
sur l’intervalle [2, 6].
| Taux de variation moyen = | Évaluation de la fonction |
| Simplification | |
| Combinaison des termes du numérateur | |
| Simplification supplémentaire | |
Cela nous indique que la force magnétique diminue, en moyenne, de 1/9 Newtons par centimètre au cours de cet intervalle.
Dans le cadre de l’étude de l’évolution des fonctions, il est intéressant d’étudier le comportement graphique des fonctions.
Fonction croissante/décroissante :
Une fonction est croissante dans un intervalle si ses valeurs augmentent au fur et à mesure que les valeurs d’entrée augmentent. Plus précisément, une fonction est croissante si f(b) > f(a) pour deux valeurs d’entrée quelconques a et b dans l’intervalle avec b > a. Le taux de variation moyen d’une fonction croissante est positif.
Une fonction est décroissante dans un intervalle si ses valeurs diminuent au fur et à mesure que les valeurs d’entrée augmentent. Plus précisément, une fonction est décroissante si f(b) < f(a) pour deux valeurs d’entrée quelconques a et b dans l’intervalle avec b > a. Le taux de variation moyen d’une fonction décroissante est négatif.
Compte tenu de la fonction p(t) représentée ici, sur quels intervalles la fonction semble-t-elle croissante?
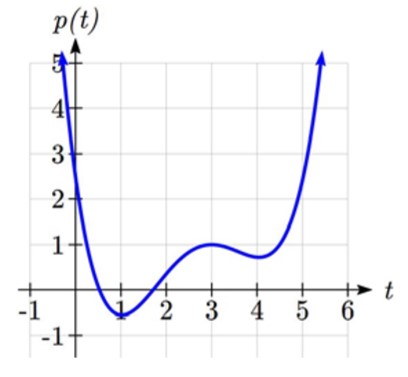
La fonction semble croissante de t = 1 à t = 3, et à partir de t = 4.
Avec une notation en intervalle, nous dirions que la fonction semble croissante sur l’intervalle (1, 3) et sur l’intervalle (4, ∞).
Remarquez que dans le dernier exemple, nous avons utilisé des intervalles ouverts (intervalles qui n’incluent pas les extrémités) puisque la fonction n’est ni croissante ni décroissante à t = 1, 3, ou 4.
Extremums locaux : le point où une fonction passe d’une fonction croissante à une fonction décroissante est appelé un maximum local.
Le point où une fonction passe d’une fonction décroissante à une fonction croissante est appelé un minimum local.
Ensemble, les maximums et les minimums locaux sont appelés les extremums locaux, ou valeurs extrêmes locales, de la fonction.
En utilisant la fonction du coût de l’essence présentée au début du chapitre, trouvez un intervalle sur lequel la fonction semble décroissante. Estimez les extremums locaux à l’aide du tableau.
| t | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| C(t) | 1,47 | 1,69 | 1,94 | 2,30 | 2,51 | 2,64 | 3,01 | 2,14 |
Il semble que le coût de l’essence ait augmenté de t = 2 à t = 8, et qu’il ait diminué de t = 8 à t = 9, de sorte que la fonction semble être décroissante sur l’intervalle (8, 9).
Puisque la fonction semble passer de croissante à décroissante à t = 8, il y a un maximum local à t = 8.
1. En utilisant la fonction du coût du gaz présentée plus haut, trouvez le taux de variation moyen entre 2003 et 2008.
2. Calculez le taux de variation moyen de ![]() sur l’intervalle [1, 9].
sur l’intervalle [1, 9].
3. Calculez le taux de variation moyen de ![]() sur l’intervalle [a, a + h].
sur l’intervalle [a, a + h].
4. Utilisez le graphique suivant de la fonction ![]() pour estimer les extremums locaux de la fonction. Déterminez les intervalles sur lesquels la fonction est croissante et décroissante.
pour estimer les extremums locaux de la fonction. Déterminez les intervalles sur lesquels la fonction est croissante et décroissante.
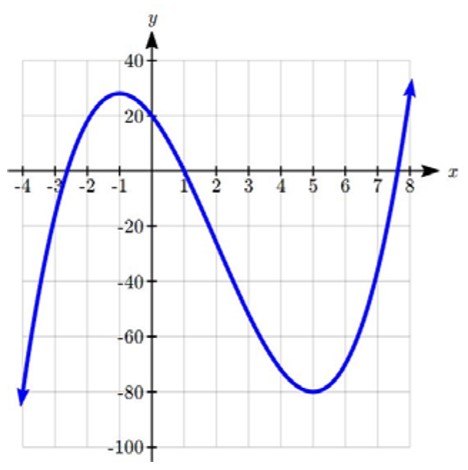
5. Examinez le graphique ci-dessous et répondez aux questions suivantes.
15
Fonctions quadratiques
Dans cette section, nous allons explorer les fonctions quadratiques, un type de fonction polynomiale. Les fonctions quadratiques modélisent souvent des problèmes impliquant des surfaces, ou des revenus et des bénéfices, ce qui donne lieu à des applications intéressantes.
Une agricultrice souhaite délimiter un espace rectangulaire pour y aménager un nouveau jardin. Elle a acheté 80 pieds de grillage pour clôturer trois côtés, et placera le quatrième côté contre la clôture de la cour. Trouvez une formule pour calculer la surface entourée par la clôture si les côtés de la clôture qui sont perpendiculaires à la clôture existante ont une longueur L.
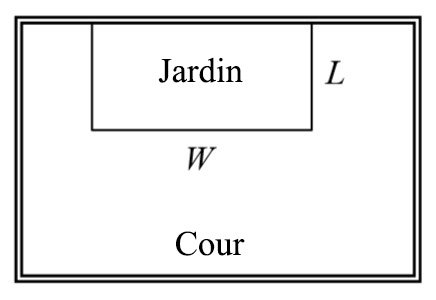
Dans un scénario de géométrie comme celui-ci, il est souvent utile de faire un dessin. Il peut également être utile d’introduire une variable temporaire, W, pour représenter le côté de la clôture parallèle au quatrième côté ou à la clôture de la cour.
Comme nous savons que nous ne disposons que de 80 pieds de grillage, nous savons que L + W + L = 80, ou plus simplement, 2L + W = 80. Cela nous permet de représenter la largeur, W, en fonction de L : W = 80 – 2L
Nous pouvons maintenant écrire une équation pour la surface entourée par la clôture. Nous savons que la surface d’un rectangle correspond à la longueur multipliée par la largeur :
A = LW = L (80 – 2L)
A (L) = 80L – 2L2
Cette formule représente la surface de la clôture en fonction de la longueur variable L.
Nous allons maintenant explorer les caractéristiques des graphiques des fonctions quadratiques. Outre les points d’intersection, les fonctions quadratiques ont un sommet à l’endroit où elles changent de direction.
La forme standard des fonctions quadratiques est ![]() , mais vous les verrez souvent écrites sous la forme
, mais vous les verrez souvent écrites sous la forme ![]() . Pour comprendre pourquoi, prenons l’exemple suivant.
. Pour comprendre pourquoi, prenons l’exemple suivant.
Dessinez un graphique pour ![]() :
:
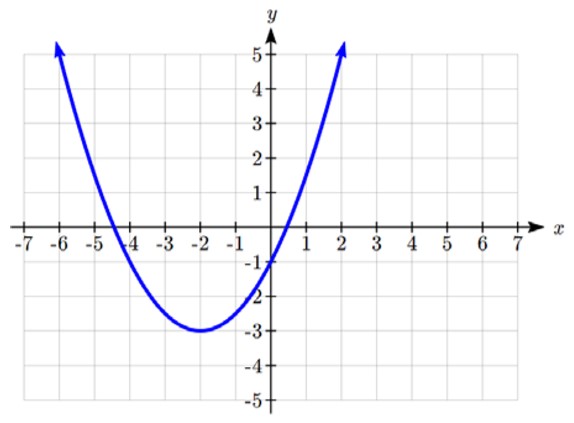
Nous pouvons créer un tableau de valeurs, que nous pouvons utiliser pour tracer plusieurs points et relier ceux-ci par une courbe régulière.
| x | g(x) |
| -5 | 1,5 |
| -4 | -1 |
| -3 | -2,5 |
| -2 | -3 |
| -1 | -2,5 |
| 0 | -1 |
| 1 | 1,5 |
Remarquez que le point d’inflexion du graphique, où la fonction passe de décroissante à croissante, se situe au point (-2, -3). Nous appelons ce point le sommet de la fonction quadratique. Remarquez que ![]() peut aussi s’écrire
peut aussi s’écrire ![]() . En comparant cela à la forme
. En comparant cela à la forme ![]() , vous pouvez voir que le sommet du graphique, (-2, -3), correspond au point (h, k).
, vous pouvez voir que le sommet du graphique, (-2, -3), correspond au point (h, k).
Formes des fonctions quadratiques :
La forme standard d’une fonction quadratique est ![]() .
.
La forme de sommet d’une fonction quadratique est ![]() .
.
Le sommet de la fonction quadratique est situé en (h, k), où h et k sont les nombres de la forme du sommet de la fonction.
Lorsque a > 0, le graphique de la fonction quadratique s’ouvre vers le haut.
Lorsque a < 0, le graphique de la fonction quadratique s’ouvre vers le bas.
| Dessinez un graphique pour Pour l’écrire sous forme polynomiale standard, nous pouvons développer la formule et simplifier les termes :
Dans l’exemple précédent, nous avons vu qu’il est possible de réécrire une fonction quadratique donnée sous la forme d’un sommet, sous forme standard en développant la formule. Il serait utile d’inverser ce processus, puisque la forme transformée nous donnerait le sommet. Trouver le sommet d’une fonction quadratique : pour une fonction quadratique donnée sous forme standard, le sommet (h, k) est situé à :
Trouvez le sommet de la fonction quadratique La coordonnée horizontale du sommet (abscisse) sera à La coordonnée verticale du sommet (ordonnée) sera à Lorsque vous réécrivez la fonction sous forme de sommet, la valeur de a reste la même que dans la fonction quadratique d’origine. En plus de nous permettre de tracer plus facilement le graphique d’une fonction quadratique écrite sous forme standard, la recherche du sommet a une autre fonction importante : elle nous permet de déterminer la valeur maximale ou minimale de la fonction, selon la direction dans laquelle le graphique s’ouvre.
Pour en revenir à notre agricultrice du début du chapitre, quelles dimensions devrait-elle donner à son jardin pour maximiser la surface clôturée? Plus tôt, nous avons déterminé que la surface qu’elle pouvait entourer avec 80 pieds de clôture sur trois côtés était donnée par l’équation A(L) = 80L – 2L2. Remarquez que la fonction quadratique a été réfléchie verticalement, puisque le coefficient du terme au carré est négatif, de sorte que le graphique s’ouvrira vers le bas et que le sommet sera une valeur maximale pour la surface. Pour trouver le sommet, nous savons que a est le coefficient du terme au carré, donc a = -2, b = 80, et c = 0. Pour trouver le sommet : La valeur maximale de la fonction est une surface de 800 pieds carrés, qui se produit lorsque L = 20 pieds. Si les côtés les plus courts mesurent 20 pieds, il reste donc 40 pieds de clôture pour le côté le plus long. Pour maximiser la superficie, l’agricultrice doit donc entourer son jardin de manière à ce que les deux côtés les plus courts aient une longueur de 20 pieds, et que le côté le plus long, parallèle à la clôture existante, ait une longueur de 40 pieds.
Comportement à l’origine : Points d’intersectionComme pour toute fonction, nous pouvons trouver les points d’intersection sur l’ordonnée à l’origine d’une fonction quadratique en évaluant la fonction à une valeur d’entrée de zéro, et nous pouvons trouver les points d’intersection sur l’abscisse à l’origine en résolvant le moment où la valeur de sortie sera de zéro. Remarquez que, selon la position du graphique, nous pouvons avoir une ou deux points d’intersection sur l’abscisse à l’origine, ou aucune.
Nous pouvons déterminer les points d’intersection sur l’ordonnée à l’origine et sur l’abscisse à l’origine d’une fonction quadratique à l’aide de la formule quadratique. Formule quadratique : pour une fonction quadratique donnée sous forme standard
Une balle est lancée du haut d’un immeuble de 40 pieds à une vitesse de 80 pieds par seconde. La hauteur de la balle au-dessus du sol peut être modélisée par l’équation suivante :
Quelle est la hauteur maximale de la balle? À quel moment la balle touche-t-elle le sol? Pour trouver la hauteur maximale de la balle, nous devons connaître le sommet de la fonction quadratique.
La balle atteint une hauteur maximale de 140 pieds après 2,5 secondes. Pour savoir à quel moment la balle touche le sol, nous devons déterminer le moment où la hauteur est nulle, c’est-à-dire lorsque H(t) = 0. Nous pourrions le faire en utilisant la forme transformée de la fonction, mais nous pouvons aussi utiliser la formule quadratique :
Puisque la racine carrée ne se simplifie pas facilement, nous pouvons utiliser une calculatrice pour obtenir les valeurs approximatives des solutions :
La deuxième réponse se situe en dehors du domaine raisonnable de notre modèle, et nous concluons donc que la balle touchera le sol après environ 5,458 secondes.
L’offre d’un certain produit peut être modélisée par Rappelons que le prix et la quantité d’équilibre sont déterminés par l’intersection de la courbe de l’offre et de la courbe de la demande. Nous pouvons trouver ce point d’intersection en mettant les équations à égalité :
Comme cela n’a pas de sens de parler de quantités négatives, la quantité d’équilibre est q = 18. Pour trouver le prix d’équilibre, nous évaluons une fonction ou l’autre à la quantité d’équilibre.
La quantité d’équilibre est donc de 18 000 articles, au prix de 972 $.
Exercices pratiques1. Une grille de coordonnées a été superposée à la trajectoire quadratique d’un ballon de basketball. Trouvez une équation pour la trajectoire du ballon. Celui-ci réussit-il à entrer dans le panier?  2. Écrivez 3. Pour ces deux équations, déterminez si le sommet sera une valeur maximale ou une valeur minimale. 4. Réécrivez l’équation suivante sous forme de sommet : 5. Une nouvelle entreprise a déterminé que ses profits quotidiens, P, provenant de la vente de x boîtes de masques respiratoires N95 sont donnés par la formule suivante : 6. Une balle est lancée du haut d’un immeuble de 35 mètres à une vitesse de 24,5 mètres par seconde. La hauteur de la balle au-dessus du sol peut être modélisée par l’équation suivante :
|
16
1. Domaine : y = années [1960, 2010]; étendue : p = population [100, 1 400]
2. a. Valeurs inférieures ou égales à -2, ou valeurs supérieures ou égales à -1, et inférieures à 3
b. {x | x ≤ -2 or -1 ≤ x < 3}
c. (-∞, -2] ∪ [-1, 3)
3. Domaine : y = années [1952, 2002]; étendue : p = population en millions de personnes [40, 88]
4. <img src= »https://ecampusontario.pressbooks.pub/app/uploads/sites/3867/2023/12/quicklatex.com-87e97341b2996e0889c8a34873751f95_l3-1.png » class= »ql-img-inline-formula quicklatex-auto-format » alt= »T(c)=\begin{cases} 89,5c \quad si \quad c\le10\\ 895+33(c-10)\quad si \quad 1018\\ \end{cases} » title= »Créé par QuickLaTeX.com » height= »79″ width= »715″ style= »vertical-align: -35px; »>
Les nombres entiers de 0 à (les réponses peuvent varier), par exemple [0,23], constituent un domaine raisonnable. Une étendue raisonnable serait de 0 $ à (les réponses peuvent varier), par exemple [0,1524].
5. a. {x | 2008 ≤ x ≤ 2018}, [2008, 2018]
b. {x | 16,1 ≤ x ≤ 88.4}, [16.1, 88,4]
1.![]() 0,264 $ par année
0,264 $ par année
2. Taux de variation moyen = ![]()
3. ![]()
4. D’après le graphique, le maximum local semble être à (-1, 28), et le minimum local, à (5, -80). La fonction est croissante sur (-∞, -1)∪(5, ∞) et décroissante sur (-1, 5).
5. a. -0,59 par 100 000
b. 6
c. 2010, 2014, et 2017
1. La trajectoire passe par l’origine et a pour sommet (-4, 7).
2.![]() sous forme standard;
sous forme standard; ![]() sous forme de sommet.
sous forme de sommet.
3. a. Le sommet est une valeur minimum (s’ouvre vers le haut).
b. Le sommet est une valeur maximum (s’ouvre vers le bas).
4. ![]()
5. 5 387,50 $
6. a. ![]() mètres
mètres
b. ![]() secondes
secondes
IV
17
Fonctions exponentielles
L’Inde est le deuxième pays le plus peuplé du monde, avec une population d’environ 1,14 milliard de personnes en 2008. La population augmente d’environ 1,34 % par année. Nous pourrions nous demander si nous pouvons trouver une formule pour modéliser la population, P, en fonction du temps, t, dans les années après 2008, si la population continue à augmenter à ce rythme.
Dans le cas d’une croissance linéaire, le taux de changement est constant, c’est-à-dire que le résultat augmente pour chaque augmentation de l’entrée. Par exemple, dans l’équation ![]() , la pente nous indique que le résultat augmente de 3 chaque fois que l’entrée augmente de 1. Ce scénario démographique est différent – nous avons un taux de variation en pourcentage plutôt qu’un nombre constant de personnes comme taux de variation. Pour comprendre l’importance de cette différence, prenons l’exemple de ces deux entreprises :
, la pente nous indique que le résultat augmente de 3 chaque fois que l’entrée augmente de 1. Ce scénario démographique est différent – nous avons un taux de variation en pourcentage plutôt qu’un nombre constant de personnes comme taux de variation. Pour comprendre l’importance de cette différence, prenons l’exemple de ces deux entreprises :
L’entreprise A possède 100 magasins et elle prend de l’expansion en ouvrant 50 nouveaux magasins par année.
L’entreprise B possède 100 magasins et prend de l’expansion en augmentant le nombre de ses magasins de 50 % chaque année.
Ces entreprises devraient connaître quelques années de croissance :
| Année | Magasins, entreprise A | Magasins, entreprise B |
| 0 | 100 | En commençant avec 100 chacune | 100 |
| 1 | 100 + 50 = 150 | Elles ont toutes 50 magasins de plus au cours de la première année. | 100 + 50 % de 100 100 + 0,50(100) = 150 |
| 2 | 150 + 50 = 200 | Le nombre de magasins de l’entreprise A augmente de 50 et le nombre de magasins de l’entreprise B de 75. | 150 + 50 % de 150 150 + 0,50(150) = 225 |
| 3 | 200 + 50 = 250 | Le nombre de magasins de l’entreprise A augmente de 50 et le nombre de magasins de l’entreprise B de 112,5. | 225 + 50 % de 225 225 + 0,50(225) = 337,5 |
Remarquez qu’avec le taux de croissance en pourcentage, la croissance de l’entreprise est de 50 % du total de l’année en cours, de sorte qu’à mesure que l’entreprise croit, le nombre de magasins ajoutés en un an augmente également.
Pour essayer de simplifier les calculs, on remarque qu’au bout d’un an, le nombre de magasins de l’entreprise B était le suivant :
100 + 0,50(100) ou l’équivalent par factorisation
100(1 + 0,50) = 150
On peut dire que « le nouveau nombre de magasins correspond aux 100 % initiaux, plus 50 % ».
Après 2 ans, le nombre de magasins était de :
150 + 0,50(150) ou l’équivalent par factorisation
150(1 + 0,50) Rappelons maintenant que le nombre de 150 provient de l’équation 100(1 + 0,50). Remplaçons-le :
100(1 + 0,50)(1 + 0,50) = 100(1 + 0,50)2 = 225.
Après 3 ans, le nombre de magasins était de :
225 + 0,50(225) ou l’équivalent par factorisation
225(1 + 0,50) Maintenant, il faut se rappeler que le nombre 225 vient de l’équation 100(1 + 0,50)2. Remplaçons-le :
100(1 + 0,50)2(1 + 0,50) = 100(1 + 0,50)3 = 337,5.
À partir de là, nous pouvons généraliser, en remarquant que pour montrer une augmentation de 50 %, nous multiplions chaque année par un facteur de (1 + 0,50), de sorte qu’après n années, notre équation serait la suivante :
B(n) = 100(1 + 0,50)n
Dans cette équation, 100 représente la quantité initiale et 0,50 le taux de croissance en pourcentage. En généralisant davantage, nous obtenons la forme générale des fonctions exponentielles.
Fonction exponentielle : une fonction de croissance ou de décroissance exponentielle est une fonction qui augmente ou diminue à un taux de croissance constant. L’équation peut être écrite sous la forme suivante :
![]() ou
ou ![]() , où
, où ![]()
Où :
a est la valeur initiale ou de départ de la fonction
r est le taux de croissance ou de décroissance en pourcentage, exprimé en décimales
b est le facteur de croissance ou multiplicateur de croissance Les puissances de nombres négatifs ayant un comportement étrange, nous limitons b aux valeurs positives.
Pour mieux comprendre la différence entre une croissance exponentielle et une croissance linéaire, comparez les deux tableaux et graphiques ci-dessous, qui illustrent la croissance des entreprises A et B décrites ci-dessus sur une période plus longue si les schémas de croissance devaient se poursuivre.
| Année | Entreprise A | Entreprise B |
| 2 | 200 | 225 | 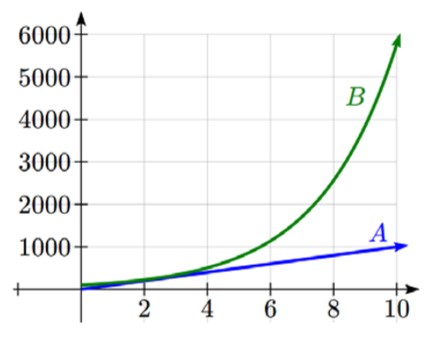 | |
| 4 | 300 | 506 | ||
| 6 | 400 | 1 139 | ||
| 8 | 500 | 2 563 | ||
| 10 | 600 | 5 767 |
Écrivez une fonction exponentielle pour la population de l’Inde et utilisez-la pour prédire la population en 2020.
Au début du chapitre, nous avons appris que la population de l’Inde s’élevait à 1,14 milliard de personnes en 2008 et que le taux de croissance était de 1,34 %. Avec 2008 comme date de départ (t = 0), notre population initiale sera de 1,14 milliard de personnes. Le taux de croissance étant de 1,34 %, notre valeur de r est de 0,0134.
En utilisant la formule de base pour la croissance exponentielle ![]() , nous pouvons écrire la formule,
, nous pouvons écrire la formule, ![]() .
.
Pour estimer la population en 2020, nous évaluons la fonction à t = 12, puisque 2020 est 12 ans après 2008.
Ainsi, ![]() milliard de personnes en 2020.
milliard de personnes en 2020.
Un certificat de placement garanti (CPG) est un type de compte d’épargne proposé par les banques, qui offre généralement un taux d’intérêt plus élevé en échange d’une durée fixe pendant laquelle vous laissez votre argent investi. Si une banque offre un CPG de 24 mois avec un taux d’intérêt annuel de 1,2 % composé mensuellement, à combien s’élèvera un investissement de 1 000 $ au cours de ces 24 mois?
Tout d’abord, il faut noter que le taux d’intérêt est un taux annuel, mais qu’il est composé mensuellement, ce qui signifie que les intérêts sont calculés et ajoutés au compte tous les mois.
Pour obtenir le taux d’intérêt mensuel, nous divisons le taux annuel de 1,2 % par 12 puisqu’il y a 12 mois dans une année : 1,2 % / 12 = 0,1 %. Chaque mois, nous percevrons un intérêt de 0,1 %.
À partir de là, nous pouvons établir une fonction exponentielle, avec notre montant initial de 1 000 $ et un taux de croissance de r = 0,001, et notre entrée m mesurée en mois.
![]()
![]()
Après 24 mois, le solde du compte aura augmenté pour atteindre : ![]() .
.
Dans tous les exemples précédents, nous avons assisté à une croissance exponentielle. Les fonctions exponentielles peuvent également être utilisées pour modéliser des quantités qui diminuent à un taux constant. La désintégration radioactive en est un exemple : les isotopes radioactifs de certains atomes se transforment en atomes d’un type différent, ce qui entraîne une diminution du pourcentage de la matière d’origine au fil du temps.
Le bismuth 210 est un isotope qui se désintègre par radioactivité d’environ 13 % chaque jour, ce qui signifie que 13 % du bismuth 210 restant se transforme en un autre atome (polonium 210 dans ce cas) chaque jour. Si vous commencez avec 100 mg de bismuth 210, quelle quantité restera-t-il après une semaine?
Dans le cas de la désintégration radioactive, au lieu que la quantité augmente à un taux de pourcentage, elle diminue. Notre quantité initiale est a = 100 mg, et notre taux de croissance sera négatif de 13 %, puisque nous sommes en décroissance : r = -0,13. On obtient ainsi l’équation :
![]()
Cela peut également s’expliquer ainsi : si 13 % se désintègrent, il reste 87 %.
Après une semaine, sept jours, la quantité restante serait de ![]() mg de bismuth 210.
mg de bismuth 210.
T(q) représente le nombre total de contrats de téléphones intelligents Android, en milliers, détenus par une certaine région de magasins Rogers, mesuré trimestriellement depuis le 1er janvier 2010. Interprétez toutes les parties de l’équation : ![]() .
.
En interprétant cela à partir de la forme exponentielle de base, nous savons que 86 est notre valeur initiale. Cela signifie qu’au 1er janvier 2010, cette région comptait 86 000 contrats de téléphones intelligents Android. Puisque b = 1 + r = 1,64, nous savons que chaque trimestre, le nombre de contrats de téléphones intelligents augmente de 64 %. T(2) = 231,3056 signifie qu’au cours du 2etrimestre (ou à la fin du 2e trimestre), il y avait environ 231 305 contrats de téléphones intelligents Android.
Dans les exemples précédents, nous avons pu écrire des équations pour les fonctions exponentielles puisque nous connaissions la quantité initiale et le taux de croissance. Si nous ne connaissons pas le taux de croissance, mais seulement quelques paires de valeurs d’entrée et de sortie, nous pouvons toujours construire une fonction exponentielle.
En 2002, une entreprise possédait 80 magasins de détail. En 2008, elle en comptait 180. Si l’entreprise connaît une croissance exponentielle, trouvez une formule pour la fonction.
Si nous définissons notre variable d’entrée comme étant t années après 2002, les renseignements énumérés peuvent être écrits sous la forme de deux paires d’entrées-sorties : (0, 80) et (6, 180). Remarquez qu’en choisissant de mesurer notre variable d’entrée en nombre d’années après la valeur de la première année fournie, nous nous sommes effectivement « donné » la valeur initiale de la fonction : a = 80. Ce qui nous donne une équation sous la forme f(t) = 80bt.
La substitution de notre deuxième paire d’entrées-sorties nous permet de résoudre b :
![]() Divisez par 80.
Divisez par 80.
![]() Prenez la racine 6 des deux côtés.
Prenez la racine 6 des deux côtés.
![]()
Nous obtenons ainsi l’équation de la population :
![]()
Rappelons que, puisque b = 1 + r, nous pouvons interpréter ce résultat comme signifiant que le taux de croissance de la population est r = 0,1447, et que la population augmente donc d’environ 14,47 % chaque année.
Dans cet exemple, vous auriez également pu utiliser ![]() pour évaluer la racine 6 si votre calculatrice n’a pas de bouton pour la racine n. Nous avons choisi d’utiliser la forme f(x) = abx de la fonction exponentielle plutôt que la forme f(x) = a (1 + r)x, mais ce choix était totalement arbitraire – l’une ou l’autre forme aurait pu être utilisée.
pour évaluer la racine 6 si votre calculatrice n’a pas de bouton pour la racine n. Nous avons choisi d’utiliser la forme f(x) = abx de la fonction exponentielle plutôt que la forme f(x) = a (1 + r)x, mais ce choix était totalement arbitraire – l’une ou l’autre forme aurait pu être utilisée.
Lors de la recherche d’équations, la valeur de b ou de r doit généralement être arrondie pour pouvoir être écrite facilement. Pour préserver la précision, il est important de ne pas arrondir ces valeurs. En règle générale, il faut veiller à conserver au moins trois chiffres significatifs dans le taux de croissance. Par exemple, si votre valeur de r est de 0,00317643, vous voudrez l’arrondir au maximum à 0,00318.
Pour avoir une idée du comportement des valeurs exponentielles, commençons par examiner de plus près la fonction f(x) = 2x. Liste d’une table de valeurs pour cette fonction :
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| f(x) | 1 | 2 | 4 | 8 |
Remarquez que :
Examen de la fonction ![]()
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| g(x) | 8 | 4 | 2 | 1 |
Notez que cette fonction est également positive pour toutes les valeurs de x, mais dans ce cas, elle augmente lorsque x diminue, et diminue vers zéro lorsque x augmente. C’est un exemple de décroissance exponentielle. Vous pouvez remarquer dans le tableau que cette fonction semble être la réflexion horizontale du tableau f(x) = 2x. C’est effectivement le cas :
L’examen des graphiques confirme également cette relation :
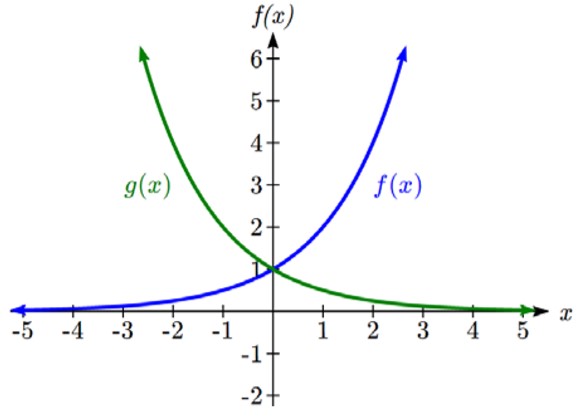
Examinez une fonction pour la formule f(x) = abx. Puisque a, que nous avons appelé la valeur initiale dans la dernière section, est la valeur de la fonction à une entrée de zéro, a nous donnera le point d’intersection sur l’ordonnée à l’origine du graphique. Les graphiques ci-dessus montrent qu’un graphique exponentiel présente une asymptote horizontale d’un côté et qu’il peut augmenter ou diminuer en fonction du facteur de croissance. Une asymptote horizontale est une ligne horizontale y = b où le graphique se rapproche de la ligne lorsque les entrées sont importantes. L’asymptote horizontale nous aidera à déterminer le comportement à long terme et elle est facile à déterminer à partir du graphique.
Le graphique s’agrandit lorsque le taux de croissance est positif, ce qui fait que le facteur de croissance b est supérieur à 1. S’il est négatif, le facteur de croissance sera inférieur à 1.
Caractéristiques graphiques des fonctions exponentielles :
Lorsque l’on dessine le graphique d’une fonction exponentielle, il peut être utile de se rappeler que le graphique passe par les points (0, a) et (1, ab).
La valeur b déterminera le comportement à long terme de la fonction :
Si b > 1, alors que x→∞, f(x)→∞ et que x→-∞, f(x)→0.
Si 0 < b < 1, alors que x→∞ , f(x)→0 et que x→-∞, f(x)→∞.
Dessinez un graphique de ![]() .
.
Ce graphique aura un point d’intersection sur l’ordonnée à l’origine à (0, 4), et passera par le point (1, ![]() ). Puisque b < 1, le graphique sera décroissant vers zéro. Puisque a > 0, le graphique sera concave vers le haut.
). Puisque b < 1, le graphique sera décroissant vers zéro. Puisque a > 0, le graphique sera concave vers le haut.
Nous pouvons aussi voir la tendance à long terme sur le graphique : alors que x→∞, f(x)→0 et que x→-∞, f(x)→∞.
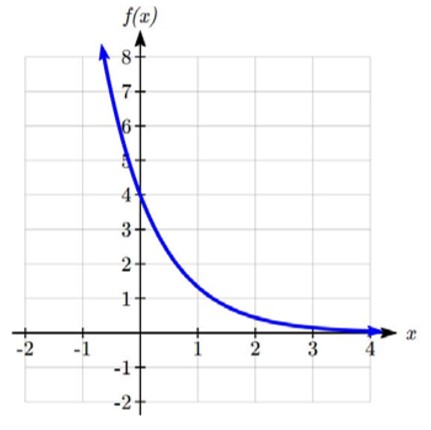
Pour mieux comprendre l’effet de a et b sur le graphique, examinez les ensembles de graphiques ci-dessous. Le premier ensemble montre différents graphiques, où a reste le même et où nous ne changeons que la valeur de b.
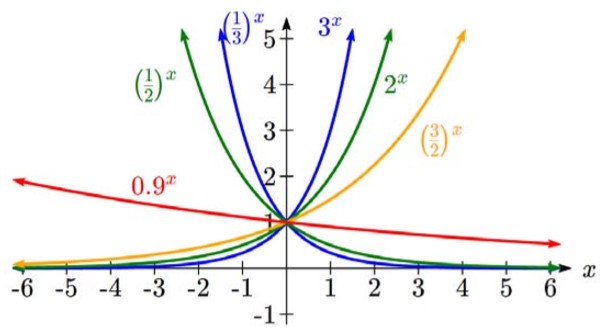
Remarquez que plus la valeur de b est proche de 1, moins le graphique est abrupt.
Dans l’ensemble suivant de graphiques, a est modifié et notre valeur pour b reste la même.
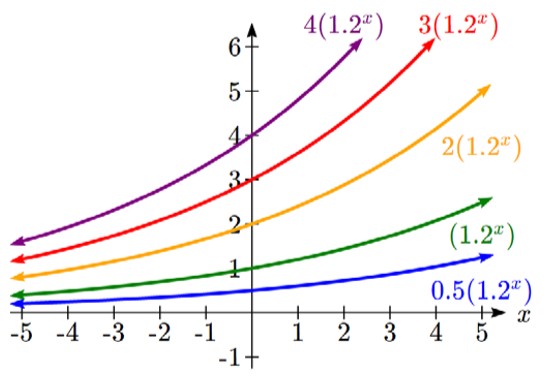
Remarquez que le changement de la valeur de a modifie le point d’intersection sur l’ordonnée à l’origine. Puisque a multiplie le terme bx, a agit comme un facteur d’étirement vertical, et non comme un décalage. Remarquez également que le comportement à long terme de toutes ces fonctions est le même parce que le facteur de croissance n’a pas changé et qu’aucune de ces valeurs a n’a introduit un renversement vertical.
Faites correspondre chaque équation avec son graphique.
| 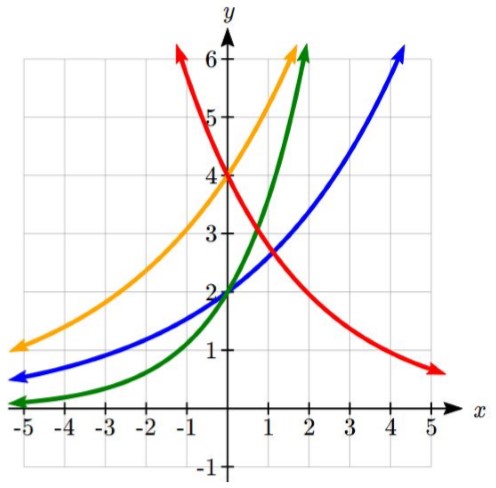 |
Le graphique de k(x) est le plus facile à identifier, car il s’agit de la seule équation dont le facteur de croissance est inférieur à 1, ce qui produit un graphique décroissant. Le graphique de h(x) peut être identifié comme la seule fonction exponentielle croissante dont le point d’intersection sur l’ordonnée à l’origine est situé à (0, 4). Les graphiques de f(x) et g(x) ont tous deux un point d’intersection sur l’ordonnée à l’origine à (0, 2), mais comme g(x) a un facteur de croissance plus important, nous pouvons l’identifier comme étant le graphique qui augmente le plus rapidement.
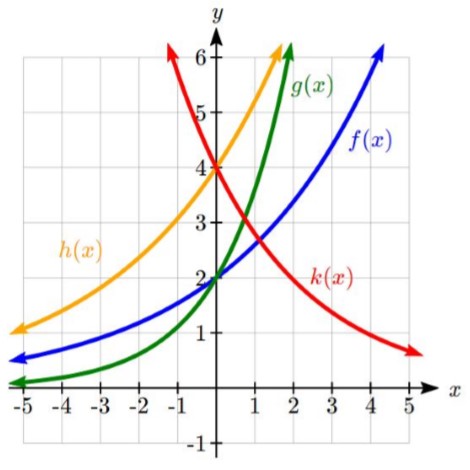
Dans l’exemple du certificat de placement garanti (CPG) présenté plus haut dans la section, nous avons rencontré les intérêts composés. En règle générale, les comptes bancaires et les autres instruments d’épargne dans lesquels les revenus sont réinvestis, comme les fonds communs de placement et les comptes de retraite, utilisent les intérêts composés. Le terme « capitalisation » (intérêts composés) vient du fait que les intérêts sont perçus non pas sur la valeur initiale, mais sur la valeur accumulée du compte.
Dans l’exemple précédent, les intérêts étaient composés mensuellement. Nous avons donc pris le taux d’intérêt annuel, généralement appelé taux nominal ou taux annuel en pourcentage (TAP), et l’avons divisé par 12, le nombre de composés dans une année, pour obtenir les intérêts mensuels. L’exposant a ensuite été mesuré en mois.
En généralisant cela, nous pouvons établir une formule générale pour les intérêts composés. Si le TAP est écrit sous forme décimale comme r et qu’il y a k périodes de calcul de l’intérêt composé par année, l’intérêt par période de calcul de l’intérêt composé sera r/k. De même, si nous nous intéressons à la valeur après t années, il y aura kt périodes de calcul de l’intérêt composé dans ce laps de temps.
Formule de calcul des intérêts composés :
Les intérêts composés peuvent être calculés à l’aide de la formule suivante :
![]()
Où :
Si vous investissez 3 000 $ sur un compte de placements rapportant 3 % d’intérêts composés trimestriellement, quelle sera la valeur du compte dans 10 ans?
Puisque nous partons de 3 000 $, a = 3 000.
Notre taux d’intérêt est de 3 %, soit r= 0,03.
Puisque nous calculons l’intérêt composé trimestriellement, nous le calculons quatre fois par année, donc k = 4.
Nous voulons connaître la valeur du compte dans 10 ans, nous cherchons donc A(10), la valeur lorsque t = 10.
![]()
Le compte vaudra 4 045,05 $ dans 10 ans.
Le régime enregistré d’épargne-études (REEE) est un régime d’épargne pour les études postsecondaires dans lequel les parents peuvent investir de l’argent pour payer les frais de scolarité de leurs enfants dans un collège ou une université. Ce compte fructifie à l’abri de l’impôt. Si Lily veut ouvrir un compte REEE pour sa fille, qu’elle souhaite que le compte atteigne 40 000 $ sur 18 ans et qu’elle croit que le compte rapportera 6 % d’intérêts composés semestriellement (deux fois par année), combien Lily devra-t-elle investir dans le compte maintenant?
Comme le compte rapporte 6 %, r = 0,06.
Comme les intérêts sont composés deux fois par année, k = 2.
Dans ce problème, nous ne savons pas avec quelle quantité nous commençons. Nous allons donc résoudre a, la quantité initiale nécessaire. Nous savons que nous voulons que le montant final soit de 40 000 $; nous allons donc chercher la valeur de a pour que A(18) = 40 000.
![]()
![]()
![]()
Lily devra investir 13 801 $ pour disposer de 40 000 $ dans 18 ans.
En raison du calcul de l’intérêt composé tout au long de l’année, l’augmentation réelle au cours d’une année est supérieure au taux de pourcentage annuel. Si 1 000 $ sont investis à 10 %, le tableau ci-dessous indique la valeur après 1 année à différentes fréquences de calcul de l’intérêt composé :
| Fréquence | Valeur après 1 année |
| Annuellement | 1 100 $ |
| Semestriellement | 1 102,50 $ |
| Trimestriellement | 1 103,81 $ |
| Mensuellement | 1 104,71 $ |
| Quotidiennement | 1 105,16 $ |
Le montant gagné s’accroît au fur et à mesure que l’on augmente la fréquence de composition. Remarquez cependant que l’augmentation du calcul de l’intérêt composé annuellement par rapport à semestriellement est plus importante que celle du calcul de l’intérêt composé mensuellement par rapport à quotidiennement. Cela pourrait nous amener à penser que même si l’augmentation de la fréquence du calcul de l’intérêt composé accroît notre résultat, il y a une limite supérieure à ce processus.
Pour s’en convaincre, examinons la valeur de 1 $ placé à un taux d’intérêt de 100 % pendant 1 année.
| Fréquence | Valeur |
| Annuellement | 2 $ |
| Semestriellement | 2,25 $ |
| Trimestriellement | 2,441406 $ |
| Mensuellement | 2,613035 $ |
| Quotidiennement | 2,714567 $ |
| Horaire | 2,718127 $ |
| Chaque minute | 2,718279 $ |
| Chaque seconde | 2,718282 $ |
Ces valeurs semblent en effet s’approcher d’une limite supérieure. Cette valeur est tellement importante qu’elle est représentée par sa propre lettre, un peu comme π représente un nombre.
Nombre d’Euler : e est la lettre utilisée pour représenter la valeur de laquelle ![]() s’approche à mesure que k augmente.
s’approche à mesure que k augmente.
e ≈ 2,718282
Comme e est souvent utilisé comme base d’une exponentielle, la plupart des calculatrices scientifiques disposent d’un bouton qui permet de calculer les puissances de e, généralement appelé ex. Certains logiciels définissent plutôt une fonction exp(x), où exp(x) = ex. Étant donné que e augmente lorsque la période entre les différents calculs de l’intérêt composé est très courte, e nous permet de définir la croissance continue et une nouvelle fonction d’outil, f(x) = ex.
Formule de croissance continue :
La croissance continue peut être calculée à l’aide de la formule suivante :
f(x) = aerx
Où :
Ce type d’équation est couramment utilisé pour décrire des quantités qui changent plus ou moins continuellement, comme les réactions chimiques, la croissance de grandes populations et la désintégration radioactive.
Le radon 222 se désintègre à un taux continu de 17,3 % par jour. Quelle quantité de 100 mg de radon 222 se décomposera en 3 jours?
Étant donné que nous disposons d’un taux de décroissance continu, nous utilisons la formule de croissance continue. Comme la substance se décompose, nous savons que le taux de croissance sera négatif : r = -0,173.
f(3) = 100e-0,173(3) ≈ 59,512 mg de radon 222 est conservé.
1. Supposons qu’une entreprise ait enregistré 50 accidents du travail en 2012 et que le nombre d’accidents déclarés soit passé à 175 en 2018. Si le nombre d’accidents augmente de façon exponentielle, quel est le taux de croissance annuel?
2. Si l’on considère que ces deux équations représentent le solde de deux comptes d’épargne différents, quel compte croît le plus rapidement et quel compte aura un solde plus élevé au bout de trois ans?
3. Une population de 1 000 personnes diminue de 3 % par année. Trouvez la population dans 30 ans.
4. Refaites l’exemple 4.1.8 avec une période de calcul de l’intérêt composé mensuel.
5. La population d’un nid de fourmis est de 225 fourmis, avec un taux de croissance continu de 18 % par semaine. Quelle est la population du nid après 8 semaines?
6. On vous dit que votre carte de hockey vieille de 42 ans vaut 1 200 $. Si cette carte s’apprécie à un taux de 19 % par année, avec le calcul de l’intérêt composé semestriel, quelle était la valeur initiale de la carte?
18
Fonctions logarithmiques
Une population de 50 mouches est censée doubler chaque semaine, ce qui conduit à une fonction de la forme f(x) = 50(2)x, où x représente le nombre de semaines écoulées. Quand cette population atteindra-t-elle 500 individus? Essayer de résoudre ce problème conduit à :
500 = 50(2)x Division des deux côtés par 50 pour isoler la fonction exponentielle.
10 = 2x
Bien que nous ayons établi des modèles exponentiels et que nous les ayons utilisés pour faire des prédictions, vous avez peut-être remarqué que la résolution d’équations exponentielles n’a pas encore été mentionnée. La raison en est simple : aucun des outils algébriques présentés jusqu’à présent n’est suffisant pour résoudre les équations exponentielles. Nous devons introduire une nouvelle fonction, appelée log, qui « défait » une fonction exponentielle, comme une racine carrée « défait » un carré. Les fonctions exponentielles ayant des bases différentes, nous définirons également des logarithmes correspondants ayant des bases différentes.
Logarithme : la fonction logarithmique (base b), soit logb(x), « défait » la fonction exponentielle bx.
L’énoncé ba = c est équivalent à l’énoncé logarithmique b(c) = a.
Puisque la fonction logarithmique et la fonction exponentielle s’annulent l’une l’autre (en termes techniques, ce sont des inverses), il s’ensuit que :
Propriétés logarithmiques : propriétés inverses
logb(bx) = x
blogbx = x
Puisque log est une fonction, il s’écrit plus correctement comme logb(c), avec des parenthèses pour indiquer l’évaluation de la fonction, comme nous le ferions avec f(c). Cependant, lorsque l’entrée est une seule variable ou un seul nombre, il est courant de voir les parenthèses supprimées et l’expression écrite sous la forme logbc.
Écrivez ces équations exponentielles sous forme d’équations logarithmiques :
23 = 8 52 = 25 10-4 = ![]()
23 = 8 est équivalent à log2(8) = 3
52 = 25 est équivalent à log5(25) = 2
10-4 = ![]() est équivalent à log10(
est équivalent à log10(![]() ) = -4
) = -4
En établissant la relation entre les fonctions exponentielles et logarithmiques, nous pouvons maintenant résoudre les équations logarithmiques et exponentielles de base en les réécrivant.
Trouvez la solution de log4(x) = 2 pour x.
Si nous réécrivons cette expression en fonction exponentielle, 42 = x, alors x = 16.
La plupart des calculatrices et des ordinateurs n’évaluent que les logarithmes à deux bases.
Logarithme décimal et logarithme naturel :
Le logarithme décimal est le logarithme en base 10 et s’écrit généralement log(x).
Le logarithme naturel est le logarithme en base e et s’écrit généralement log(x).
Évaluez log(1 000) en utilisant la définition du logarithme décimal.
Pour évaluer log(1 000), nous pouvons dire x = log(1 000), puis le réécrire sous forme exponentielle en utilisant le logarithme décimal en base 10.
10x = 1 000
On peut en déduire que 1 000 est le cube de 10, donc x = 3.
Nous pouvons également utiliser la propriété inverse des logs pour écrire log10(103) = 3.
| Valeurs du logarithme décimal | ||
| Nombre | Nombre comme exponentiel | Log(nombre) |
| 1 000 | 103 | 3 |
| 100 | 102 | 2 |
| 10 | 101 | 1 |
| 1 | 100 | 0 |
| 0,1 | 10-1 | -1 |
| 0,01 | 10-2 | -2 |
| 0,001 | 10-3 | -3 |
Rappelez-vous que la fonction exponentielle f(x) = 2x produit ce tableau des valeurs :
| x | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
| f(x) | 1 | 2 | 4 | 8 |
Étant donné que la fonction logarithmique « défait » la fonction exponentielle, g(x) = log2(x) produit ce tableau des valeurs :
| x | 1 | 2 | 4 | 8 | |||
| f(x) | -3 | -2 | -1 | 0 | 1 | 2 | 3 |
Dans ce deuxième tableau, on remarque que :
En dessinant le graphique, vous remarquerez que lorsque l’entrée s’approche de zéro par la droite, la sortie de la fonction croît très fortement dans la direction négative, ce qui indique une asymptote verticale à x = 0. Une asymptote verticale est une ligne verticale x = a où le graphique tend vers l’infini positif ou négatif lorsque les entrées s’approchent de a.
En représentation symbolique, nous écrivons donc x→0+, f(x)→-∞, et x→∞, f(x)→∞.
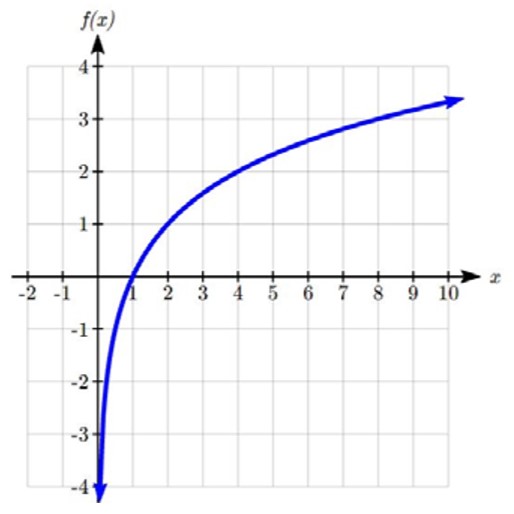
Caractéristiques graphiques du logarithme
Graphiquement, dans la fonction g(x) = logb(x) :
Lorsque l’on dessine un logarithme général de base b, il peut être utile de se rappeler que le graphique passe par les points (1, 0) et (b, 1). Pour avoir une idée de l’influence de la base sur la forme du graphique, examinez les graphiques ci-dessous.
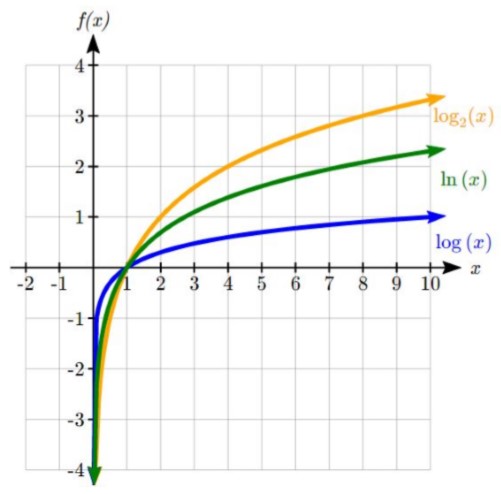
Remarquez que plus la base est grande, plus la croissance du graphique est lente. Par exemple, le graphique logarithmique commun, bien qu’il augmente sans limite, le fait très lentement. Par exemple, pour atteindre un résultat de 8, l’entrée doit être de 100 000 000.
Pour utiliser les fonctions de logarithme décimal ou naturel afin d’évaluer des expressions comme log2(10), nous devons établir quelques propriétés supplémentaires.
Propriétés logarithmiques : Propriété de l’exposant
logb(Ar) = rlogb(A)
Réécrivez log3(25) en utilisant la propriété de l’exposant pour les logarithmes.
Étant donné que 25 = 52 :
log3(25) = log3(52) = 2log35
La deuxième propriété importante permet de changer la base d’une expression logarithmique.
Propriétés logarithmiques : changement de base
![]()
Évaluez log2(10) en utilisant la formule de changement de base.
Selon la formule de changement de base, nous pouvons réécrire le logarithme de base 2 comme un logarithme de n’importe quelle autre base. Comme nos calculatrices peuvent évaluer le logarithme naturel, nous pourrions choisir d’utiliser le logarithme naturel, qui est le logarithme de base e :
![]()
Utilisons nos calculatrices pour évaluer ceci :
![]()
Cela nous permet enfin de répondre à notre question initiale – la population de mouches dont nous avons parlé au début de la section prendra 3,32 semaines pour atteindre 500.
Évaluez log5(100) en utilisant la formule de changement de base.
Nous pouvons réécrire cette expression en utilisant n’importe quelle autre base. Pour ce faire, nous pouvons utiliser le logarithme décimal, en base 10 :
![]()
Une autre approche de la résolution des équations exponentielles est décrite ci-dessous :
Résolution d’équations exponentielles :
Trouvez la solution de 2x = 10 pour x.
En utilisant cette approche alternative, plutôt que de réécrire cette fonction exponentielle sous forme logarithmique, nous prendrons le logarithme des deux côtés de l’équation. Comme nous souhaitons souvent évaluer le résultat à une valeur décimale, nous utiliserons généralement le logarithme décimal ou le logarithme naturel. Pour cet exemple, nous utiliserons le logarithme décimal :
ln(2x) = ln(10) Utilisez la propriété de l’exposant pour les logarithmes.
xln(2) = ln(10) Divisez par ln(2).
x = ![]() ≈ 2,861
≈ 2,861
Remarquez que ce résultat correspond à celui que nous avons obtenu en utilisant la formule de changement de base.
Précédemment, nous avons prédit la population (en milliards) de l’Inde t années après 2008 en utilisant la fonction f(t) = 1,14(1 + 0,0134)t. Si la population continue à suivre cette tendance, quand atteindra-t-elle 2 milliards de personnes?
Nous devons résoudre la valeur de t pour que f(t) = 2 :
| Divisez par 1,14 pour isoler l’expression exponentielle. | |
| Prenez le logarithme des deux côtés de l’équation. | |
| Appliquez la propriété de l’exposant au côté droit. | |
| Divisez les deux côtés par ln(1,0134). |
![]() années
années
Si ce taux de croissance se maintient, le modèle prévoit que la population de l’Inde atteindra 2 milliards de personnes environ 42 ans après 2008, soit approximativement en 2050.
Certaines situations ne peuvent pas être traitées à l’aide des propriétés déjà examinées. Pour cela, nous avons besoin de quelques propriétés supplémentaires :
Propriété de la somme des logarithmes :
![]()
Différence de propriété des logarithmes :
![]()
Grâce à ces propriétés, nous pouvons réécrire des expressions impliquant plusieurs logarithmes en un seul logarithme, ou décomposer une expression impliquant un seul logarithme en expressions impliquant plusieurs logarithmes.
Écrivez log3(5) + log3(8) – log3(2) comme logarithme simple.
Avec la propriété de la somme des logarithmes sur les deux premiers termes :
Cela réduit notre expression originale à log3(40) – log3(2).
Puis, avec la propriété de la différence des logarithmes :
Évaluez 2log(5) + log(4) sans calculatrice en réécrivant d’abord sous la forme d’un seul logarithme.
Pour le premier terme, nous pouvons utiliser la propriété de l’exposant des logarithmes pour écrire :
L’expression étant réduite à une somme de deux logarithmes, log(25) + log(4), nous pouvons utiliser la propriété de la somme des logarithmes :
Comme 100 = 102, nous pouvons évaluer ce logarithme sans calculatrice :
Réécrivez ![]() comme une somme ou une différence de logarithmes.
comme une somme ou une différence de logarithmes.
Tout d’abord, constatant que nous avons un quotient de deux expressions, nous pouvons utiliser la propriété de différence des logarithmes pour écrire :
Puis, en voyant le produit dans le premier terme, nous utilisons la propriété de la somme :
Enfin, nous pourrions utiliser la propriété de l’exposant sur le premier terme :
Les propriétés du logarithme apparaissent souvent lors de la résolution de problèmes impliquant des logarithmes.
Trouvez la solution de ![]() .
.
Afin de réécrire l’équation sous forme exponentielle, nous avons besoin d’une seule expression logarithmique du côté gauche de l’équation. En utilisant la propriété de différence des logarithmes, nous pouvons réécrire le côté gauche :
![]()
La réécriture sous forme exponentielle permet de réduire cette équation à une équation algébrique :
![]()
Solution :
![]()
![]()
![]()
En vérifiant cette réponse dans l’équation originale, nous pouvons nous assurer qu’il n’y a pas de problème de domaine et que cette réponse est bonne.
1. Écrivez l’équation exponentielle 42 = 16 sous forme d’équation logarithmique.
2. Évaluez log(1 000 000).
3. Réécrivez l’équation en utilisant la propriété de l’exposant pour les logarithmes : ln![]() .
.
4. Trouvez la solution de 5(0,93)x = 10.
5. Sans calculatrice, évaluez le résultat en réécrivant d’abord l’équation comme un logarithme simple : log2(8) + log2(4).
6. Trouvez la solution de log(x2 – 4) = 1 + log(x + 2).
7. Supposons que la population de rats dans une ville soit estimée à 1,1 million individus. Si la taille de la population augmente de façon exponentielle à un taux de 15 % par an, combien d’années faudra-t-il pour que la population atteigne 5 millions de rats?
19
Nous avons étudié quelques applications de base des fonctions exponentielles et logarithmiques, mais dans cette section, nous approfondirons certaines applications importantes.
Les équations exponentielles plus complexes peuvent souvent être résolues de plusieurs manières. Dans l’exemple suivant, nous allons résoudre le même problème de deux manières, l’une en utilisant les propriétés de fonctions logarithmiques, l’autre en utilisant les propriétés de fonctions exponentielles.
En 2008, la population du Kenya était d’environ 38,8 millions de personnes et augmentait de 2,64 % par année, tandis que la population du Soudan était d’environ 41,3 millions de personnes et augmentait de 2,24 % par année. Si ces tendances se poursuivent, quand la population du Kenya rejoindra-t-elle celle du Soudan?
Nous commençons par écrire une équation pour chaque population en fonction de t, le nombre d’années après 2008.
Pour savoir quand les populations seront égales, nous pouvons mettre les équations à égalité :
Pour notre première approche, nous prenons le logarithme des deux côtés de l’équation :
En utilisant la propriété de la somme des logarithmes, nous pouvons réécrire chaque côté :
Ensuite, en utilisant la propriété de l’exposant, nous pouvons extraire les variables de l’exposant :
Déplacez tous les termes impliquant t d’un côté de l’équation et le reste des termes de l’autre côté :
Factorisez le t à gauche :
Divisez pour résoudre t :
Solutionnez le problème ci-dessus en réécrivant la formule avant de prendre le logarithme.
Commencez par l’équation :
Divisez pour déplacer les termes exponentiels d’un côté de l’équation et les constantes de l’autre côté :
Utilisez les règles d’exposants pour regrouper à gauche :
Prenez le logarithme des deux côtés :
Utilisez la propriété de l’exposant à gauche :
La division donne :
Bien que la réponse ne semble pas immédiatement identique à celle produite par la méthode précédente, notez qu’avec la propriété de différence des logarithmes, la réponse peut être réécrite :
Bien que les deux méthodes fonctionnent aussi bien l’une que l’autre, il est souvent plus simple d’utiliser l’algèbre avant de prendre les logarithmes, plutôt que de s’appuyer uniquement sur les propriétés des logarithmes.
Dans une section précédente, nous avons traité de la désintégration radioactive – l’idée que les isotopes radioactifs changent au fil du temps. L’un des termes courants associés à la désintégration radioactive est la demi-vie.
Pour l’équation de base de la croissance/décroissance exponentielle h(t) = abt, nous pouvons trouver la demi-vie en solutionnant le moment où il reste la moitié de la quantité originale; en solutionnant ![]() , ou plus simplement
, ou plus simplement ![]() . Remarquez que la quantité initiale n’est pas pertinente lors de la résolution de la demi-vie.
. Remarquez que la quantité initiale n’est pas pertinente lors de la résolution de la demi-vie.
Le bismuth 210 est un isotope qui se désintègre d’environ 13 % par jour. Quelle est la demi-vie du bismuth 210?
On ne nous a pas donné de quantité de départ; nous pouvions donc soit inventer une valeur, soit utiliser une constante inconnue pour représenter la quantité de départ. Pour montrer que la quantité de départ n’influence pas le résultat, désignons la quantité initiale par la constante a. La désintégration du bismuth 210 peut alors être décrite par l’équation Q(d) = a(0,87)d.
Pour trouver la demi-vie, nous voulons déterminer le moment où la quantité restante est égale à la moitié de la quantité originale :![]() . Solution :
. Solution :
| Divisez par a. | |
| Prenez le logarithme des deux côtés. | |
| Utilisez la propriété de l’exposant des logarithmes. | |
| Divisez pour solutionner d. |
Cela nous indique que la demi-vie du bismuth 210 est d’environ 5 jours.
Le césium 137 a une demi-vie d’environ 30 ans. Si vous commencez avec 200 mg de césium 137, quelle quantité restera-t-il après 30 ans? 60 ans? 90 ans?
La demi-vie étant de 30 ans, il ne restera plus que la moitié de la quantité initiale, soit 100 mg, au bout de 30 ans.
Au bout de 60 ans, 30 autres années se seront écoulées, de sorte qu’au cours de cette période, une autre moitié de la substance se sera décomposée, laissant 50 mg.
Après 90 ans, 30 autres années se seront écoulées, de sorte qu’une autre moitié de la substance se sera décomposée, laissant 25 mg.
Le carbone 14 est un isotope radioactif présent dans les matières organiques et couramment utilisé pour la datation d’objets historiques. Le carbone 14 a une demi-vie de 5 730 ans. Si l’on trouve un fragment d’os qui contient 20 % de son carbone 14 d’origine, quel est l’âge de l’os?
Pour déterminer l’âge de l’os, nous devons d’abord trouver une équation pour la désintégration du carbone 14. Nous pourrions utiliser une formule de désintégration continue ou annuelle, mais nous choisissons la formule de désintégration continue, car elle est plus courante dans les textes scientifiques. La demi-vie nous indique qu’après 5 730 ans, il ne reste plus que la moitié de la substance d’origine. Résolution du taux :
| Divisez par a. | |
| Prenez le logarithme naturel des deux côtés. | |
| Utilisez la propriété inverse des logs sur le côté droit. | |
| Divisez par 5 730. |
Maintenant, nous savons que le taux de désintégration suivra l’équation Q(t) = ae-0,000121t. Pour déterminer l’âge du fragment d’os qui contient 20 % de la quantité originale, nous résolvons t, de sorte que Q(t) = 0,20a.
![]()
![]()
![]()
![]()
![]() années
années
Le fragment osseux date donc d’environ 13 300 ans.
Pour les quantités de désintégration, nous avons demandé combien de temps il fallait pour que la moitié de la substance se désintègre. Pour les quantités croissantes, nous pourrions demander combien de temps il faut pour que la quantité double.
Étant donné l’équation de base de la croissance exponentielle h(t) = abt, nous pouvons déterminer le temps de doublement en trouvant le moment où la quantité originale a doublé; en solutionnant 2a = a(b)x, ou plus simplement 2 = bx. Remarquez à nouveau que le montant initial n’est pas pertinent lorsqu’il s’agit de résoudre la question du temps de doublement.
Si vous investissez de l’argent à un taux d’intérêt composé trimestriellement de 8 %, combien de temps faudra-t-il pour que votre argent double?
En utilisant l’équation des intérêts composés, nous pouvons écrire ![]() .
.
Pour trouver le temps de doublement, nous recherchons le temps qui s’écoule jusqu’à ce que nous ayons doublé le montant initial, c’est-à-dire lorsque A(t) = 2P. Remarquez que nous n’avons pas besoin de savoir le montant investi.
![]()
![]()
![]()
![]()
![]() années
années
Il faudra environ 8,75 ans pour que l’investissement double de valeur.
L’utilisation d’un nouveau site Web de réseautage social connaît une croissance exponentielle, le nombre de nouveaux membres doublant tous les cinq mois. Si le site compte actuellement 120 000 utilisateurs et que cette tendance se poursuit, combien d’utilisateurs le site comptera-t-il dans 1 an?
Nous pouvons utiliser le temps de doublement pour trouver une fonction qui modélise le nombre d’utilisateurs du site, puis utiliser cette équation pour répondre à la question. Nous pourrions utiliser un a arbitraire comme nous l’avons fait précédemment pour le montant initial, mais dans ce cas, nous savons que le montant initial est de 120 000.
Si nous utilisons une équation de croissance continue, nous aurons N(t) = 120ert, mesuré en milliers d’utilisateurs après t mois. Sur la base du temps de doublement, il y aurait 240 000 utilisateurs après 5 mois. Cela nous permet de résoudre le problème du taux de croissance continue :
![]()
![]()
![]()
![]()
Nous avons maintenant une équation, N(t) = 120e0,1386t; nous pouvons prédire le nombre d’utilisateurs après 12 mois :
N(12) = 120e0,1386(12) = 633 140 utilisateurs
Au bout de 1 an, le site devrait donc compter environ 633 140 utilisateurs.
1. Le réservoir A contient 10 litres d’eau, et 35 % de l’eau s’évapore chaque semaine. Le réservoir B contient 30 litres d’eau, et 50 % de l’eau s’évapore chaque semaine. Dans combien de semaines les réservoirs contiendront-ils la même quantité d’eau?
2. En 2020, la population du Canada était d’environ 37 742 154 personnes, avec un taux de croissance annuel de 0,89 %. La même année, la population de l’Arabie saoudite était de 34 813 871 personnes, avec un taux de croissance annuel de 1,59 %. Si ces tendances se poursuivent, quand les populations de ces deux pays seront-elles égales?
3. Rappelons que le césium 137 a une demi-vie d’environ 30 ans. Si vous commencez avec 200 mg de césium 137, combien de temps faudra-t-il pour qu’il n’en reste plus que 1 milligramme?
4. Le plutonium 239, produit d’une explosion nucléaire, a une demi-vie de 24 000 ans. Quel pourcentage de plutonium 239 resterait-il après :
5. Si les frais de scolarité dans une université augmentent de 6,6 % chaque année, combien d’années faudra-t-il pour que ces frais doublent?
6. Supposons qu’une nouvelle souche de grippe soit apparue et que le nombre de cas dans le monde double de manière exponentielle tous les sept mois. Quel est le taux de croissance continue (r)?
20
1. ≈ 23,2 %
2. B(t) croît plus rapidement, mais après 3 ans, A(t) a toujours un solde de compte plus élevé
3. 401,0071, ou environ 401 personnes
4. 4 048,06 $
5. ≈ 950 fourmis
6. ≈ 0,59 cents
1. log4(16) = 2
2. 6
3. -2ln(x)
4. ![]()
5. 5
6. 12
7. ≈ 10,8, ou près de 11 ans
1. ≈ 4,1874 semaines
2. ≈ 11,68 ans
3. 229,3157, ou environ 229 ans
4. a. 99,7 %
b. 97,2 %
c. 74,9 %
5. 10,845, ou environ 11 ans
6. ≈ 9,9 %.
V
21
Dans cette section, nous nous familiariserons avec les opérations sur les ensembles et les notations, afin de pouvoir appliquer ces concepts aux problèmes de calcul et de probabilité. Commençons par définir certains termes.
Un ensemble est une collection d’objets dont les membres sont appelés les éléments de l’ensemble. Nous nommons l’ensemble en utilisant des lettres majuscules et nous entourons ses éléments de parenthèses. Supposons que nous devions dresser la liste des membres d’un club d’échecs. Nous utilisons la notation suivante pour les ensembles.
Un ensemble qui n’a pas de membres est appelé un ensemble vide. L’ensemble vide est désigné par le symbole Ø.
Deux ensembles sont égaux s’ils ont les mêmes éléments.
Un ensemble A est un sous-ensemble d’un ensemble B si tout membre de A est également membre de B.
Supposons que C = {Al, Bob, Chris, David, Ed} et que A = {Bob, David}. Alors A est un sous-ensemble de C, soit ![]() .
.
Chaque ensemble est un sous-ensemble de lui-même, et l’ensemble vide est un sous-ensemble de chaque ensemble.
Union de deux ensembles
Si A et B sont deux ensembles, l’union de A et de B, soit ![]() , est l’ensemble de tous les éléments qui sont soit dans A, soit dans B, soit dans A et B à la fois.
, est l’ensemble de tous les éléments qui sont soit dans A, soit dans B, soit dans A et B à la fois.
Intersection de deux ensembles
Si A et B sont deux ensembles, alors l’intersection de A et B, soit ![]() , est l’ensemble de tous les éléments qui sont communs aux deux ensembles A et B.
, est l’ensemble de tous les éléments qui sont communs aux deux ensembles A et B.
Un ensemble universel, U, est l’ensemble composé de tous les éléments considérés.
Complément d’un ensemble
Soit A un ensemble quelconque, alors le complément de l’ensemble A, écrit ![]() , est l’ensemble constitué des éléments de l’ensemble universel U qui ne sont pas dans A.
, est l’ensemble constitué des éléments de l’ensemble universel U qui ne sont pas dans A.
Ensembles disjoints
Deux ensembles A et B sont appelés « ensembles disjoints » si leur intersection est un ensemble vide.
Autrement dit, supposons que l’ensemble universel U représente les couleurs du spectre, et que P, les couleurs primaires. Alors ![]() représente les couleurs du spectre qui ne sont pas des couleurs primaires.
représente les couleurs du spectre qui ne sont pas des couleurs primaires.
Nous utilisons maintenant les diagrammes de Venn pour illustrer les relations entre les ensembles. À la fin des années 1800, un logicien anglais nommé John Venn a mis au point une méthode pour représenter les relations entre les ensembles. Il a représenté ces relations à l’aide de diagrammes, aujourd’hui connus sous le nom de diagrammes de Venn. Un diagramme de Venn représente un ensemble comme l’intérieur d’un cercle. Souvent, deux cercles ou plus sont entourés d’un rectangle qui représente l’ensemble universel. Il est facile de visualiser l’intersection ou l’union d’un ensemble. Dans cette section, nous utiliserons principalement les diagrammes de Venn pour trier diverses populations et compter des objets.
Comme 30 personnes conduisent des voitures à transmission automatique, le cercle A doit contenir 30 éléments. Cela veut dire que x + 12 = 30, ou x = 18. De même, puisque 20 personnes conduisent des voitures à transmission manuelle, le cercle B doit contenir 20 éléments, soit y +12 = 20, ce qui donne y = 8.
Maintenant que toutes les informations sont triées, il est facile de lire sur le diagramme que 18 personnes conduisaient des voitures à transmission automatique uniquement, 12 personnes conduisaient les deux types de voitures et 8 personnes conduisaient des voitures à transmission manuelle uniquement. Par conséquent, 18 + 12 + 8 = 38 personnes ont participé à l’enquête.
Solution
Exercices pratiques1. Soit l’ensemble universel U = {a, b, c, d, e, f, g, h, i, j}, V = {a, e, i, f, h}, et W = {a, c, e, g, i}. Dressez la liste des membres des ensembles suivants : 2. Examinons les ensembles suivants : A = {SRAS, H1N1, H5N1, MERS-CoV, COVID-19, influenza, norovirus}, B = {listériose, Campylobacter, Salmonella, E. coli O157, norovirus, shigella}, et C = {SRAS, listériose, tuberculose, H5N1, Salmonella, VIH, COVID-19}. Dressez la liste des membres des ensembles suivants : 3. Une enquête menée auprès d’athlètes a révélé que pour leurs douleurs légères, 30 utilisaient de l’aspirine, 50 de l’ibuprofène et 15 les deux. Toutes les personnes interrogées ont utilisé au moins l’un des deux analgésiques. Combien d’athlètes ont participé à l’enquête? 4. Une étude menée auprès de 150 étudiant.e.s a révélé que 25 d’entre eux avaient déjà subi une commotion cérébrale ou un traumatisme crânien, que 52 avaient souffert d’une maladie mentale et que 15 avaient connu les deux types de problèmes. Combien d’étudiant.e.s n’ont déclaré aucun des deux résultats? 5. Une enquête menée auprès de 100 étudiant.e.s de l’Université Ryerson révèle que 50 d’entre eux sont abonnés à Netflix, 40 à Amazon Prime et 30 à Disney+. Parmi eux, 15 sont abonnés à la fois à Netflix et à Amazon Prime, 10 à Amazon Prime et à Disney+, 10 à Netflix et à Disney+, et 5 aux trois services. Dessinez un diagramme de Venn et déterminez les éléments suivants :
|
22
Dans ce chapitre, nous essayons de développer des techniques de calcul qui seront utilisées dans les chapitres suivants pour étudier les probabilités. L’une des techniques les plus fondamentales est l’axiome de multiplication. Avant de présenter l’axiome de multiplication, nous allons d’abord voir quelques exemples.
Si un étudiant a deux chemises et trois pantalons qu’il veut porter, combien de tenues différentes composées de ces vêtements peut-il porter?
Solution
Supposons que nous nommions les chemises c1 et c2, et les pantalons p1, p2, et p3. Nous pouvons avoir les six tenues suivantes :
Si un étudiant veut porter deux chemises, trois pantalons et deux paires de chaussures, combien de tenues différentes composées de ces vêtements peut-il porter?
Solution
Supposons que nous nommions les chemises c1 et c2, les pantalons p1, p2 et p3, et les chaussures f1 et f2. Cela se traduit par le schéma en arbre suivant.
Nous comptons le nombre de branches de l’arbre et constatons qu’il y a 12 possibilités différentes. Cette fois-ci, la méthode comporte trois étapes. Tout d’abord, l’étudiant choisit une chemise. Deux choix s’offrent à lui : la première ou la deuxième chemise. Supposons maintenant qu’il choisit la première chemise. Cela nous amène à la deuxième étape du processus, qui consiste à choisir un pantalon. L’étudiant a le choix entre trois pantalons; supposons qu’il choisit le pantalon 2. Maintenant qu’il a choisi une chemise et un pantalon, nous passons à la troisième étape, qui consiste à choisir une paire de chaussures. Comme il a deux paires de chaussures, il a deux choix pour la dernière étape. Supposons qu’il choisit la deuxième paire. Il a choisi la tenue composée d’une chemise, d’un pantalon et de chaussures, soit c1 p2 f2.
En regardant les différentes branches de l’arbre, nous pouvons facilement voir les autres possibilités. Ce qu’il faut retenir ici, c’est qu’il s’agit d’un processus en trois étapes. Pour la première étape du choix d’une chemise, il y a deux possibilités. Pour chaque choix de chemise, il y a trois choix de pantalon, et pour chaque combinaison de chemise et de pantalon, il y a deux choix de chaussures. Au total, nous avons 2 · 3 · 2 = 12 possibilités différentes.
Les schémas en arbre nous aident à visualiser les différentes possibilités, mais ils ne sont pas pratiques lorsque les possibilités sont nombreuses. En outre, nous nous intéressons surtout au nombre d’éléments de l’ensemble, et non aux possibilités réelles. Mais une fois que le problème est envisagé, nous pouvons le résoudre sans schéma en arbre. Les deux exemples que nous venons de résoudre nous ont peut-être donné un indice pour y parvenir. Essayons maintenant de résoudre l’exemple précédent sans schéma en arbre. Rappelons que le problème comportait trois étapes : le choix d’une chemise, le choix d’un pantalon et le choix d’une paire de chaussures. Le nombre de possibilités pour chaque tenue est indiqué ci-dessous.
| Le nombre de possibilités de choisir une chemise | Le nombre de possibilités de choix de pantalons | Le nombre de possibilités de choix de chaussures |
| 2 | 3 | 2 |
En multipliant ces trois nombres, nous obtenons 12, ce qui correspond à ce que nous avons obtenu lorsque nous avons fait le problème à l’aide d’un schéma en arbre. La démarche que nous venons de faire est appelée « axiome de multiplication ».
Axiome de multiplication : si une tâche peut être effectuée de m façons, et une seconde tâche, de n façons, alors l’opération impliquant la première tâche suivie de la seconde peut être effectuée de m · n façons.
L’axiome de multiplication général n’est pas limité à deux tâches et peut être utilisé pour n’importe quel nombre de tâches.
Par conséquent, le nombre de plaques d’immatriculation possibles est de 26 · 10 · 10 · 10 · 10 = 260 000.
En appliquant l’axiome de multiplication, nous obtenons 2 · 2 · 2 = 8 façons différentes.
Par conséquent, six séquences de mots différentes peuvent être formées.
1. Une plaque d’immatriculation se compose de 3 lettres suivies de 3 chiffres. Combien de plaques d’immatriculation sont possibles si aucune lettre ne peut être répétée?
2. Combien de numéros de téléphone à 7 chiffres sont possibles si les 2 premiers chiffres ne peuvent être ni des 1 ni des 0?
3. De combien de façons peut-on répondre par vrai ou faux à un test de 4 questions?
4. De combien de façons différentes peut-on répondre à un examen comportant 8 questions à choix multiples contenant 4 options de réponse et 7 questions de type « vrai ou faux »?
5. Vous souhaitez créer un nouveau mot de passe de 4 chiffres (0 à 9) pour votre téléphone, mais vous ne voulez pas réutiliser le même chiffre plus d’une fois. Combien y a-t-il de possibilités de mots de passe différents?
6. Une serrure à combinaison s’ouvre lorsque vous tournez la roulette d’abord vers la gauche, puis vers la droite, puis à nouveau vers la gauche. S’il y a 30 chiffres sur la roulette, combien y a-t-il de combinaisons possibles?
23
Dans un exemple précédent, on nous a demandé de trouver les séquences de mots formées avec les lettres {A, B, C} si aucune lettre n’est répétée. Le schéma en arbre nous a donné les six arrangements suivants :
ABC, ACB, BAC, BCA, CAB et CBA
Les arrangements de ce type, où l’ordre est important et où aucun élément n’est répété, sont appelés « permutations ».
Il y a quatre choix pour la première lettre de notre mot, trois choix pour la deuxième lettre et deux choix pour la troisième.
| 4 | 3 | 2 |
En appliquant l’axiome de multiplication, nous obtenons 4 · 3 · 2 = 24 arrangements différents.
Le total de permutations est donc 4 · 5 · 4 · 3 · 2 · 1 · 3 = 1 440.
Avant de donner une formule pour nPr, nous allons introduire un symbole que nous utiliserons beaucoup dans ce chapitre ainsi que dans le suivant.
Factoriel : n! = n(n – 1)(n – 2)(n – 3)··· 3 · 2 · 1.
Où n est un nombre naturel.
Cette section portera sur les deux problèmes suivants.
Le premier problème relève de la catégorie des permutations circulaires et le second, des permutations avec des éléments similaires.
Permutations circulaires
Supposons que nous ayons trois personnes appelées A, B et C. Nous avons déjà déterminé qu’elles peuvent être assises en ligne droite de 3! ou 6 façons. Notre prochain problème consiste à déterminer le nombre de façons dont ces personnes peuvent être assises en cercle. Nous dessinons un diagramme :
Il se trouve qu’il n’y a que deux façons de faire asseoir trois personnes en cercle. Ce type de permutation est appelé « permutation circulaire ». Dans ce cas, quelle que soit la place de la première personne, la permutation n’est pas modifiée. Chaque personne peut se déplacer à autant de places qu’elle le souhaite, et la permutation demeurera telle quelle. Imaginez les personnes dans un manège; la rotation de la permutation ne génère pas de nouvelle permutation. Ainsi, dans les permutations circulaires, la première personne détient une place, et l’endroit où elle s’assoit n’a pas d’importance.
Nous rappelons que la première personne peut s’asseoir n’importe où sans modifier la permutation. Il n’y a donc qu’un seul choix pour la première place. Supposons qu’un homme s’assoit en premier. La chaise voisine doit appartenir à une femme, et il y a 4 choix possibles. La chaise suivante doit être occupée par un homme; il y a donc trois choix, et ainsi de suite. Nous énumérons les choix ci-dessous.
| 1 | 4 | 3 | 3 | 2 | 2 | 1 | 1 |
La réponse est 144.
Traitons maintenant du deuxième problème.
Permutations avec des éléments similaires
Déterminons le nombre de permutations possibles des lettres du mot ELEMENT.
Supposons que nous rendions toutes les lettres différentes en les étiquetant comme suit.
Comme toutes les lettres sont maintenant différentes, il y a 7! permutations différentes.
Examinons maintenant une de ces permutations :
Supposons que nous formions de nouvelles permutations à partir de cet arrangement en ne déplaçant que les E. Il est clair qu’il existe 3! ou 6 arrangements de ce type. Nous les énumérons ci-dessous :
1. Un groupe de 15 bénévoles souhaite choisir un.e président.e et un.e secrétaire. De combien de façons différentes peut-on procéder?
2. Combien de permutations des lettres du mot anglais SECURITY se terminent par une consonne?
3. De combien de façons différentes peut-on faire asseoir 5 personnes dans une rangée si 2 d’entre elles insistent pour s’asseoir l’une à côté de l’autre?
4. De combien de façons peut-on disposer sur une étagère 3 livres d’anglais, 3 livres d’histoire et 2 livres de mathématiques, si les livres d’anglais sont placés sur la gauche, les livres d’histoire au milieu et les livres de mathématiques sur la droite?
5. Trouvez le nombre de permutations différentes des lettres du mot MASSACHUSETTS.
6. Si une équipe joue 10 matchs, combien de résultats différents pour 6 victoires et 4 défaites sont possibles?
7. Vous et 6 autres camarades de classe décidez de prendre une photo de groupe en égoportrait.
24
25
1. a. {a, c, e, f, g, h, i}
b. {c, g}
2. a. {SRAS, H5N1, COVID-19}
b. {Tuberculose, VIH}
3. 65
4. 88
5. a. 20
b. 60
c. 10
1. 15 600 000
2. 6 400 000
3. 16
4. 8 388 608
5. 5 040
6. 27 000
1. 210
2. 25 200
3. 48
4. 72
5. 64 864 800
6. 210
7. a. 5 040
b. 720
c. 240
1. 120
2. 2 598 960
3. 20
4. 25
5. a. 4
b. 60
c. 80
6. a. 4 950
b. 17 325
c. 22 737
VI
26
Espaces échantillons et probabilité
Si on tire pile ou face deux fois, quelle est la probabilité d’obtenir face deux fois? Le problème semble simple, mais on entend souvent la mauvaise réponse de ![]() . Un.e étudiant.e peut incorrectement déduire qu’en tirant deux pièces, on pourrait obtenir trois résultats : une face, deux faces, ou aucune face. Ainsi, la probabilité de deux faces serait d’un sur trois. La réponse est incorrecte, car si on tirait pile ou face deux fois, on aurait quatre possibilités, et non trois. Plus précisément, supposez qu’une des pièces est un sous et l’autre est une pièce de cinq cents. Nous avons les quatre possibilités suivantes :
. Un.e étudiant.e peut incorrectement déduire qu’en tirant deux pièces, on pourrait obtenir trois résultats : une face, deux faces, ou aucune face. Ainsi, la probabilité de deux faces serait d’un sur trois. La réponse est incorrecte, car si on tirait pile ou face deux fois, on aurait quatre possibilités, et non trois. Plus précisément, supposez qu’une des pièces est un sous et l’autre est une pièce de cinq cents. Nous avons les quatre possibilités suivantes :
La possibilité FP, par exemple, indique le côté face du sous et le côté pile de la pièce de cinq cents, tandis que PF représente le côté pile du sous et le côté face de la pièce de cinq cents.
C’est pourquoi nous soulignons le besoin de comprendre les espaces échantillons.
On appelle « expérience » l’acte de tirer à pile ou face, de lancer des dés ou de sonder des personnes.
Nous illustrons ces possibilités à l’aide d’un schéma en arbre :
Un des dés étant rouge et l’autre vert, nous avons les 36 possibilités suivantes :
| Vert | ||||||
| Rouge | 1 | 2 | 3 | 4 | 5 | 6 |
| 1 | (1, 1) | (1, 2) | (1, 3) | (1, 4) | (1, 5) | (1, 6) |
| 2 | (2, 1) | (2, 2) | (2, 3) | (2, 4) | (2, 5) | (2, 6) |
| 3 | (3, 1) | (3, 2) | (3, 3) | (3, 4) | (3, 5) | (3, 6) |
| 4 | (4, 1) | (4, 2) | (4, 3) | (4, 4) | (4, 5) | (4, 6) |
| 5 | (5, 1) | (5, 2) | (5, 3) | (5, 4) | (5, 5) | (5, 6) |
| 6 | (6, 1) | (6, 2) | (6, 3) | (6, 4) | (6, 5) | (6, 6) |
Maintenant que nous comprenons le concept d’espace échantillon, nous allons définir la probabilité.
Probabilité : pour un espace échantillon S et un résultat A de S, les deux propriétés suivantes sont satisfaites.
L’exemple que nous venons de voir est composé d’un seul résultat de l’espace échantillon. Nous souhaitons souvent trouver les probabilités de différents résultats représentés par un événement.
Un événement est un sous-ensemble d’un espace échantillon. Si un événement représente seulement un résultat, il s’agit d’un événement simple.
1. Créez un espace échantillon pour l’événement suivant : on lance un dé, et on tire à pile ou face.
2. Une carte est pigée dans un paquet de 52 cartes à jouer. Trouvez les probabilités suivantes :
3. Un bocal contient 6 billes rouges, 7 billes blanches et 7 billes bleues. Si une bille est choisie au hasard, déterminez les probabilités suivantes :
4. On lance 2 dés. Trouvez les probabilités suivantes :
5. Une famille est composée de 4 enfants. Trouvez les probabilités suivantes :
27
28
Dans cette section, nous allons appliquer les techniques de comptage précédemment apprises dans le calcul des probabilités, et utiliser des schémas en arbre pour mieux comprendre la situation.
Commençons par un exemple.
Nous allons maintenant démontrer les résultats ci-dessus avec un schéma en arbre.
On termine la section en résolvant le problème de la date d’anniversaire.
1. On choisit 2 pommes dans un panier contenant 5 pommes rouges et 3 pommes jaunes. Dessinez un schéma en arbre, puis déterminez les probabilités suivantes :
2. Trois billes sont pigées dans un bocal contenant 5 billes rouges, 4 blanches et 3 bleues. Trouvez les probabilités suivantes :
3. Les 4 personnes d’un comité sont choisies parmi un total de 4 étudiant.e.s en santé publique et au travail, 5 en soins infirmiers et 6 en nutrition. Trouvez les probabilités pour les événements suivants :
4. Une équipe de hockey est composée de 2 gardiens de but, 6 joueurs défensifs, 8 ailiers et 4 joueurs de centre. Si l’équipe choisit 5 joueurs de manière aléatoire pour une activité de bienfaisance, trouvez la probabilité des scénarios suivants :
5. Résolvez les problèmes de date d’anniversaire suivants :
29
Supposez que votre ami et vous souhaitez jouer à un jeu qui implique de piger une seule carte dans un paquet bien mélangé. Votre ami vous distribue une carte face cachée du paquet et vous propose ce qui suit : si la carte est un roi, il vous donne 5 $. Sinon, vous lui donnez 1 $. Devriez-vous jouer au jeu?
Voici le raisonnement : puisqu’il y a 4 rois dans un paquet, la probabilité d’obtenir un roi est de 4/52, ou 1/13, et la probabilité de ne pas obtenir de roi est de 12/13. Votre rapport de gains aux pertes est donc de 1 pour 12, tandis que le ratio de rentabilité est de seulement 1 $ pour 5 $. Vous concluez donc que vous ne devriez pas jouer au jeu.
Considérez maintenant le scénario suivant : pendant que votre ami distribuait la carte, vous vous êtes aperçu qu’il s’agissait d’une carte de figure. Devriez-vous maintenant jouer au jeu?
Puisqu’il y a 12 cartes de figure dans le paquet, les éléments totaux dans l’espace échantillon ne sont plus 52, mais seulement 12. Cela signifie que la probabilité d’obtenir un roi est de 4/12, ou 1/3. Votre probabilité de gagner est de 1/3, contre celle de perdre, qui est de 2/3. Cela signifie que votre rapport de gains aux pertes est de 1 pour 2, ce qui est beaucoup mieux que le ratio de rentabilité de 1 $ pour 5 $. Cette fois-ci, vous estimez que vous devriez jouer.
Dans la deuxième partie de l’exemple ci-dessus, nous cherchions la probabilité d’obtenir un roi, sachant que la carte était une figure. Il s’agit d’un exemple de probabilité conditionnelle. Lorsque nous cherchons la probabilité d’un événement E à condition qu’un autre événement F ait lieu, nous cherchons la probabilité conditionnelle.
Le symbole P(E | F) souligne le problème de trouver la probabilité de E étant donné que F a eu lieu. Par P(E | F) on entend « la probabilité de E compte tenu de F ».
Formule de probabilité conditionnelle
Pour 2 événements E et F, la probabilité de E compte tenu de F est :
Les événements H, F, C et V se passent d’explication. Trouvez les probabilités suivantes :
Étant donné que P(F | E) = 0,5, et que P(![]() ) = 0,3, trouvez P(E).
) = 0,3, trouvez P(E).
Solution
En utilisant la formule de probabilité conditionnelle, nous obtenons :
Nous remplaçons :
Supposons que E est l’événement où la famille a 2 garçons et 1 fille, et que F est l’événement où la famille a au moins 2 garçons. Nous voulons trouver P(E | F). Nous énumérons l’espace échantillon, ainsi que les événements E et F :
1. On lance un dé. À l’aide de la formule à cet effet, trouvez la probabilité conditionnelle qu’un 3 s’affiche si on sait qu’un nombre impair s’est affiché.
2. Le tableau suivant montre la distribution de personnes buvant du café, par sexe :
| Boivent du café | Hommes (H) | Femmes (F) | TOTAL |
| Oui (O) | 31 | 33 | 64 |
| Non (N) | 19 | 17 | 36 |
| 50 | 50 | 100 |
Utilisez le tableau pour déterminer les probabilités suivantes :
3. Dans le programme de la santé publique et au travail de l’Université Ryerson, 60 % des étudiant.e.s passent le cours de biostatistique, 70 %, le cours de droit de l’environnement et 30 %, les deux cours. Si un étudiant est choisi au hasard, déterminez les probabilités suivantes :
4. Considérez une famille de 3 enfants. Quelle est la probabilité que la famille ait des enfants des deux sexes, étant donné que le premier né est un garçon?
5. Si P(![]() ) = 0,25 et que P(F | E) = 0,55, trouvez P(E).
) = 0,25 et que P(F | E) = 0,55, trouvez P(E).
6. Un sondage a été réalisé auprès des conducteur.trice.s pour déterminer le nombre de contraventions pour excès de vitesse qui ont été reçues parmi les hommes et les femmes. Les données sont affichées dans le tableau ci-dessous.
| Nombre de contraventions | Hommes (H) | Femmes (F) | Total |
| 0 | 425 | 600 | 1 025 |
| 1 | 250 | 175 | 425 |
| 2 | 125 | 75 | 200 |
| 3 | 100 | 50 | 150 |
| Total | 900 | 900 | 1 800 |
Utilisez le tableau pour déterminer les probabilités suivantes :
30
![]() = {FFP},
= {FFP}, ![]()
1. Dans un sondage auprès de 100 personnes, 40 boivent occasionnellement, et 60 ne boivent pas. Parmi les personnes qui boivent, 10 ont des maux de tête faibles. Parmi les personnes qui ne boivent pas, 5 ont des maux de tête faibles. Est-ce que les événements « boivent » et « ont des maux de tête » sont indépendants?
2. Supposons que 80 % des personnes attachent leur ceinture de sécurité et que 5 % des personnes ont arrêté de fumer l’année dernière. Si 4 % des personnes qui attachent leur ceinture de sécurité arrêtent de fumer, les événements « attachent leur ceinture de sécurité » et « arrêtent de fumer » sont-ils indépendants?
3. Si ![]() ,
, ![]() et E et F sont indépendants, trouvez
et E et F sont indépendants, trouvez ![]() .
.
4. Les probabilités que John et Linda passent le cours de gestion des données sont de 40 % et de 70 % respectivement. Si les deux événements sont indépendants, trouvez les probabilités suivantes :
5. Le tableau ci-dessous montre la distribution des employé.e.s dans une entreprise qui ont signalé un accident au travail selon leurs années d’expérience de travail au sein de cette entreprise.
| Moins de 10 ans d’expérience (M) | 10 ans d’expérience ou plus (E) | Total | |
| N’a pas signalé d’accident au travail (N) | 300 | 100 | 400 |
| A signalé un accident au travail (O) | 150 | 50 | 200 |
| 450 | 150 | 600 |
6. Étant donné que ![]() ,
, ![]() , si A et B sont indépendants, trouvez
, si A et B sont indépendants, trouvez ![]() .
.
31
1. {1F, 2F, 3F, 4F, 5F, 6F, 1P, 2P, 3P, 4P, 5P, 6P}
2. a. ![]()
b. ![]()
3. a. ![]()
b. ![]()
4. a. ![]()
b. ![]()
5. a. ![]()
b. ![]()
1. a. Non
b. Oui
c. Non
2. ![]()
3. 40 %
4. a. ![]()
b. ![]()
5. 0,5
6. a. 0,375
b. 0,55
c. 0,175
1. a. ![]()
b. ![]()
2. a. ![]()
b. ![]()
3. a. ![]()
b. ![]()
c. ![]()
4. a. 0,0036
b. 0,1291
c. 0,0619
d. 0,4474
5. a. 0,8831
b. 0,9704
1. ![]()
2. a. ![]()
b. ![]()
c. ![]()
3. a. ![]()
b. ![]()
4. ![]()
5. ![]()
6. a. ![]()
b. ![]()
c. ![]()
1. Non
2. Oui
3. 0,36
4. a. ![]()
b. ![]()
5. a. ![]()
b. ![]()
c. ![]()
d. Oui
6. 0,50
VII
32
Probabilité binomiale
Dans cette section, nous allons examiner les types de problèmes qui impliquent une séquence d’épreuves, où chaque épreuve a seulement deux résultats possibles : le succès ou l’échec. Ces épreuves sont indépendantes. Cela dit, le résultat d’une épreuve n’influence pas le résultat d’une autre épreuve. Par ailleurs, la probabilité de succès, p, et la probabilité d’échec (1 – p), demeurent les mêmes tout au long de l’expérience. On appelle ces problèmes des problèmes de probabilité binomiale. Puisqu’ils ont été étudiés par un mathématicien suisse nommé Jacques Bernoulli aux alentours des années 1700, ils sont également connus sous le nom d’épreuves de Bernoulli.
Ceci nous amène à la définition suivante :
Expérience binomiale : une expérience binomiale satisfait aux quatre conditions suivantes :
Le modèle de probabilité que nous allons étudier nous fournit les outils pour résoudre de nombreux problèmes de la vie réelle comme ceux énumérés ci-dessous.
Considérons maintenant l’exemple suivant pour élaborer une formule afin de trouver la probabilité de k succès dans n épreuves de Bernoulli.
Cela nous donne le théorème suivant :
Théorème de la probabilité binomiale :
On trouve la probabilité d’obtenir k succès en n épreuves de Bernoulli indépendantes de la manière suivante :
où p indique la probabilité de succès, et q = (1 – p), la probabilité d’échec.
Nous utilisons la formule ci-dessus pour résoudre les exemples suivants :
1. Quelle est la probabilité d’obtenir 3 fois 1 si on lance un dé 5 fois?
2. Un joueur de basketball a 80 % de chance de marquer un panier lors d’un lancer franc. Sur 5 lancers francs, quelle est la probabilité qu’il marque :
3. Si un médicament guérit 75 % des personnes qui le prennent, quelle est la probabilité que parmi les 30 personnes qui le prennent :
4. L’Agence canadienne d’inspection des aliments (ACIA) a constaté que 5 % des épices importées au Canada étaient contaminées par des bactéries pathogéniques d’origine alimentaire. Quelle est la probabilité qu’un lot de 25 épices importées ait :
5. Un cadre a déterminé que, dans le cadre d’une initiative de don de porte-à-porte, 20 % des ménages visités fourniront un don. Si on visite 10 ménages, quelle est la probabilité qu’au plus 2 d’entre eux fournissent un don?
33
Dans cette section, nous étudierons la formule de Bayes pour résoudre un type de problème important en probabilité. La formule de Bayes est une méthode de calcul de la probabilité conditionnelle P(F | E) à partir de P(E | F). Les idées présentées ici ne sont pas nouvelles, et la majorité de ces problèmes se résout à l’aide d’un schéma en arbre. Toutefois, la formule de Bayes offre un outil pour résoudre ces problèmes sans schéma en arbre. Commençons par un exemple.
Disons que CI représente le fait que le contenant I est choisi, que CII représente que le contenant II est choisi, que N représente le fait qu’une bille noire est pigée et que B représente le fait qu’une bille blanche est pigée. Illustrons cette situation à l’aide d’un schéma en arbre.
| Voici une proposition de la formule de Bayes. Formule de Bayes :Disons que S est un espace d’échantillon divisé en n parties, A1, A2, . . . An. Si E représente un événement dans S, alors :
Pour certains problèmes, il est possible d’utiliser une approche beaucoup plus intuitive que la formule de Bayes.
Exercices pratiques1. Le contenant I contient cinq billes rouges et trois billes blanches, alors que le contenant II contient quatre billes rouges et deux billes blanches. Un contenant est choisi au hasard et une bille y est pigée. Dessinez le schéma en arbre, puis déterminez les probabilités suivantes : 2. Le tableau ci-dessous résume les résultats d’un test de diagnostic :
À l’aide du tableau, calculez ce qui suit : 3. Une entreprise d’ordinateurs achète ses puces électroniques de trois fabricants différents. Le fabricant I fournit 60 % des puces, dont 5 % sont défectueuses. Le fabricant II fournit 30 % des puces, dont 4 % sont défectueuses. Le reste des puces est fourni par le fabricant III, dont 3 % sont défectueuses. Si une puce électronique est choisie au hasard, déterminez les probabilités suivantes : 4. Le tableau suivant montre le pourcentage « d’accréditations conditionnelles » reçues par différents services alimentaires d’une ville au cours de leur dernière inspection de la santé publique.
Si un lieu est choisi au hasard, déterminez les probabilités suivantes :
|
34
Une valeur probable est une perte ou un gain prévus dans un jeu de hasard. Le concept de valeur probable est fortement lié à la moyenne pondérée. Étudions les situations suivantes.
Dans la première situation, pour trouver la valeur probable, nous avons multiplié chaque résultat par la probabilité de son occurrence, puis nous avons calculé la somme des montants calculés pour tous les cas possibles. Dans le second exemple, si nous considérons la note du questionnaire comme étant un résultat, nous faisions le même calcul. Cela nous amène donc à la définition suivante.
Valeur probable : Si une expérience dispose de la distribution de probabilité suivante,
| Résultat | x1 x2 x3 ··· xn |
| Probabilité | p(x1) p(x2) p(x3) ··· p(xn) |
Donc, en moyenne, il y a 1,56 enfant par famille.
Disons que D représente l’événement où la porte est déverrouillée et que V représente l’événement où la porte reste verrouillée. Illustrons cette situation à l’aide d’un schéma en arbre.
|
Exercices pratiques1. Dans un pays européen, 20 % des familles ont trois enfants, 40 % ont deux enfants, 30 % ont un enfant et 10 % des familles n’ont aucun enfant. En moyenne, combien y a-t-il d’enfants par famille? 2. Un centre communautaire local prévoit amasser des fonds en faisant tirer une carte cadeau de 500 $. Au total, 3 000 billets sont vendus au prix de 1 $. Déterminez la valeur probable du prix pour une personne qui achète un billet pour le tirage. 3. Un billet de loterie de 1 $ donne la possibilité de gagner un grand prix de 10 000 $, 10 prix de 1 000 $ chacun, 100 prix de 100 $ chacun ainsi que 1 000 prix de 10 $ chacun. Déterminez la valeur probable d’une participation au concours si 1 million de billets sont vendus. 4. Dans un jeu, il faut piger une seule carte d’un jeu standard de 52 cartes. La personne reçoit 75 cents pour un as, 25 cents pour un roi et 5 cents pour une carte rouge qui n’est ni un as, ni un roi. Si le coût de chaque pige est de 15 cents, quelle est la valeur probable de ce jeu? 5. Un joueur de basketball a 80 % de chance de marquer un panier lors d’un lancer franc. S’il marque un panier au premier lancer, il a 90 % de chance de réussir le second. Toutefois, s’il manque son premier lancer, il n’a que 70 % de chance de réussir le second. S’il a droit à deux lancers francs, quelle est la probabilité qu’il en réussisse au moins un? 6. Un dé est lancé jusqu’à ce que le chiffre un (1) soit obtenu. Quelle est la probabilité d’obtenir le chiffre 1 en quatre lancers ou moins? 7. Vous oubliez de régler votre réveil 60 % du temps. Si vous entendez votre réveil, vous l’éteignez et vous vous rendormez 20 % du temps. Même si vous vous levez à temps, vous commencez à vous préparer en retard environ 30 % du temps. Selon ces circonstances, quelle est la probabilité que vous arriviez en retard à votre cours du matin? 8. Votre ami souhaite devenir un courtier immobilier agréé en Ontario. Le taux de réussite de l’examen est d’environ 60 %. Si une personne échoue à l’examen, son taux de réussite augmente à environ 70 % lors du deuxième essai, puis à 75 % lors du troisième essai. Quelle est la probabilité que votre ami réussisse son examen en trois essais ou moins?
|
35
Chaînes de Markov
Nous étudierons maintenant les processus aléatoires, des expériences pendant lesquelles les résultats des événements dépendent des résultats précédents. Un tel processus ou une telle expérience se nomme une chaîne de Markov ou un processus de Markov. Le processus a été étudié pour la première fois au début des années 1900 par un mathématicien russe nommé Andrei A. Markov.
Une petite ville est desservie par deux compagnies de téléphone, Maman Bell et Papa Bell. En raison de tactiques de vente persuasives, chaque mois, 40 % de la clientèle de Maman Bell passent aux services de Papa Bell, c’est-à-dire que les 60 % restants de la clientèle restent avec Maman Bell. D’un autre côté, 30 % de la clientèle de Papa Bell passent aux services de Maman Bell. Les renseignements précédents s’expriment à l’aide d’une matrice qui énumère les probabilités de passer d’un état à un autre. Cette matrice se nomme la matrice de transition.
Il faut noter qu’une matrice de transition est toujours une matrice carrée, puisque tous les états possibles doivent avoir des rangées et des colonnes. Tous les intrants d’une matrice de transition ne sont pas négatifs puisqu’ils représentent des probabilités. De plus, puisque tous les résultats possibles sont considérés comme étant dans le processus de Markov, la somme des intrants par rangée est toujours de 1.
Disons que M représente le fait que le professeur Symons marche et que V représente le fait qu’il prend son vélo. Nous utilisons le schéma en arbre suivant pour calculer les probabilités.
| Lundi | Mardi | Mercredi |
Certaines chaînes de Markov, nommées chaînes de Markov régulières, ont tendance à se stabiliser à long terme. La matrice utilisée dans les exemples ci-haut s’avère être une de ces chaînes de Markov. Le prochain exemple traite de la tendance à long terme ou de la situation à l’état stable pour cette matrice.
Lorsque cela survient, nous disons que le système est à un état stable ou à un état d’équilibre. Dans cette situation, tous les vecteurs de rangée sont équivalents. Si la matrice d’origine est une matrice n sur n, nous obtenons n vecteurs qui sont tous pareils. Nous appelons ce vecteur un vecteur à probabilité fixe ou le vecteur d’équilibre E. Dans le problème ci-dessus, le vecteur à probabilité fixe E est ![]() . De plus, si le vecteur d’équilibre E est multiplié par la matrice d’origine T, le résultat est le vecteur d’équilibre E. Soit :
. De plus, si le vecteur d’équilibre E est multiplié par la matrice d’origine T, le résultat est le vecteur d’équilibre E. Soit :
Chaînes de Markov régulières
Une chaîne de Markov atteint un état d’équilibre s’il s’agit d’une chaîne de Markov régulière. Une chaîne de Markov est dite régulière si une partie de sa puissance n’a que des intrants positifs.
Lorsque nous utilisons des puissances plus élevées de T, Tn, et que n devient plus gros, nous approchons d’un état d’équilibre. Le vecteur de répartition de l’équilibre E se trouve en déterminant que ET = E.
![]() et
et ![]()
Le vecteur d’équilibre E peut-il être trouvé sans développer la matrice de transition aux puissances élevées? La réponse à cette question nous donne une manière de trouver le facteur d’équilibre E. La réponse se trouve dans le fait que ET = E. Puisque nous avons la matrice T, nous pouvons déterminer E à partir de l’énoncé ET = E. L’exemple suivant illustre cette approche.
1. Un sondage auprès des gens qui achètent des voitures américaines détermine que, si une personne achète une voiture Ford, il y a 60 % de chances que la prochaine voiture qu’elle achète soit une voiture Ford. Toutefois, les propriétaires de voitures GM achèteront une voiture GM à nouveau selon une probabilité de 0,80. Représentez les habitudes d’achat de ces personnes dans une matrice de transition.
2. Un joueur de hockey décide de lancer la rondelle (L) ou de la passer à un coéquipier (P) selon la matrice de transition suivante.
Déterminez ce qui suit :
3. Le service de police local lance une campagne pour réduire les taux de textos envoyés au volant dans la communauté. Les effets de la campagne sont résumés dans la matrice de transition ci-dessous :
Si 35 % des personnes dans la communauté rapportent avoir envoyé des textos au volant avant la campagne :
4. Une grande entreprise mène un programme de formation auprès de son personnel afin de réduire le nombre de fois où une personne qui glisse, trébuche ou tombe sur son lieu de travail. Environ 15 % du personnel a signalé avoir glissé, trébuché ou fait une chute au cours de l’année précédente (an 1). Après le programme de formation (an 2), 75 % des personnes ayant précédemment signalé un accident n’en ont pas signalé d’autres, alors que 5 % de ceux qui n’avaient pas signalé d’accident en ont signalé un cette année.
36
1. 0,0322
2. a. 0,0064
b. 0,2048
c. 0,9424
3. a. 0,1047
b. 0,0604
c. 0,0269
d. 0,2026
4. a. 0,3650
b. 0,2305
5. 0,6778
1. a. 0,6458
b. 0,4706
c. 0,625
2. a. 0,125
b. 0,7241
3. a. 0,045
b. 0,2667
c. 0,03
4. a. 0,0572
b. 0,07
c. 0,0446
1. 1,7
2. -0,83 cents
3. -0,96 cents
4. -0,0519 cents
5. 0,94
6. 0,5177
7. 0,776
8. 0,97
1.
2. a. 0,32
b. Lancer (L) = ![]() , Passe (P) =
, Passe (P) = ![]()
3. a. 31 %
b. 25 %
4 . a.
b. 680
c. 561
d. 6,25 %